河南省中考数学真题模拟题分类卷3 坐标与函数综合(近几年)
试卷更新日期:2021-08-25 类型:二轮复习
一、单选题
-
1. 已知抛物线 经过 和 两点,则n的值为( )A、﹣2 B、﹣4 C、2 D、42. 如图1,矩形 中,点 为 的中点,点 沿 从点 运动到点 ,设 , 两点间的距离为 , ,图2是点 运动时 随 变化的关系图象,则 的长为( )
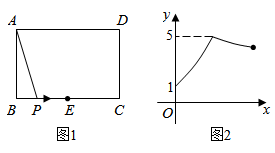 A、4 B、5 C、6 D、73. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、4. 如图,在 中, .边 在x轴上,顶点 的坐标分别为 和 .将正方形 沿x轴向右平移当点E落在 边上时,点D的坐标为( )
A、4 B、5 C、6 D、73. 若点 在反比例函数 的图像上,则 的大小关系为( )A、 B、 C、 D、4. 如图,在 中, .边 在x轴上,顶点 的坐标分别为 和 .将正方形 沿x轴向右平移当点E落在 边上时,点D的坐标为( ) A、 B、 C、 D、5. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( )
A、 B、 C、 D、5. 如图,在 中,顶点 , , ,将 与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转 ,则第70次旋转结束时,点D的坐标为( ) A、 B、 C、 ) D、6. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( )
A、 B、 C、 ) D、6. 如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于 DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为( ) A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)7. 如图,正方形 的顶点 , 的坐标分别为 , .若正方形 第 次沿 轴翻折,第2次沿 轴翻折,第 3次沿 轴翻折,第4次沿 轴翻折,第5次沿 轴翻折,…,则第 次翻折后点 对应点的坐标为( )
A、( ﹣1,2) B、( ,2) C、(3﹣ ,2) D、( ﹣2,2)7. 如图,正方形 的顶点 , 的坐标分别为 , .若正方形 第 次沿 轴翻折,第2次沿 轴翻折,第 3次沿 轴翻折,第4次沿 轴翻折,第5次沿 轴翻折,…,则第 次翻折后点 对应点的坐标为( ) A、 B、 C、 D、8. 如图,点 在反比例函数 的图象上,点 在反比例函数 的图象上,且 轴, 于点 ,交 轴于点 .若 的面积为3,则 的值为( )
A、 B、 C、 D、8. 如图,点 在反比例函数 的图象上,点 在反比例函数 的图象上,且 轴, 于点 ,交 轴于点 .若 的面积为3,则 的值为( ) A、-3 B、-2 C、2 D、39. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A、-3 B、-2 C、2 D、39. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )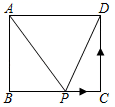 A、
A、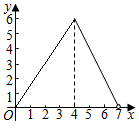 B、
B、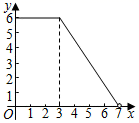 C、
C、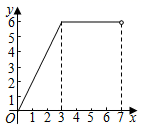 D、
D、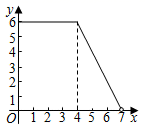 10. 若点A(﹣2,y1),B(﹣1,y2)在反比例函数y= 的图象上,则y1﹣y2的值为( )A、负数 B、0 C、正数 D、无法确定11. 如图,在正方形ABCD中,顶点A,B,C,D在坐标轴上,且B(4,0),以AB为边构造菱形ABEF,将菱形ABEF与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转45°,则第164次旋转结束时,点 的坐标为( )
10. 若点A(﹣2,y1),B(﹣1,y2)在反比例函数y= 的图象上,则y1﹣y2的值为( )A、负数 B、0 C、正数 D、无法确定11. 如图,在正方形ABCD中,顶点A,B,C,D在坐标轴上,且B(4,0),以AB为边构造菱形ABEF,将菱形ABEF与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转45°,则第164次旋转结束时,点 的坐标为( ) A、(﹣4,4 ) B、(﹣4,﹣4 ) C、(4 ,﹣4) D、(﹣4 ,﹣4)12. 某同学在平面直角坐标系内设计了一个动点运动的编程.若一个动点从点 出发,沿 …运动,则点 的坐标为( )A、 B、 C、 D、13. 如图,在矩形ABCD中,AB=8,BC=6,点P从点B出发沿线段BC向点C运动,线段AP的垂直平分线分别交AB,DC于点M,N,设BM=y,BP=x,则y与x之间的函数图象大致是( )
A、(﹣4,4 ) B、(﹣4,﹣4 ) C、(4 ,﹣4) D、(﹣4 ,﹣4)12. 某同学在平面直角坐标系内设计了一个动点运动的编程.若一个动点从点 出发,沿 …运动,则点 的坐标为( )A、 B、 C、 D、13. 如图,在矩形ABCD中,AB=8,BC=6,点P从点B出发沿线段BC向点C运动,线段AP的垂直平分线分别交AB,DC于点M,N,设BM=y,BP=x,则y与x之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 14. 在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表:
14. 在二次函数y=-x2+bx+c中,函数y与自变量x的部分对应值如下表:x
……
-2
0
3
4
……
y
……
-7
m
n
-7
……
则m、n的大小关系为( )
A、m>n B、m<n C、m=n D、无法确定15. 如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到正方形的边时的点为P1(2,0),第2次碰到正方形的边时的点为P2 , …,第n次碰到正方形的边时的点为Pn , 则点P2018的坐标是( ) A、(1,4) B、(4,3) C、(2,4) D、(4,1)16. 对于二次函数y=﹣x2﹣4x+5,以下说法正确的是( )A、x<﹣1时,y随x的增大而增大 B、x<﹣5或x>1时,y>0 C、A(﹣4,y1),B( ,y2)在y=﹣x2﹣4x+5的图象上,则y1<y2 D、此二次函数的最大值为817. 如图,在平面直角坐标系中,四边形ABCD是菱形,AB∥x轴,点B的坐标为(4,1),∠BAD=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形ABCD的两边分别交于点M,N(点N在点M的上方),连接OM,ON,若△OMN的面积为s,直线l的运动时间为t秒(0≤t≤6),则S与t的函数图象大致是( )
A、(1,4) B、(4,3) C、(2,4) D、(4,1)16. 对于二次函数y=﹣x2﹣4x+5,以下说法正确的是( )A、x<﹣1时,y随x的增大而增大 B、x<﹣5或x>1时,y>0 C、A(﹣4,y1),B( ,y2)在y=﹣x2﹣4x+5的图象上,则y1<y2 D、此二次函数的最大值为817. 如图,在平面直角坐标系中,四边形ABCD是菱形,AB∥x轴,点B的坐标为(4,1),∠BAD=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形ABCD的两边分别交于点M,N(点N在点M的上方),连接OM,ON,若△OMN的面积为s,直线l的运动时间为t秒(0≤t≤6),则S与t的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
18. 请写出一个图象经过原点的函数的解析式.
三、综合题
-
19. 如图,大、小两个正方形的中心均与平面直角坐标系的原点O重合,边分别与坐标轴平行,反比例函数 的图象与大正方形的一边交于点A(1,2),且经过小正方形的顶点B.
 (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.20. 如图,抛物线 与直线 交于点A(2,0)和点 .
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.20. 如图,抛物线 与直线 交于点A(2,0)和点 .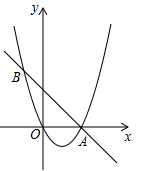 (1)、求 和 的值;(2)、求点 的坐标,并结合图象写出不等式 的解集;(3)、点 是直线 上的一个动点,将点 向左平移 个单位长度得到点 ,若线段 与抛物线只有一个公共点,直接写出点 的横坐标 的取值范围.21. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
(1)、求 和 的值;(2)、求点 的坐标,并结合图象写出不等式 的解集;(3)、点 是直线 上的一个动点,将点 向左平移 个单位长度得到点 ,若线段 与抛物线只有一个公共点,直接写出点 的横坐标 的取值范围.21. 暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠;
设某学生暑期健身x(次),按照方案一所需费用为 ,(元),且 ;按照方案二所需费用为 (元) ,且 其函数图象如图所示.
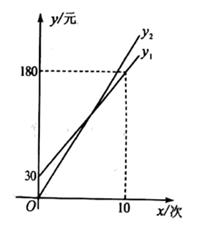 (1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.22. 如图,抛物线 与x轴正半轴,y轴正半轴分别交于点 ,且 点G为抛物线的顶点.
(1)、求 和b的值,并说明它们的实际意义;(2)、求打折前的每次健身费用和 的值;(3)、八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.22. 如图,抛物线 与x轴正半轴,y轴正半轴分别交于点 ,且 点G为抛物线的顶点. (1)、求抛物线的解析式及点G的坐标;(2)、点 为抛物线上两点(点M在点N的左侧) ,且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点 之间(含点 )的一个动点,求点Q的纵坐标 的取值范围.23. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)、求抛物线的解析式及点G的坐标;(2)、点 为抛物线上两点(点M在点N的左侧) ,且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点 之间(含点 )的一个动点,求点Q的纵坐标 的取值范围.23. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: (1)、建立函数模型
(1)、建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得 ,即 ;由周长为m,得 ,即 .满足要求的 应是两个函数图象在第象限内交点的坐标.
(2)、画出函数图象函数 的图象如图所示,而函数 的图象可由直线 平移得到.请在同一直角坐标系中直接画出直线 .
(3)、平移直线 ,观察函数图象①当直线平移到与函数 的图象有唯一交点 时,周长m的值为;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)、得出结论若能生产出面积为4的矩形模具,则周长m的取值范围为.
24. 某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系关于销售单价,日销售量,日销售利润的几组对应值如表:销售单价x(元)
85
95
105
115
日销售量y(个)
175
125
75
m
日销售利润w(元)
875
1875
1875
875
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)、求y关于x的函数解析式(不要求写出x的取值范围)及m的值;(2)、根据以上信息,填空:该产品的成本单价是元,当销售单价x=元时,日销售利润w最大,最大值是元;
(3)、公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
25. 如图,反比例函数y= (x>0)的图象过格点(网格线的交点)P.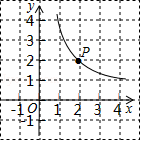 (1)、求反比例函数的解析式;(2)、在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:
(1)、求反比例函数的解析式;(2)、在图中用直尺和2B铅笔画出两个矩形(不写画法),要求每个矩形均需满足下列两个条件:①四个顶点均在格点上,且其中两个顶点分别是点O,点P;
②矩形的面积等于k的值.
26. 如图,抛物线 与 轴交于点 ,与 轴交于点 ,点 是线段 上方的抛物线上的动点,过点 作 轴交 于点 . (1)、求抛物线的解析式;(2)、当线段 的长取得最大值时,连接 , .请判断四边形 的形状并说明理由.27. 如图①,在△ABC中,∠ACB=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED并延长交CG于点F,连接AF.设A、E两点间的距离为xcm,E、F两点间的距离为ycm.小亮根据学习函数的经验,对因变量y随自变量x变化而变化的规律进行了探究.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)下面是小亮的探究过程,请补充完整:
(1)、求抛物线的解析式;(2)、当线段 的长取得最大值时,连接 , .请判断四边形 的形状并说明理由.27. 如图①,在△ABC中,∠ACB=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED并延长交CG于点F,连接AF.设A、E两点间的距离为xcm,E、F两点间的距离为ycm.小亮根据学习函数的经验,对因变量y随自变量x变化而变化的规律进行了探究.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.)下面是小亮的探究过程,请补充完整: (1)、列表:如表的已知数据是根据A、E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:
(1)、列表:如表的已知数据是根据A、E两点间的距离x进行取点、画图、测量,分别得到了x与y的几组对应值:x/cm
0
1
2
3
4
5
6
y/cm
9.49
7.62
5.83
3.16
3.16
4.24
请你通过计算补全表格;
(2)、描点、连线:在平面直角坐标系xOy中,描出剩余的点(x,y),并画出函数y关于x的图象;(3)、根据函数图象,当E、F两点间的距离y最小时,A、E两点间的距离约为cm;(4)、解决问题:当EF﹣AE=2时,BE的长度大约是cm.(结果保留1位小数)28. 如图,抛物线y=ax2﹣4x+c经过点A(2,﹣2),且当x=1时,函数y有最小值.(如需作图或作辅助线,请先将原题草图画在对应题目的答题区域后再作答.) (1)、求抛物线的解析式;(2)、点B的坐标为(﹣3,﹣4),点B关于原点的对称点为B',点C是抛物线对称轴上一动点,若抛物线在直线BB'下方的部分与直线BC有公共点,求点C纵坐标yc的取值范围.29. 如图,直线 与双曲线 相交于 、 两点,直线 与 轴相交于点 ,点 的坐标是 , , 为 轴正半轴上一点,且 .
(1)、求抛物线的解析式;(2)、点B的坐标为(﹣3,﹣4),点B关于原点的对称点为B',点C是抛物线对称轴上一动点,若抛物线在直线BB'下方的部分与直线BC有公共点,求点C纵坐标yc的取值范围.29. 如图,直线 与双曲线 相交于 、 两点,直线 与 轴相交于点 ,点 的坐标是 , , 为 轴正半轴上一点,且 . (1)、双曲线 的解析式是 , 直线 的解析式是.(2)、求证: .(3)、当 时, 的取值范围是.30. 如图所示,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于点C,A,以AC为边在第一象限内作正方形ABDC,点B在双曲线y= (k≠0)第一象限内的一支上.
(1)、双曲线 的解析式是 , 直线 的解析式是.(2)、求证: .(3)、当 时, 的取值范围是.30. 如图所示,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别交于点C,A,以AC为边在第一象限内作正方形ABDC,点B在双曲线y= (k≠0)第一象限内的一支上. (1)、求反比例函数的解析式;(2)、将正方形沿x轴正方向平移m个单位长度后,点D恰好落在该双曲线上,求m.31. 如图,反比例函数y= (x<0)的图象过格点(网格线的交点)P.(1)、求反比例函数的解析式;(2)、在图中用直尺和2B铅笔画出两个三角形(不写画法),要求每个三角形均需满足下列两个条件:
(1)、求反比例函数的解析式;(2)、将正方形沿x轴正方向平移m个单位长度后,点D恰好落在该双曲线上,求m.31. 如图,反比例函数y= (x<0)的图象过格点(网格线的交点)P.(1)、求反比例函数的解析式;(2)、在图中用直尺和2B铅笔画出两个三角形(不写画法),要求每个三角形均需满足下列两个条件:①三个顶点均在格点上,且其中两个顶点分别是点O,点P;
②三角形的面积等于|k|的值.
 32. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,一次函数与坐标轴交于C,D两点,且点C,D是线段 的三等分点, .
32. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,一次函数与坐标轴交于C,D两点,且点C,D是线段 的三等分点, . (1)、求一次函数与反比例函数的解析式;(2)、求 的面积.33. 某电子厂商投产一种新型电子产品,每件制造成本为16元,每月销售量y(万件)与销售单价x(元)之间的函数关系如下表所示:
(1)、求一次函数与反比例函数的解析式;(2)、求 的面积.33. 某电子厂商投产一种新型电子产品,每件制造成本为16元,每月销售量y(万件)与销售单价x(元)之间的函数关系如下表所示:销售单价x(元)
…
25
30
35
40
…
每月销售量y(万件)
…
50
40
30
20
…
(1)、求每月销售量y(万件)与销售单价x(元)之间的函数关系式;(2)、设每月的利润为W(万元)当销售单价为多少元时,厂商每月获得的总利润为480万元?(3)、如果厂商每月的制造成本不超过480万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?34. 如图,抛物线 交x轴于A,B两点,交y轴于点C.直线 经过点A,C.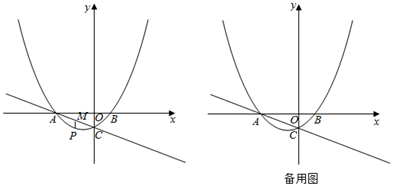 (1)、求抛物线的解析式;(2)、点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
(1)、求抛物线的解析式;(2)、点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.①当 是直角三角形时,求点P的坐标;
②作点B关于点C的对称点 ,则平面内存在直线l,使点M,B, 到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线 的解析式.(k,b可用含m的式子表示)
35. 如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C. (1)、求抛物线的解析式;(2)、过点A的直线交直线BC于点M.
(1)、求抛物线的解析式;(2)、过点A的直线交直线BC于点M.①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.
36. 如图1,在 中 , , .点 是以 为直径的半圆上的动点,设 , 两点间的距离为 , , 两点间的距离为 , , 两点间的距离为 .根据学习函数的经验,小宇分别对函数 , 随自变量 的变化而变化的规律进行了探究.下面是小宇的探究过程,请补充完整:(1)、根据点 在半圆上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值:0
1
2
3
3.5
2
3
3.8
4.4
4
3.5
3.3
2.8
1.7
0
如图2,在平面直角坐标系 中,画出了函数 的图象,请在同一坐标系中,描点并画出函数 的图象;
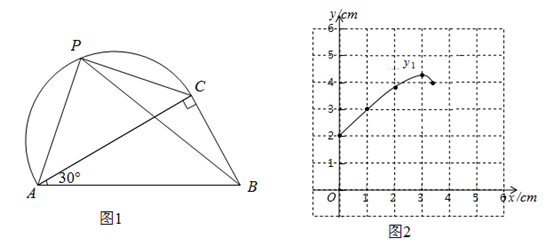 (2)、结合函数图象填空:当 时, ;当 时, 的取值范围是___;(结果精确到 )(3)、当 时,结合函数图象写出线段 与 的长.(结果精确到 )37. 已知抛物线 与 轴交于 、 两点(点 在点 的左边),与 轴交于点 ,抛物线的顶点为 ,连接 、 , .(1)、求抛物线的顶点 的坐标.(2)、求证: ,(3)、点 在抛物线上,点 在直线 上,是否存在点 、 使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.38. 如图,抛物线y=﹣ x2+bx+c与x轴交于点A(4,0),与y轴交于点B,且OA=OB,在x轴上有一动点D(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E,
(2)、结合函数图象填空:当 时, ;当 时, 的取值范围是___;(结果精确到 )(3)、当 时,结合函数图象写出线段 与 的长.(结果精确到 )37. 已知抛物线 与 轴交于 、 两点(点 在点 的左边),与 轴交于点 ,抛物线的顶点为 ,连接 、 , .(1)、求抛物线的顶点 的坐标.(2)、求证: ,(3)、点 在抛物线上,点 在直线 上,是否存在点 、 使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.38. 如图,抛物线y=﹣ x2+bx+c与x轴交于点A(4,0),与y轴交于点B,且OA=OB,在x轴上有一动点D(m,0)(0<m<4),过点D作x轴的垂线交直线AB于点C,交抛物线于点E, (1)、求抛物线的函数表达式.(2)、当点C是DE的中点时,求出m的值.(3)、在(2)的条件下,将线段OD绕点O逆时针旋转得到OD′,旋转角为α(0°<a<90°),连接D′A、D′B,直接写出D′A+ D′B的最小值.
(1)、求抛物线的函数表达式.(2)、当点C是DE的中点时,求出m的值.(3)、在(2)的条件下,将线段OD绕点O逆时针旋转得到OD′,旋转角为α(0°<a<90°),连接D′A、D′B,直接写出D′A+ D′B的最小值.
-