河南省中考数学真题模拟题分类卷2 方程与不等式（近几年）

试卷更新日期：2021-08-25 类型：二轮复习

进入出卷网下载

一、单选题

1. 国家统计局统计数据显示，我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为（）

A、 $5000 (1 + 2 x) = 7500$ B、 $5000 \times 2 (1 + x) = 7500$ C、 $5000 {(1 + x)}^{2} = 7500$ D、 $5000 + 5000 (1 + x) + 5000 {(1 + x)}^{2} = 7500$

查看试题解析
2. 一元二次方程 $(x + 1) (x - 1) = 2 x + 3$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
3. 2020年，我国国内生产总值达到101.6万亿元，数据“101.6万亿”用科学记数法表示为（）

A、 10.16×10¹³ B、0.1016×10¹⁵ C、1.016×10¹² D、1.016×10¹⁴

查看试题解析
4. 若方程 $x^{2} - 2 x + m = 0$ 没有实数根，则 $m$ 的值可以是（）

A、-1 B、 $0$ C、1 D、 $\sqrt{3}$

查看试题解析
5. 定义运算： $m ☆ n = m n^{2} - m n - 1$ .例如 $: 4 ☆ 2 = 4 \times 2^{2} - 4 \times 2 - 1 = 7$ .则方程 $1 ☆ x = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根

查看试题解析
6. 《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，还差3钱，问合伙人数、羊价各是多少？设合伙人数为x人，羊价为y钱，根据题意，可列方程组为（）

A、 ${\begin{matrix} \end{matrix} \begin{matrix} y = 5 x + 45 \\ y = 7 x + 3 \end{matrix}$ B、 ${\begin{matrix} \end{matrix} \begin{matrix} y = 5 x - 45 \\ y = 7 x + 3 \end{matrix}$ C、 ${\begin{matrix} \end{matrix} \begin{matrix} y = 5 x + 45 \\ y = 7 x - 3 \end{matrix}$ D、 ${\begin{matrix} \end{matrix} \begin{matrix} y = 5 x - 45 \\ y = 7 x - 3 \end{matrix}$

查看试题解析
7. 下列一元二次方程中，有两个不相等实数根的是（）

A、x²+6x+9=0 B、x²=x C、x²+3=2x D、（x﹣1）²+1=0

查看试题解析
8. 不等式组 ${\begin{matrix} 2 - x \leq 5 \\ \frac{x + 3}{2} < 1 \end{matrix}$ 的最大整数解是（）

A、-3 B、-2 C、-1 D、0

查看试题解析
9. 近年来，“快递业”成为我国经济的一匹“黑马”，2017年我国快递业务量为400亿件，2019年快递量将达到600亿件，设快递量平均每年增长率为x，则下列方程中正确的是（）

A、400（1+x）＝600 B、400（1+2x）＝600 C、400（1+x）²＝600 D、600（1﹣x）²＝400

查看试题解析
10. 关于x的一元二次方程x（x+1）﹣3＝mx的根的情况是（）

A、无实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断

查看试题解析
11. 将4个数 $a$ 、 $b$ 、 $c$ 、 $d$ 排成2行、2列，两边各加一条竖直线记成 $| \begin{array}{l} a & b \\ c & d \end{array} |$ ，定义 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ .例如 $| \begin{array}{l} 8 & 9 \\ 3 & 5 \end{array} | = 8 \times 5 - 9 \times 3 = 40 - 27 = 13$ .则方程 $| \begin{array}{l} x & 1 \\ 6 x & x \end{array} | = - 9$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
12. 不等式组 ${\begin{array}{l} - x + 3 < x - 5 \\ x > m + 1 \end{array}$ 的解集是 $x > 4$ ，那么m的取值范围是（）

A、 $m = 3$ B、 $m \geq 3$ C、 $m < 3$ D、 $m \leq 3$

查看试题解析
13. 某中学组织全区优秀九年级毕业生参加学校冬令营，一共有x名学生，分成y个学习小组.若每组10人，则还差5人；若每组9人，还余下3人.若求冬令营学生的人数，所列的方程组为（）

A、 ${\begin{array}{l} 10 x = y + 5 \\ 9 x = y - 3 \end{array}$ B、 ${\begin{array}{l} 10 y = x - 5 \\ 9 y = x + 3 \end{array}$ C、 ${\begin{array}{l} 10 y = x + 5 \\ 9 y = x - 3 \end{array}$ D、 ${\begin{array}{l} 10 x = y - 5 \\ 9 x = y + 3 \end{array}$

查看试题解析
14. 关于 $x$ 的一元二次方程 $k x^{2} - 4 x + 1 = 0$ 有两个实数根，则 $k$ 的取值范围是（）

A、 $k > 4$ B、 $k ⩽ 4$ C、 $k < 4$ 且 $k \neq 0$ D、 $k ⩽ 4$ 且 $k \neq 0$

查看试题解析

二、填空题

15. 不等式组 ${\begin{array}{l} 2 x + 10 \geq 0 \\ \frac{x}{2} + 3 < 6 \end{array}$ 的解集为.

查看试题解析
16. 不等式组 ${\begin{array}{l} \frac{x}{2} ⩽ - 1 \\ - x + 7 > 4 \end{array}$ 的解集是.

查看试题解析
17. 不等式组 ${\begin{matrix} x + 5 > 2 \\ 4 - x \geq 3 \end{matrix}$ 的最小整数解是．

查看试题解析
18. 若关于x的一元二次方程 $\frac{1}{2} x^{2} + 3 x - m = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是．

查看试题解析
19. 关于 $x$ 的不等式组 ${\begin{array}{l} - 3 x - 6 < 0 \\ 2 x - a < 3 \end{array}$ 的解集在数轴上如图表示，则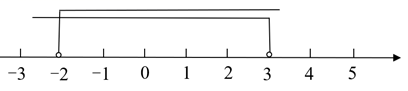 $a$ 的值为.

查看试题解析
20. 不等式组1＜ $\frac{1}{2}$ x﹣2≤2的所有整数解的和为.

查看试题解析
21. 若关于x的一元二次方程 $2 m x^{2} - 3 x + 1 = 0$ 有两个不相等的实数根，则实数m的取值范围是.

查看试题解析

三、综合题

22. 猕猴嬉戏是王屋山景区的一大特色，猕猴玩偶非常畅销.小李在某网店选中 $A$ ， $B$ 两款猕猴玩偶，决定从该网店进货并销售.两款玩偶的进货价和销售价如下表：

类别

价格

$A$ 款玩偶

$B$ 款玩偶

进货价（元/个）

40

30

销售价（元/个）

56

45

(1)、第一次小李用1100元购进了 $A$ ， $B$ 两款玩偶共30个，求两款玩偶各购进多少个；

(2)、第二次小李进货时，网店规定 $A$ 款玩偶进货数量不得超过 $B$ 款玩偶进货数量的一半.小李计划购进两款玩偶共30个，应如何设计进货方案才能获得最大利润，最大利润是多少？

(3)、小李第二次进货时采取了（2）中设计的方案，并且两次购进的玩偶全部售出，请从利润率的角度分析，对于小李来说哪一次更合算？
（注：利润率 $= \frac{利润}{成本} \times 100 %$ ）

查看试题解析
23. 学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元.

(1)、求A，B两种奖品的单价；

(2)、学校准备购买A，B两种奖品共30个，且A奖品的数量不少于B奖品数量的 $\frac{1}{3}$ .请设计出最省钱的购买方案，并说明理由.

查看试题解析
24. 为预防新冠病毒，某大型商场积极响应政府号召，除对进入商场人员进行体温测量、督促戴口罩外，每天还对商场全面消毒．经了解，该商场购买的是 $A$ ， $B$ 两种桶装消毒液，已知2桶 $A$ 种消毒液和3桶 $B$ 种消毒液共需要1200元； $5$ 桶 $A$ 种消毒液和1桶 $B$ 种消毒液共需要1700元．

(1)、求 $A$ ， $B$ 两种消毒液每桶的单价；

(2)、政府规定：若该商场一次购买 $A$ 种消毒液30桶以上，买几桶每桶补贴几元(每桶最多补贴100元)； $B$ 种消毒液没有补贴．若该商场一次购买两种消毒液共100桶，且 $A$ 种消毒液桶数不少于 $B$ 种消毒液桶数的 $\frac{2}{3}$ ，则商场最少要花多少钱?

查看试题解析
25. 为提升校园体育运动多样性，助力师生“阳光运动”，某校决定采购一批排球和足球，小明在某体育用品商店咨询了排球和足球的售价具体信息：购买2个排球和3个足球共需460元，购买12个排球所需费用与购买5个足球所需费用相同.

(1)、求排球和足球的售价分别是多少元？

(2)、若该校计划购进排球和足球共100个，其中排球的数量不超过足球的3倍，请设计出最省钱的购买方案，并说明理由.

查看试题解析
26. 某超市每天能销售河南特产“伊川富硒小米”和“伊川贡小米”共21袋（5斤装），且“伊川富硒小米”6天销售的袋数与“伊川贡小米”8天销售的袋数相同.

(1)、该超市每天销售“伊川富硒小米”和“伊川贡小米”各多少袋？

(2)、“伊川富硒小米”每袋进价20元，售价25元；“伊川贡小米”每袋进价30元，售价33元.若超市打算购进“伊川富硒小米”和“伊川贡小米”共80袋，其中“伊川富硒小米”不超过40袋，要求这80袋小米全部销售完后的总利润不少于316元，则该超市如何购进这两种小米获利最大？最大利润是多少元？

查看试题解析
27. 某市中招体育测试改革，其中篮球和足球作为选考项目，某商店抓住这一商机决定购进一批篮球和足球共200个，这两种球的进价和售价如下表所示：

篮球

足球

进价（元/个）

180

150

售价（元/个）

250

200

(1)、若商店计划销售完这批球后能获利11600元，问篮球和足球应分别购进多少个？

(2)、设购进篮球 $x$ 个，获利为 $y$ 元，求 $y$ 与 $x$ 之间的函数关系；

(3)、若商店计划投入资金不多于31560元且销售完这批球后商店获利不少于11000元，请问有哪几种购球方案，并写出获利最大的购球方案.

查看试题解析
28. 书法是中华民族的文化瑰宝，是人类文明的宝贵财富，是我国基础教育的重要内容.某学校准备为学生的书法课购买一批毛笔和宣纸，已知购买40支毛笔和100张宣纸需要280元；购买30支毛笔和200张宣纸需要260元.

(1)、求毛笔和宣纸的单价；

(2)、某超市给出以下两种优惠方案：
方案 $A$ ：购买一支毛笔，赠送一张宣纸；

方案 $B$ ：购买200张宣纸以上，超出的部分按原价打八折，毛笔不打折.学校准备购买毛笔50支，宣纸若干张（超过200张），选择哪种方案更划算？请说明理由.

查看试题解析

29. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，如表是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	4台	1200元
第二周	5台	6台	1900元

（进价、售价均保持不变，利润＝销售收入﹣进货成本）

(1)、求A、B两种型号的电风扇的销售单价；

(2)、若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？

(3)、在（2）的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

查看试题解析

	篮球	足球
进价（元/个）	180	150
售价（元/个）	250	200