湘教版数学九年级上册同步训练《1.2 反比例函数的图像与性质》
试卷更新日期:2021-08-25 类型:同步测试
一、单选题
-
1. 若点A(1,3)在反比例函数y 的图象上,则k的值是( )A、1 B、2 C、3 D、42. 如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为 的函数图象.根据这个函数的图象,下列说法正确的是( )
 A、图象与 轴没有交点 B、当 时 C、图象与 轴的交点是 D、 随 的增大而减小3. 在同一直角坐标系中,函数 与 的大致图象是( )
A、图象与 轴没有交点 B、当 时 C、图象与 轴的交点是 D、 随 的增大而减小3. 在同一直角坐标系中,函数 与 的大致图象是( )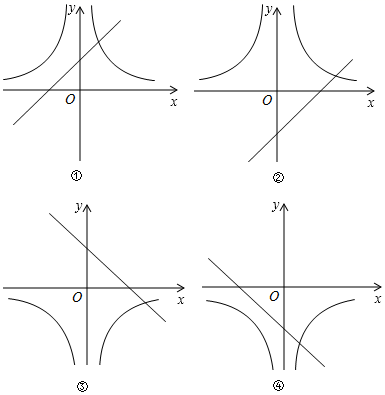 A、①② B、②③ C、②④ D、③④4. 已知反比例函数 的图象与正比例函数 的图象相交于 两点,若点 的坐标是 ,则点 的坐标是( )A、 B、 C、 D、5. 根据反比例函数的性质、联系化学学科中的溶质质量分数的求法以及生活体验等,判定下列有关函数 (a为常数且 )的性质表述中,正确的是( )
A、①② B、②③ C、②④ D、③④4. 已知反比例函数 的图象与正比例函数 的图象相交于 两点,若点 的坐标是 ,则点 的坐标是( )A、 B、 C、 D、5. 根据反比例函数的性质、联系化学学科中的溶质质量分数的求法以及生活体验等,判定下列有关函数 (a为常数且 )的性质表述中,正确的是( )①y随x的增大而增大;②y随x的增大而减小;③ ;④
A、①③ B、①④ C、②③ D、②④6. 下列说法正确的是( )A、函数 的图象是过原点的射线 B、直线 经过第一、二、三象限 C、函数 ,y随x增大而增大 D、函数 ,y随x增大而减小7. 如图,在同一平面直角坐标系中,直线y=t(t为常数)与反比例函数y1 ,y2 的图象分别交于点A,B,连接OA,OB,则△OAB的面积为( )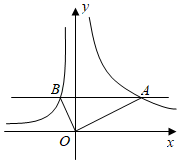 A、5t B、 C、 D、58. 已知反比例函数y (k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A、5t B、 C、 D、58. 已知反比例函数y (k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )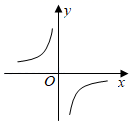 A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限9. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、410. 一次函数 与反比例函数 的图象交于点 ,点 .当 时,x的取值范围是( )A、 B、 或 C、 D、 或
A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限9. 一次函数 的图象与x轴交于点B,与反比例函数 的图象交于点 ,且 的面积为1,则m的值是( )A、1 B、2 C、3 D、410. 一次函数 与反比例函数 的图象交于点 ,点 .当 时,x的取值范围是( )A、 B、 或 C、 D、 或二、填空题
-
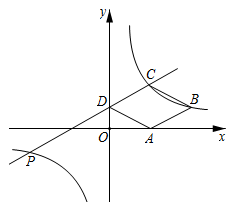
11. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.
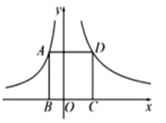 12. 如图,若反比例函数 的图象经过等边三角形POQ的顶点P,则△POQ的边长为.
12. 如图,若反比例函数 的图象经过等边三角形POQ的顶点P,则△POQ的边长为.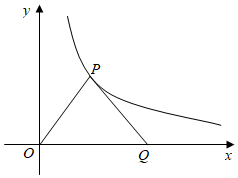 13. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.
13. 如图,直线 与反比例函数 的图象交于A,B两点,与x轴交于点C,且 ,连接OA.已知 的面积为12,则k的值为.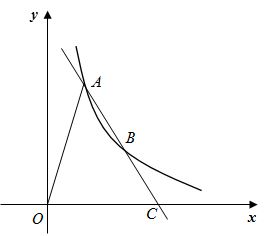 14. 如图,矩形 的顶点 在反比例函数 的图象上,矩形 的面积为3,则 ;
14. 如图,矩形 的顶点 在反比例函数 的图象上,矩形 的面积为3,则 ; 15. 已知点A为直线y=-2x上一点,过点A作 轴,交双曲线 于点B . 若点A与点B关于y轴对称,则点A的坐标为 .16. 如图,点 在反比例函数 的图象上,点M在x轴的正半轴上,点N在y轴的负半轴上,且 .点 是线段 上一动点,过点A和P分别作x轴的垂线,垂足为点D和E,连接 、 .当 时,x的取值范围是.
15. 已知点A为直线y=-2x上一点,过点A作 轴,交双曲线 于点B . 若点A与点B关于y轴对称,则点A的坐标为 .16. 如图,点 在反比例函数 的图象上,点M在x轴的正半轴上,点N在y轴的负半轴上,且 .点 是线段 上一动点,过点A和P分别作x轴的垂线,垂足为点D和E,连接 、 .当 时,x的取值范围是.
三、解答题
-
17. 如图,在平面直角坐标系中.四边形 为矩形,点 、 分别在 轴和 轴的正半轴上,点 为 的中点已知实数 ,一次函数 的图象经过点 、 ,反比例函数 的图象经过点 ,求 的值.
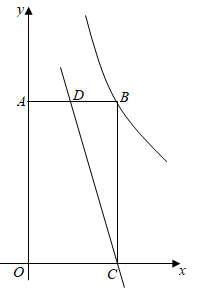 18. 如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.
18. 如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.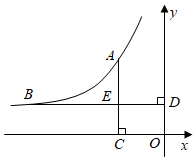 (1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).19. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,若 .
(1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).19. 如图,一次函数 的图象与反比例函数 的图象交于点 ,与 轴交于点 ,过点 作 轴,垂足为 ,若 .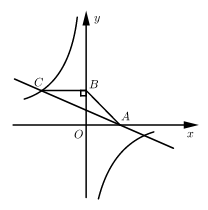 (1)、求点 的坐标及 的值;(2)、若 ,求一次函数的表达式.20. 如图,一次函数y=x+2的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.
(1)、求点 的坐标及 的值;(2)、若 ,求一次函数的表达式.20. 如图,一次函数y=x+2的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.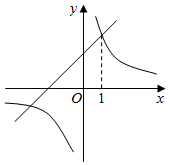 (1)、求k的值;(2)、若将一次函数y=x+2的图象向下平移4个单位长度,平移后所得到的图象与反比例函数 的图象相交于A,B两点,求此时线段AB的长.
(1)、求k的值;(2)、若将一次函数y=x+2的图象向下平移4个单位长度,平移后所得到的图象与反比例函数 的图象相交于A,B两点,求此时线段AB的长.