湘教版数学九年级上册同步训练《1.1 反比例函数》

试卷更新日期：2021-08-24 类型：同步测试

进入出卷网下载

一、单选题

1. 下列函数中，y是x的反比例函数的是（）

A、 $y = \frac{1}{2 x}$ B、 $y = - \frac{1}{x^{2}}$ C、 $y = \frac{1}{x + 3}$ D、 $y = 2 + \frac{1}{x}$

查看试题解析
2. 在下列函数中，y是x的反比例函数的是(　　)

A、y＝x－1 B、y＝ $\frac{8}{x^{2}}$ C、y＝－2x^－1 D、 $\frac{y}{x}$ ＝2

查看试题解析
3. 某物体对地面的压力为定值，物体对地面的压强 $P (P a)$ 与受力面积 $S (m^{2})$ 之间的函数关系如图所示，这一函数表达式为（）

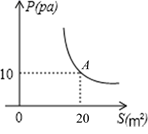A、 $P = \frac{20}{S}$ B、 $P = \frac{200}{S}$ C、 $S = \frac{20}{P}$ D、 $S = \frac{200}{P}$

查看试题解析
4. 下列关系式中，y是x的反比例函数的是（）

A、y＝4x B、 $\frac{y}{x}$ ＝3 C、y＝﹣ $\frac{1}{x}$ D、y＝x²﹣1

查看试题解析
5. 2020年益阳始建高铁站，该站建设初期需要运送大量的土石方，某运输公司承担了运送总量为 $10^{6} m^{3}$ 土石方的任务，该运输公司平均运送土石方的速度 $v$ （单位： $m^{3}$ /天）与完成运送任务所需的时间 $t$ （单位：天）之间的函数关系式是（）

A、 $v = \frac{10^{6}}{t}$ B、 $v = 10^{6}$ C、 $v = \frac{1}{10^{6}} t^{2}$ D、 $v = 10^{6} t^{2}$

查看试题解析
6. 下列函数：① $y = x - 2$ ，② $y = \frac{3}{x}$ ，③ $y = x^{2}$ ，④ $y = x^{2} + 3 x + 4$ ， $y$ 是 $x$ 的反比例函数的个数有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即：阻力 $\times$ 阻力臂=动力 $\times$ 动力臂.小伟欲用撬棍撬动一块石头，已知阻力和阻力臂分别是 $1500 N$ 和 $0.4 m$ ，则动力F （单位： N）关于动力臂L（单位： $m$ ）的函数解析式正确的是（）

A、 $F = \frac{1500}{L}$ B、 $F = \frac{700}{L}$ C、 $F = \frac{600}{L}$ D、 $F = \frac{0.4}{L}$

查看试题解析
8. 下列数表中分别给出了变量y与x的几组对应值，其中是反比例函数关系的是（）

A、

$x$

1

2

3

4

$y$

7

8

9

10

B、

$x$

1

2

3

4

$y$

3

6

9

12

C、

$x$

1

2

3

4

$y$

1

0.5

$\frac{1}{3}$

0.25

D、

$x$

1

2

3

4

$y$

4

3

2

1

查看试题解析
9. 购买 $x$ 斤水果需 $24$ 元，购买一斤水果的单价 $y$ 与 $x$ 的关系式是（）

A、 $y = \frac{24}{x} (x > 0)$ B、 $y = \frac{24}{x}$ （ $x$ 为自然数） C、 $y = \frac{24}{x}$ （ $x$ 为整数） D、 $y = \frac{24}{x}$ （ $x$ 为正整数）

查看试题解析
10. 若 $y = \frac{m (m - 3)}{x}$ 是反比例函数，则m满足的条件是（）

A、m≠0 B、m=3 C、m=3或m=0 D、m≠3且m≠0

查看试题解析

二、填空题

11. 某工程队为教学楼贴瓷砖，已知楼体外表面积为5×10³m².所需的瓷砖块数n与每块瓷砖的面积S（单位：m²）的函数关系式为.

查看试题解析
12. 已知圆柱的体积是30cm² ，它的高h（单位：cm）关于底面面积S（单位：cm²）的函数解析式为.

查看试题解析
13. 已知函数 $y = (m - 2) x^{| m | - 3}$ 是反比例函数，则 $m =$ .

查看试题解析
14. 某高速公路全长为 $200 k m$ ，那么汽车行完全程所需的时间 $t (h)$ 与行驶的平均速度 $V (k m / h)$ 之间的关系式为．

查看试题解析
15. 已知直线y＝﹣x+1与双曲线y＝﹣ $\frac{4}{x}$ （x＞0）交于点M（m ， n），则代数式 $\frac{1}{m}$ + $\frac{1}{n}$ 的值是．

查看试题解析
16. 验光师测的一组关于近视眼镜的度数y与镜片的焦距x的数据，如表：
y（单位：度）
100
200
400
500
…
x（单位：米）
1.00
0.50
0.25
0.20
…
则y关于x的函数关系式是．

查看试题解析

三、解答题

17. 设面积为 $20 c m^{2}$ 的平行四边形的一边长为 $a c m$ ，这条边上的高为 $h c m$ ．求 $h$ 关于 $a$ 的函数解析式(写出自变量 $a$ 的取值范围)并求当 $h = 5$ 时， $a$ 的值．

查看试题解析
18. 已知 $y = y_{1} + y_{2}$ ， $y_{1}$ 与 $x$ 成正比例， $y_{2}$ 与 $x$ 成反比例，且当x=1时， y=-1，当x=3时，y=5 ，求y与x之间的函数关系式.

查看试题解析
19. 已知一个长方体的体积是100cm³ ，它的长是ycm，宽是10cm，高是xcm．
（1）写出y与x之间的函数关系式；
（2）当x=2cm时，求y的值．

查看试题解析
20. 将x= $\frac{2}{3}$ 代入反比例函数y=﹣ $\frac{1}{x}$ 中，所得函数值记为y₁ ，又将x=y₁+1代入函数中，所得函数值记为y₂ ，再将x=y₂+1代入函数中，所得函数值记为y₃…如此继续下去，求y₂₀₁₄的值．

查看试题解析
21. 面积一定的梯形，其上底长是下底长的 $\frac{1}{3}$ ，设上底长为xcm，高为ycm，且当x=5cm，y=6cm，

(1)、求y与x的函数关系式；

(2)、求当y=4cm时，下底长多少？

查看试题解析
22.
某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种，下图是某天恒温系统从开启到关闭及关闭后，大棚内温度y（℃）随时间x（小时）变化的函数图象，其中BC段是双曲线y= $\frac{k}{x}$ 的一部分．请根据图中信息解答下列问题：
（1）恒温系统在这天保持大棚内温度18℃的时间有多少小时？
（2）求k的值；
（3）当x=18时，大棚内的温度约为多少度？

查看试题解析

y（单位：度）	100	200	400	500	…
x（单位：米）	1.00	0.50	0.25	0.20	…

$x$	1	2	3	4
$y$	7	8	9	10

$x$	1	2	3	4
$y$	3	6	9	12

$x$	1	2	3	4
$y$	1	0.5	$\frac{1}{3}$	0.25

$x$	1	2	3	4
$y$	4	3	2	1