初中数学北师大版七年级上册期末检测B卷
试卷更新日期:2021-08-24 类型:期末考试
一、单选题
-
1. 下面的说法正确的是( )A、 是多项式 B、 表示负数 C、 的系数是 D、-2是单项式2. 如果|a|=3,|b|=1,且a>b,那么a+b的值是( )A、4 B、2 C、﹣4 D、4或23. 把如图所示的正方形展开,得到的平面展开图可以是( )
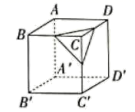 A、
A、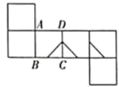 B、
B、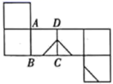 C、
C、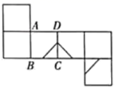 D、
D、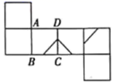 4. 若 , , ,则 , , , 这四个数的大小关系是( )A、 B、 C、 D、5. 一种商品,降价10%后的售价是 元,则原价为( )A、 元 B、 元 C、 元 D、 元6. 下列采用的调查方式中,不合适的是( )A、了解永安溪的水质,采用抽样调查 B、检测神舟十二号飞船的零部件质量,采用抽样调查 C、了解我县中学生视力情况,采用抽样调查 D、了解某班同学的数学成绩,采用全面调查7. 按规律排列的一组数据: , ,□, , , ,…,其中□内应填的数是( )A、 B、 C、 D、8. 线段AB的长为2cm,延长AB到C,使 ,再延长BA到D,使 ,则线段CD的长为( )A、10cm B、8cm C、6cm D、12cm9. 下列各式运算正确的是( )A、2(a﹣1)=2a﹣1 B、a2b﹣ab2=0 C、a2+a2=2a2 D、2a3﹣3a3=a310. 已知关于x的一元一次方程 的解是整数,则符合条件的所有整数a的和为( )A、 B、 C、2 D、611. 如图∠AOB=60°,射线OC平分∠AOB , 以OC为一边作∠COP=15°,则∠BOP=( )
4. 若 , , ,则 , , , 这四个数的大小关系是( )A、 B、 C、 D、5. 一种商品,降价10%后的售价是 元,则原价为( )A、 元 B、 元 C、 元 D、 元6. 下列采用的调查方式中,不合适的是( )A、了解永安溪的水质,采用抽样调查 B、检测神舟十二号飞船的零部件质量,采用抽样调查 C、了解我县中学生视力情况,采用抽样调查 D、了解某班同学的数学成绩,采用全面调查7. 按规律排列的一组数据: , ,□, , , ,…,其中□内应填的数是( )A、 B、 C、 D、8. 线段AB的长为2cm,延长AB到C,使 ,再延长BA到D,使 ,则线段CD的长为( )A、10cm B、8cm C、6cm D、12cm9. 下列各式运算正确的是( )A、2(a﹣1)=2a﹣1 B、a2b﹣ab2=0 C、a2+a2=2a2 D、2a3﹣3a3=a310. 已知关于x的一元一次方程 的解是整数,则符合条件的所有整数a的和为( )A、 B、 C、2 D、611. 如图∠AOB=60°,射线OC平分∠AOB , 以OC为一边作∠COP=15°,则∠BOP=( )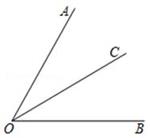 A、15° B、45° C、15°或30° D、15°或45°12. 某服装店销售某新款羽绒服,标价为300元,若按标价的八折销售,仍可款利60元.设这款服装的进价为x元,根据题意可列方程为( )A、300-0.2x=60 B、300-0.8x=60 C、300×0.2-x=60 D、300×0.8-x=60
A、15° B、45° C、15°或30° D、15°或45°12. 某服装店销售某新款羽绒服,标价为300元,若按标价的八折销售,仍可款利60元.设这款服装的进价为x元,根据题意可列方程为( )A、300-0.2x=60 B、300-0.8x=60 C、300×0.2-x=60 D、300×0.8-x=60二、填空题
-
13. 如果单项式 与单项式 是同类项,则 的值为.14. 把一条长为20厘米的线段分成三段,如果中间一段长为8厘米,那么第一段中点到第三段中点间的距离等于厘米.15. 单位换算: ″.16. 如图,直线 、 相交于点O, 平分 ,若 ,则
 17. 一家商店将某种服装按照成本价提高35%后标价,又以8折优惠卖出,结果每件服装仍获利25元,求这种服装每件的成本是多少元?设这种服装每件的成本是 元,则根据题意可列方程为.18. 中华文化源远流长,文学方面:《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生在寒假期间对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下两幅不完整的统计图:
17. 一家商店将某种服装按照成本价提高35%后标价,又以8折优惠卖出,结果每件服装仍获利25元,求这种服装每件的成本是多少元?设这种服装每件的成本是 元,则根据题意可列方程为.18. 中华文化源远流长,文学方面:《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生在寒假期间对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下两幅不完整的统计图: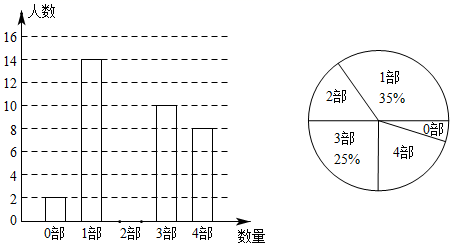
根据以上信息,本次调查所得数据中,扇形统计图中“读完了4部”所在扇形的圆心角为度;
三、解答题
-
19. 计算:(1)、(﹣ )×(﹣8)+(﹣6)2;(2)、﹣14+ .20. 解方程:(1)、2x﹣3(x﹣2)=4;(2)、 .21. 先化简,再求值: ,其中 , .22. 先化简,再求值:2x2y﹣[5xy2+2(x2y﹣3xy2+1)],其中x=2,y=-1.23. 如图所示, : : :5:3,OM平分 , ,求 和 .
 24. 市实验中学学生步行到郊外旅游.七(1)班学生组成前队,步行速度为4千米/时,七(2)班学生组成后队,速度为 6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.(1)、后队追上前队需要多长时间?(2)、后队追上前队时间内,联络员走的路程是多少?(3)、两队何时相距2千米?25. 如图所示,点C在线段AB上,点M、N分别是AC、BC的中点.
24. 市实验中学学生步行到郊外旅游.七(1)班学生组成前队,步行速度为4千米/时,七(2)班学生组成后队,速度为 6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.(1)、后队追上前队需要多长时间?(2)、后队追上前队时间内,联络员走的路程是多少?(3)、两队何时相距2千米?25. 如图所示,点C在线段AB上,点M、N分别是AC、BC的中点. (1)、若AC=8cm,CB=6cm,求线段MN的长.(2)、若C为线段AB上任意一点,满足AC+CB=a cm,其他条件不变,你能猜想出MN的长度吗?并说明理由.(3)、若C在线段AB的延长线上,且满足AC﹣CB=b cm,M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.
(1)、若AC=8cm,CB=6cm,求线段MN的长.(2)、若C为线段AB上任意一点,满足AC+CB=a cm,其他条件不变,你能猜想出MN的长度吗?并说明理由.(3)、若C在线段AB的延长线上,且满足AC﹣CB=b cm,M、N分别为AC、BC的中点,你能猜想出MN的长度吗?请画出图形,写出你的结论,并说明理由.