北师版数学九年级上册同步训练《1.3 正方形的性质与判定》
试卷更新日期:2021-08-24 类型:同步测试
一、单选题
-
1. 下列说法正确的是( )A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形2. 已知四边形 是平行四边形, , 相交于点O,下列结论错误的是( )A、 , B、当 时,四边形 是菱形 C、当 时,四边形 是矩形 D、当 且 时,四边形 是正方形3. 如图,在 中, , 和 关于直线BC对称,连接AD , 与BC相交于点O , 过点C作 ,垂足为C , 与AD相交于点E . 若 , ,则 的值为( )
 A、 B、 C、 D、4. 如图,在平行四边形ABCD中,对角线 , , , 为 的中点,E为边 上一点,直线 交 于点F,连结 , .下列结论不成立的是( )
A、 B、 C、 D、4. 如图,在平行四边形ABCD中,对角线 , , , 为 的中点,E为边 上一点,直线 交 于点F,连结 , .下列结论不成立的是( ) A、四边形 为平行四边形 B、若 ,则四边形 为矩形 C、若 ,则四边形 为菱形 D、若 ,则四边形 为正方形5. 如图,在正方形ABCD中,E为AB中点,连结DE,过点D作 交BC的延长线于点F,连结 若 ,则EF的值为
A、四边形 为平行四边形 B、若 ,则四边形 为矩形 C、若 ,则四边形 为菱形 D、若 ,则四边形 为正方形5. 如图,在正方形ABCD中,E为AB中点,连结DE,过点D作 交BC的延长线于点F,连结 若 ,则EF的值为 A、3 B、 C、 D、46. 如图,点E在正方形 的边 上,将 绕点A顺时针旋转 到 的位置,连接 ,过点A作 的垂线,垂足为点H,与 交于点G.若 , ,则 的长为( )
A、3 B、 C、 D、46. 如图,点E在正方形 的边 上,将 绕点A顺时针旋转 到 的位置,连接 ,过点A作 的垂线,垂足为点H,与 交于点G.若 , ,则 的长为( )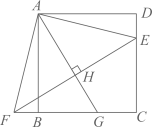 A、 B、 C、4 D、7. 如图,正方形 的边长为4,点E在 上且 ,F为对角线 上一动点,则 周长的最小值为( ).
A、 B、 C、4 D、7. 如图,正方形 的边长为4,点E在 上且 ,F为对角线 上一动点,则 周长的最小值为( ).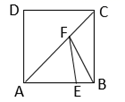 A、5 B、6 C、7 D、88. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )
A、5 B、6 C、7 D、88. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变,如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC′D′,若∠D′AB=30°,则菱形ABC′D′的面积与正方形ABCD的面积之比是( )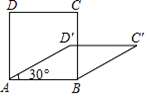 A、1 B、 C、 D、9. 如图,正方形ABCD的边长为3,E为BC边上一点,BE=1.将正方形沿GF折叠,使点A恰好与点E重合,连接AF , EF , GE , 则四边形AGEF的面积为( )
A、1 B、 C、 D、9. 如图,正方形ABCD的边长为3,E为BC边上一点,BE=1.将正方形沿GF折叠,使点A恰好与点E重合,连接AF , EF , GE , 则四边形AGEF的面积为( )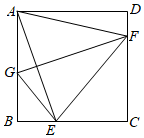 A、2 B、2 C、6 D、510. 如图,将正方形 放在平面直角坐标系中,O是坐标原点,点 ,则点F的坐标为( )
A、2 B、2 C、6 D、510. 如图,将正方形 放在平面直角坐标系中,O是坐标原点,点 ,则点F的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
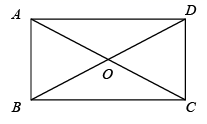
11. 如图,在矩形 中,对角线 相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使矩形 是正方形.
 12. 如图1,已知四边形ABCD是正方形,将 , 分别沿DE , DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点),若GF=4,EG=6,则DG的长为 .
12. 如图1,已知四边形ABCD是正方形,将 , 分别沿DE , DF向内折叠得到图2,此时DA与DC重合(A、C都落在G点),若GF=4,EG=6,则DG的长为 . 13. 如图,已知正方形 的边长为 ,点E是边 的中点,点P是对角线 上的动点,则 的最小值是.
13. 如图,已知正方形 的边长为 ,点E是边 的中点,点P是对角线 上的动点,则 的最小值是.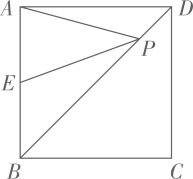 14. 如图,在边长为6的正方形 内作 , 交 于点 , 交 于点F,连接 ,将 绕点A顺时针旋转 得到 ,若 ,则 的长为.
14. 如图,在边长为6的正方形 内作 , 交 于点 , 交 于点F,连接 ,将 绕点A顺时针旋转 得到 ,若 ,则 的长为. 15. 如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为 则正方形ABCD的面积为
15. 如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为 则正方形ABCD的面积为 16. 如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE , EF , AF . 若 , ,则 的度数为 .
16. 如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE , EF , AF . 若 , ,则 的度数为 .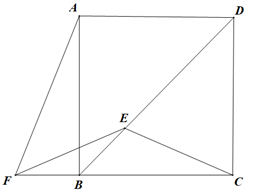
三、解答题
-
17. 如图,点E是正方形ABCD的边BC上的动点, ,且 , .
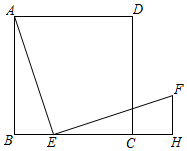 (1)、求证: ;(2)、若 , ,用x表示DF的长.18. 如图,正方形 ,G是 边上任意一点(不与B、C重合), 于点E, ,且交 于点F.
(1)、求证: ;(2)、若 , ,用x表示DF的长.18. 如图,正方形 ,G是 边上任意一点(不与B、C重合), 于点E, ,且交 于点F.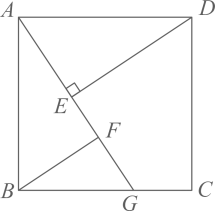 (1)、求证: ;(2)、四边形 是否可能是平行四边形,如果可能请指出此时点G的位置,如不可能请说明理由.19. 如图,在正方形 的外侧,作等边角形 ,连接 、 .
(1)、求证: ;(2)、四边形 是否可能是平行四边形,如果可能请指出此时点G的位置,如不可能请说明理由.19. 如图,在正方形 的外侧,作等边角形 ,连接 、 .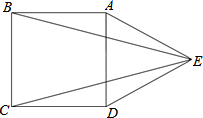 (1)、求证: ;(2)、求 的度数.20. 如图,点M, 分别在正方形 的边 , 上,且 ,把 绕点A顺时针旋转 得到 .
(1)、求证: ;(2)、求 的度数.20. 如图,点M, 分别在正方形 的边 , 上,且 ,把 绕点A顺时针旋转 得到 .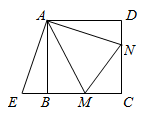 (1)、求证: ≌ .(2)、若 , ,求正方形 的边长.21. 如图,点 , 分别在正方形 的边 , 上,且 ,点 在射线 上(点 不与点 重合).将线段 绕点 顺时针旋转 得到线段 ,过点 作 的垂线 ,垂足为点 ,交射线 于点 .
(1)、求证: ≌ .(2)、若 , ,求正方形 的边长.21. 如图,点 , 分别在正方形 的边 , 上,且 ,点 在射线 上(点 不与点 重合).将线段 绕点 顺时针旋转 得到线段 ,过点 作 的垂线 ,垂足为点 ,交射线 于点 .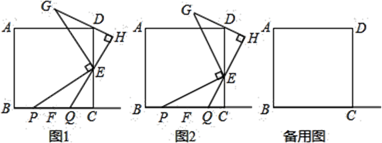 (1)、如图1,若点 是 的中点,点 在线段 上,线段 , , 的数量关系为.(2)、如图2,若点 不是 的中点,点 在线段 上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.(3)、正方形 的边长为6, , ,请直接写出线段 的长.22. 如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)、如图1,若点 是 的中点,点 在线段 上,线段 , , 的数量关系为.(2)、如图2,若点 不是 的中点,点 在线段 上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.(3)、正方形 的边长为6, , ,请直接写出线段 的长.22. 如图1,对角线互相垂直的四边形叫做垂美四边形.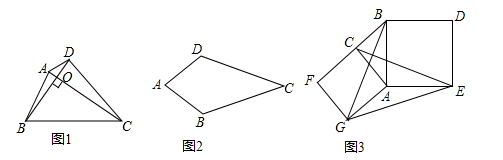 (1)、概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由;(2)、性质探究:如图1,四边形 的对角线 、 交于点 , .试证明: ;(3)、解决问题:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连结 、 、 .已知 , ,求 的长.
(1)、概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由;(2)、性质探究:如图1,四边形 的对角线 、 交于点 , .试证明: ;(3)、解决问题:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连结 、 、 .已知 , ,求 的长.