北师版数学九年级上册同步训练《1.2 矩形的性质与判定》
试卷更新日期:2021-08-24 类型:同步测试
一、单选题
-
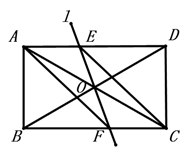
1. 如图, 为一长条形纸带, ,将 沿 折叠, 、 两点分别与 、 对应,若 ,则 的度数为( )
 A、60° B、65° C、72° D、75°2. 如图,将直角三角板放置在矩形纸片上,若 ,则 的度数为( )
A、60° B、65° C、72° D、75°2. 如图,将直角三角板放置在矩形纸片上,若 ,则 的度数为( ) A、42° B、48° C、52° D、60°3. 如图,将矩形纸片 沿 折叠后,点D、C分别落在点 、 的位置, 的延长线交 于点G,若 ,则 等于( )
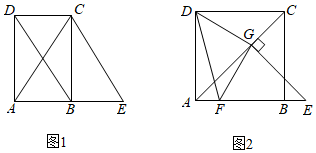
A、42° B、48° C、52° D、60°3. 如图,将矩形纸片 沿 折叠后,点D、C分别落在点 、 的位置, 的延长线交 于点G,若 ,则 等于( )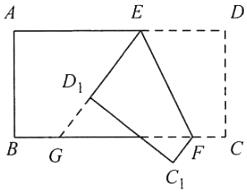 A、 B、 C、 D、4. 对角线互相垂直平分但不相等的四边形是( )A、正方形 B、菱形 C、矩形 D、平行四边形5. 如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )
A、 B、 C、 D、4. 对角线互相垂直平分但不相等的四边形是( )A、正方形 B、菱形 C、矩形 D、平行四边形5. 如图,在四边形ABCD中,∠A=∠C=90°,DF∥BC,∠ABC的平分线BE交DF于点G,GH⊥DF,点E恰好为DH的中点,若AE=3,CD=2,则GH=( )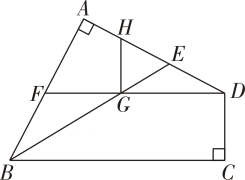 A、1 B、2 C、3 D、46. 将三角尺按如图所示放置在一张矩形纸片上,∠EGF=90°,∠FEG=30°,∠1=125°,则∠BFG的大小为( )
A、1 B、2 C、3 D、46. 将三角尺按如图所示放置在一张矩形纸片上,∠EGF=90°,∠FEG=30°,∠1=125°,则∠BFG的大小为( )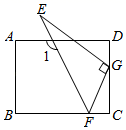 A、125° B、115° C、110° D、120°7. 如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )A、互相平分 B、相等 C、互相垂直 D、互相垂直平分8. 在矩形 中, 、 相交于点O,若 的面积为2,则矩形 的面积为( )
A、125° B、115° C、110° D、120°7. 如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )A、互相平分 B、相等 C、互相垂直 D、互相垂直平分8. 在矩形 中, 、 相交于点O,若 的面积为2,则矩形 的面积为( ) A、4 B、6 C、8 D、109. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( )
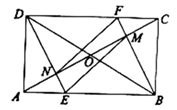
A、4 B、6 C、8 D、109. 如图,矩形 的对角线 , 交于点 , , ,过点 作 ,交 于点 ,过点 作 ,垂足为 ,则 的值为( ) A、 B、 C、 D、10. 如图,矩形 中, 相交于点O , 过点B作 交 于点F , 交 于点M , 过点D作 交 于点E , 交 于点N , 连接 .则下列结论:
A、 B、 C、 D、10. 如图,矩形 中, 相交于点O , 过点B作 交 于点F , 交 于点M , 过点D作 交 于点E , 交 于点N , 连接 .则下列结论:① ;② ;③ ;④当 时,四边形 是菱形.其中,正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图所示,线段 为等腰 的底边,矩形 的对角线 与 交于点 ,若 ,则 .
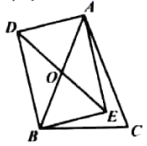 12. 如图,在矩形 中, ,点 和点 分别为 上的点,将 沿 翻折,使点 落在 上的点 处,过点 作 交 于点 ,过点 作 交 于点 .若四边形 与四边形 的面积相等,则 的长为.
12. 如图,在矩形 中, ,点 和点 分别为 上的点,将 沿 翻折,使点 落在 上的点 处,过点 作 交 于点 ,过点 作 交 于点 .若四边形 与四边形 的面积相等,则 的长为. 13. 如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 .
13. 如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 . 14. 如图,在边长为 的正方形 中,点 分别是边 的中点,连接 点 分别是 的中点,连接 ,则 的长度为.
14. 如图,在边长为 的正方形 中,点 分别是边 的中点,连接 点 分别是 的中点,连接 ,则 的长度为. 15. 在矩形 中, 2cm,将矩形 沿某直线折叠,使点B与点D重合,折痕与直线 交于点E,且 3cm,则矩形 的面积为cm2 .16. 如图,在矩形ABCD中, , ,若点M、N分别是线段DB、AB上的两个动点,则 的最小值为 .
15. 在矩形 中, 2cm,将矩形 沿某直线折叠,使点B与点D重合,折痕与直线 交于点E,且 3cm,则矩形 的面积为cm2 .16. 如图,在矩形ABCD中, , ,若点M、N分别是线段DB、AB上的两个动点,则 的最小值为 .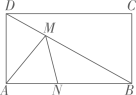
三、解答题
-
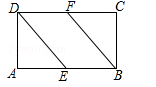
17. 如图,在矩形ABCD中,E,F分别是AB,CD的中点.求证:DE=BF.
 18. 如图,在矩形 ABCD中,点 E,F 在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
18. 如图,在矩形 ABCD中,点 E,F 在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明. 19. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF.
19. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=CD,连接CF. (1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.20. 如图,在矩形 中,点 在 上, ,且 ,垂足为 .
(1)、求证:△AEF≌△DEB;(2)、若AB=AC,试判断四边形ADCF的形状,并证明你的结论.20. 如图,在矩形 中,点 在 上, ,且 ,垂足为 . (1)、求证: ;(2)、若 ,求四边形 的面积.
(1)、求证: ;(2)、若 ,求四边形 的面积.