2022年苏科版初中数学《中考一轮复习》专题一 数与式 1.2 整式
试卷更新日期:2021-08-24 类型:一轮复习
一、单选题
-
1. 用式子表示“比a的2倍大1的数”是( ).A、 B、 C、 D、2. 下列结论中正确的是( )A、单项式 的系数是 ,次数是4 B、单项式m的次数是1,没有系数 C、多项式 是二次多项式 D、在 , , , ,0中,整式有4个3. 下列运算正确的是( )A、 B、 C、 D、4. 若 是关于 的一元二次方程 的一个根,则 的值为( )A、 B、 C、 D、5. 已知:(2021﹣a)(2020﹣a)=4,则(2021﹣a)2+(2020﹣a)2的值为( )A、7 B、8 C、9 D、126. 已知 ,则 的值为( )A、4 B、2 C、-2 D、-47. 今年金鸡百花奖有 部作品参赛,比上届参赛作品增加了 还多2部,上届参赛作品有( )A、 B、 C、 D、8. 记 ,则 ( )A、一个偶数 B、一个质数 C、一个整数的平方 D、一个整数的立方9. 如图1的8张宽为a,长为 的小长方形纸片,按如图2的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
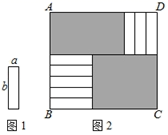 A、 B、 C、 D、10. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是
A、 B、 C、 D、10. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 为非负整数)的展开式中,把各项系数按一定的规律排成右表(展开后每一项按 的次数由大到小的顺序排列).人们把这个表叫做“杨辉三角”.据此规律,则 展开式中含 项的系数是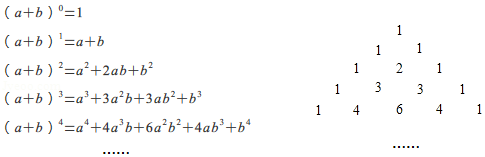 A、2016 B、2017 C、2018 D、2019
A、2016 B、2017 C、2018 D、2019二、填空题
-
11. 如果单项式 与单项式 是同类项,则 的值为.12. 计算: .13. 若 ,则 可表示为(用含a、b的代数式表示).14. 若 , ,则 .15. 已知 ,则 .16. 已知: , ,则 的值是;17. 若a=2018x+2019,b=2018x+2020,c=2018x+ 2021,则多项式a2+b2+c2-ab-ac-bc的值为18. 已知数 的大小关系如图所示:则下列各式:① ;② ;③ ;④ ;⑤ .其中正确的有(请填写编号).
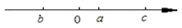
三、计算题
-
19. 计算:(1)、(2)、20. 先化简,再求值: ,其中 , .21. 先化简,再求值: ,其中
四、解答题
-
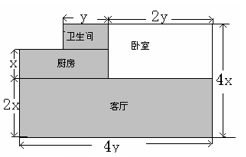
22. 某同学做一道数学题:“两多项式 、 , ,试求 ”,这位同学把“ ”看成“ ”,结果求出答案是 ,那么 的正确答案是多少?23. 已知:A=by2-ay-1,B=2y2+3ay-10y-1,且多项式2A-B的值与字母y的取值无关,求(2a2b+2ab2)-[2(a2b-1)+3ab2+2]的值。24. 一家住房的结构如下图所示,房子的主人打算把卧室以外的部分都铺上地板砖,至少需要多少平方米的地板砖?如果这种地板砖的价格为a元/平方米,那么购买地板砖至少需要多少元?
 25. 如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有 个点,每个图形的总点数记为S .
25. 如图所示,由一些点组成形如三角形的图形,每条“边”(包括两个顶点)有 个点,每个图形的总点数记为S . (1)、当 时,S的值为;当 时,S的值为;(2)、每条“边”有n个点时的总点数S是(用含n的式子表示);(3)、当 时,总点数S是多少?26. 若 满足 ,求 的值.
(1)、当 时,S的值为;当 时,S的值为;(2)、每条“边”有n个点时的总点数S是(用含n的式子表示);(3)、当 时,总点数S是多少?26. 若 满足 ,求 的值.解:设 , ,
则 , ,
∴ .
请仿照上面的方法求解下面问题:
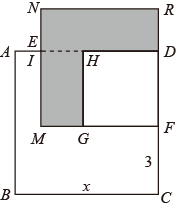 (1)、若 满足 ,求 的值;(2)、已知正方形 的边长为 , , 分别是 , 上的点,且 , ,长方形 的面积是35,分别以 , 为边作正方形 和正方形 ,求阴影部分的面积.27. 已知:(x-1)(x+1)=x2-1
(1)、若 满足 ,求 的值;(2)、已知正方形 的边长为 , , 分别是 , 上的点,且 , ,长方形 的面积是35,分别以 , 为边作正方形 和正方形 ,求阴影部分的面积.27. 已知:(x-1)(x+1)=x2-1(x-1)(x2+x+1)=x3-1
(x-1)(x3+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1
(1)、当x=3时,(3-1)×(33+32+3+1)=;……
(2)、试求:25+24+23+22+2+1的值.(3)、判断22021+22020+22019+……+22+2+1的值的个位数是;28.(1)、(知识生成)用两种不同方法计算同一图形的面积,可以得到一个等式,如图1,是用长为a,宽为b(a>b)的四个全等长方形拼成一个大正方形,用两种不同的方法计算阴影部分(小正方形)的面积,可以得到(a﹣b)2、(a+b)2、ab三者之间的等量关系式:; (2)、(知识迁移)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式,如图2,观察大正方体分割,可以得到等式:;(3)、已知x+y=6,xy= ,求x﹣y的值;(4)、已知|a+b﹣6|+(ab﹣7)2=0,求a3+b3的值.
(2)、(知识迁移)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式,如图2,观察大正方体分割,可以得到等式:;(3)、已知x+y=6,xy= ,求x﹣y的值;(4)、已知|a+b﹣6|+(ab﹣7)2=0,求a3+b3的值.