2022年苏科版初中数学《中考一轮复习》专题一 数与式 1.1 实数
试卷更新日期:2021-08-24 类型:一轮复习
一、单选题
-
1. 我国治霾任务仍然艰巨,根据国务院发布的《大气污染防治行动计划》,大气污染防治行动计划共需投入17500亿元,数据17500用科学记数法表示为( )A、175×103 B、1.75×105 C、1.75×104 D、1.75×1062. 某粮店出售的三种品牌的面粉袋上分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差( )
A、0.8kg B、0.6kg C、0.5kg D、0.4kg3. 在实数:﹣(﹣3.14159),1.010010001…,﹣(﹣1)2013 , , , , 中,分数有( )A、1个 B、2个 C、3个 D、4个4. 若=-a,则实数a在数轴上的对应点一定在 ( )A、原点左侧 B、原点右侧 C、原点或原点左侧 D、原点或原点右侧5. 有下列说法:①带根号的数是无理数;②不带根号的数一定是有理数;③负数没有立方根;④- 是17的平方根。其中正确的有( )A、0个 B、1个 C、2个 D、3个6. 对于实数、 , 给出以下三个判断:
①若 , 则 。
②若 , 则 。
③若 , 则 。其中正确的判断的个数是( )
A、3 B、2 C、1 D、07. 如图,在数轴上表示 的点在哪两个字母之间( ) A、B 与 C B、A 与 B C、A 与 C D、C 与 D8. 如图,下列结论正确的是( )
A、B 与 C B、A 与 B C、A 与 C D、C 与 D8. 如图,下列结论正确的是( )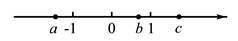 A、
A、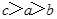 B、
B、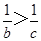 C、
C、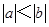 D、
D、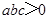 9. 若6- 的整数部分为x,小数部分为y,则(2x+ )y的值是( )A、5-3 B、3 C、3 -5 D、-310. 若x为实数,记{x}=x-[x](其中[x]表示不超过x的最大整数),则方程:2006x+{x}=的实根的个数是( ).
9. 若6- 的整数部分为x,小数部分为y,则(2x+ )y的值是( )A、5-3 B、3 C、3 -5 D、-310. 若x为实数,记{x}=x-[x](其中[x]表示不超过x的最大整数),则方程:2006x+{x}=的实根的个数是( ).
A、O B、1 C、2 D、大于2的整数二、填空题
-
11. 的平方根是 , 的相反数是 , .
12. 比较大小: ﹣3 .13. 若m>0,n<0,且|m|>|n|,用“<”把m,-m,n,-n连接起来 . (利用数轴解答)
14. 若 是一个正整数,满足条件的最小正整数n= .
15. 已知x2-x-1=0,则代数式-x3+2x2+2 018的值为 .16. 若x∶y∶z=2∶3∶4,且x+y+z=18,则xyz= .17. 已知a+ =5,则a2+ 的结果是 .18. 观察下列各式:; ;
计算:3×(1×2+2×3+3×4+…+99×100+100×101)= .
三、计算题
-
19. 计算:( +π)0﹣2|1﹣sin30°|+( )﹣1 .20. 计算:( )﹣1+( ﹣1)0+2sin45°+| ﹣2|.21. 计算.(1)、
(2)、四、解答题
-
22. 已知a,b,c在数轴上对应点的位置如图所示,化简|a|-|a+b|+ +|b-c|.
 23. 已知 .(1)、求a的值;(2)、求a2﹣b2的平方根.24. 定义新运算:对于任意实数 ,都有 ,等式右边是通常的加法、减法及乘法运算,比如:(1)、求 的值;(2)、若 的值小于13,求x的取值范围.25. 如图是一种数值转换的运算程序
23. 已知 .(1)、求a的值;(2)、求a2﹣b2的平方根.24. 定义新运算:对于任意实数 ,都有 ,等式右边是通常的加法、减法及乘法运算,比如:(1)、求 的值;(2)、若 的值小于13,求x的取值范围.25. 如图是一种数值转换的运算程序 (1)、若第1次输入的数为x=7,则第5次输出的数为;若第2次输出的数为7,则第1次输入的数为 .(2)、若第n次输出的数为32,求第(n+100)次输出的数是多少?(3)、是否存在输入的数x,使第2次输出的数是x的2倍?若存在,求出x的值;若不存在,请说明理由.26. 阅读材料,求值:1+2+22+23+24+…+22015 .
(1)、若第1次输入的数为x=7,则第5次输出的数为;若第2次输出的数为7,则第1次输入的数为 .(2)、若第n次输出的数为32,求第(n+100)次输出的数是多少?(3)、是否存在输入的数x,使第2次输出的数是x的2倍?若存在,求出x的值;若不存在,请说明理由.26. 阅读材料,求值:1+2+22+23+24+…+22015 .解:设S=1+2+22+23+24+…+22015 , 将等式两边同时乘以2得:
2S=2+22+23+24+…+22015+22016
将下式减去上式得2S﹣S=22016﹣1
即S=1+2+22+23+24+…+22015=22016﹣1
请你仿照此法计算:
(1)、1+2+22+23+…+210(2)、1+3+32+33+34+…+3n(其中n为正整数)27. 如图1,数轴上,O点与C点对应的数分别是0、60(单位:单位长度),将一根质地均匀的直尺AB放在数轴上(A在B的左边),若将直尺在数轴上水平移动,当A点移动到B点的位置时,B点与C点重合,当B点移动到A点的位置时,A点与O点重合. (1)、直尺的长为个单位长度(直接写答案)(2)、如图2,直尺AB在数轴上移动,有BC=3OA,求此时A点对应的数;
(1)、直尺的长为个单位长度(直接写答案)(2)、如图2,直尺AB在数轴上移动,有BC=3OA,求此时A点对应的数;
(3)、如图3,以OC为边搭一个横截面为长方形的不透明的篷子,将直尺放入篷内的数轴上的某处(看不到直尺的任何部分,A在B的左边),将直尺AB沿数轴以5个单位/秒的速度分别向左、向右移动,直到完全看到直尺,所经历的时间为t1、t2 , 若t1﹣t2=2(秒),求直尺放入蓬内,A点对应的数为多少?28. 如图,数轴上有A.B两点,AB=12,原点O是线段AB上的一点,OA=2OB. (1)、写出A,B两点所表示的实数;(2)、若点C是线段AB上一点,且满足AC=CO+CB,求C点所表示的实数;(3)、若动点P、Q分别从A.B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P、Q两点停止运动.
(1)、写出A,B两点所表示的实数;(2)、若点C是线段AB上一点,且满足AC=CO+CB,求C点所表示的实数;(3)、若动点P、Q分别从A.B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当点P与点Q重合时,P、Q两点停止运动.①当t为何值时,2OP﹣OQ=4;
②当点P到达点O时,动点M从点O出发,以每秒3个单位长的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动,求在此过程中,点M行驶的总路程和点M最后位置在数轴上对应的实数.