2021-2022学年人教版数学八年级上册名校期末测评卷

试卷更新日期：2021-08-24 类型：期末考试

进入出卷网下载

一、单选题

1. 1.在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列图形不具有稳定性的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，运算结果正确的是（）

A、 ${(x^{2})}^{3} = x^{5}$ B、 $x^{2} \cdot x^{3} = x^{5}$ C、 $x^{2} + x^{3} = x^{5}$ D、 $x^{10} \div x^{2} = x^{5}$

查看试题解析
4. 下列长度的线段中，与长度为3，5的两条线段能组成三角形的是（）

A、2 B、7 C、9 D、11

查看试题解析
5. 如图， $D E$ 是 $△ A B C$ 中 $A C$ 边的垂直平分线，若 $B C = 8$ 厘米， $A B = 10$ 厘米，则 $△ E B C$ 的周长为（）

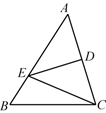A、16 B、18 C、26 D、28

查看试题解析
6. 如图，足球图片正中的黑色正五边形的外角和是（）

A、 $180^{\circ}$ B、 $360^{\circ}$ C、 $540^{\circ}$ D、 $720^{\circ}$

查看试题解析
7. 把多项式 $x^{2} - 3 x + 2$ 分解因式，下列结果正确的是（）

A、 $(x - 1) (x + 2)$ B、 $(x - 1) (x - 2)$ C、 $(x + 1) (x + 2)$ D、 $(x + 1) (x - 2)$

查看试题解析
8. 已知关于 $x$ 的分式方程 $\frac{m - 2}{x + 1} = 1$ 的解是非正数，则m的取值范围是（）

A、 $m \leq 3$ B、 $m \leq 3$ 且 $m \neq 2$ C、 $m < 3$ D、 $m < 3$ 且 $m \neq 2$

查看试题解析
9. 如图，D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，若AB=5，CF=3，则BD的长是（）

A、2 B、1.5 C、1 D、0.5

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ ， $C E$ 是 $△ A B C$ 的两条中线， $P$ 是 $A D$ 上个动点，则下列线段的长度等于 $B P + E P$ 最小值的是（）

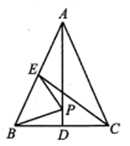A、BC B、CE C、AD D、AC

查看试题解析

二、填空题

11. 已知a+b=7，ab=-8，则a²+b²= ．

查看试题解析
12. 若等腰三角形中有两边长分别为2和5，则这个三角形的周长为 .

查看试题解析
13. 若分式 $\frac{|x| - 2}{x^{2} - 5 x + 6}$ 的值为零，则x的值是．

查看试题解析
14. 已知等腰三角形的两边长分别为x和y，且x和y满足|x﹣5|+（y﹣2）²=0，则这个等腰三角形的周长为．

查看试题解析
15. 如图，一种滑翔伞的形状是左右成轴对称的四边形ABCD，其中∠BAD=150°，∠B=40°，则∠ACD的度数是°.

查看试题解析
16. 若关于x的分式方程 $\frac{x}{x - 1} + 2 = \frac{m}{1 - x}$ 有增根，则m的值为.

查看试题解析
17. 如图，已知∠ABC=∠DCB添加下列条件中的一个：

① ∠A=∠D，②AC=DB，③AB=DC，其中不能确定△ABC≌△DCB的是(只填序号)

查看试题解析
18. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O ，过点O作EF∥BC交AB于E ，交AC于F ，过点O作OD⊥AC于D ，下列四个结论：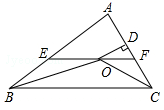

①EF=BE+CF；

②∠BOC=90°+ $\frac{1}{2}$ ∠A；

③点O到△ABC各边的距离相等；

④设OD=m ， AE+AF=n ，则 $S_{Δ A E F} = m n$ ．

其中正确的结论是．（填序号）

查看试题解析

三、计算题

19. 因式分解：

(1)、 $25 x^{2} - 16 y^{2}$ ；

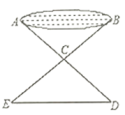
(2)、 $a^{2} b - 4 a b^{2} + 4 b^{3}$

查看试题解析
20. 解分式方程：

(1)、 $\frac{2}{x} = \frac{5}{x + 3}$

(2)、 $\frac{x}{x - 1} - \frac{2 x - 1}{x^{2} - 1} = 1$

查看试题解析
21. 先化简，再求值： $(2 - a) (3 + a) + {(a - 5)}^{2}$ ，其中 $a = 4$ .

查看试题解析
22. 如图，有一个池塘，要测池塘两端 $A$ ， $B$ 的距离，可先在平地上取一个点 $C$ ，从点 $C$ 不经过池塘可以直接达到点 $A$ 和 $B$ ，连接 $A C$ 并延长到点 $D$ ，使 $C D = C A$ ，连接 $B C$ 并延长到点 $E$ ，使 $C E = C B$ ，连接 $D E$ ，那么量出 $D E$ 的长度就是 $A$ ， $B$ 的距离，为什么？

查看试题解析
23. △ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上．

⑴作出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；

⑵作出△ABC关于y对称的△A₂B₂C₂ ，并写出点C₂的坐标．

⑶求△ABC的面积．

查看试题解析
24. 先化简 $(\frac{3}{x - 1} - x - 1) \div \frac{x - 2}{x^{2} - 2 x + 1}$ ，再选一个你喜欢的x值代入求值.

查看试题解析
25. 节能又环保的油电混合动力汽车，既可以用油做动力行驶，也可以用电做动力行驶，某品牌油电混合动力汽车从甲地行驶到乙地，若完全用油做动力行驶，则费用为80元；若完全用电做动力行驶，则费用为30元，已知汽车行驶中每千米用油费用比用电费用多0.5元.

(1)、求：汽车行驶中每千米用电费用是多少元？甲、乙两地的距离是多少千米？

(2)、若汽车从甲地到乙地采用油电混合动力行驶，且所需费用不超过50元，则至少需要用电行驶多少千米？

查看试题解析
26. 在平面直角坐标系中，已知 $A (- 3 ， 0)$ ， $B (0 ， 3)$ ，点 $C$ 为 $x$ 轴正半轴上一动点，过点 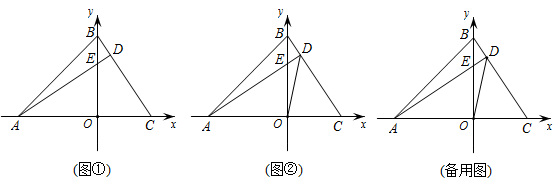$A$ 作 $A D ⊥ B C$ 交 $y$ 轴于点 $E$ .

(1)、如图①，若点C的坐标为 $(2 ， 0)$ ，试求点E的坐标；

(2)、如图②，若点C在x正半轴上运动，且 $O C < 3$ ，其它条件不变，连接 $O D$ ，求证： $O D$ 平分 $∠ A D C$ ；

(3)、若点C在x轴正半轴上运动，当 $A D - C D = O C$ 时，求 $∠ O C D$ 的度数.

查看试题解析
27.

(1)、如图（1），在△ABC中，AB=AC，∠BAC=90°，过点A作AH⊥BC于H，求证： $A H = \frac{1}{2} B C$ .

(2)、如图（2），在△ABC 和△ADE中，AB=AC，AD=AE，且∠BAC＝∠DAE＝90°，∠ABC＝∠ADE＝45°，点D、B、C在同一条直线上，AH为△ABC中BC边上的高，连接CE.则∠DCE的度数为，同时猜想线段AH、CD、CE之间的数量关系，并说明理由.

(3)、在如图（3）的两张图中，在△ABC中，AB=AC，且∠BAC=90°，在同一平面内有一点P，满足PC=l，PB=6，且∠BPC= 90°，请直接写出点A到BP的距离.

查看试题解析