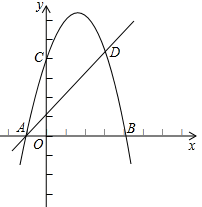浙江省嵊州市三界片2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-08-24 类型:期中考试
一、单选题
-
1. 二次函数y =(x-1)2 - 2的顶点坐标是( )A、(- 1,- 2) B、(- 1,2) C、(1,- 2) D、(1,2)2. 将抛物线 的图象先向右平移4个单位,再向下平移3个单位所得的解析式为( )A、 B、 C、 D、3. 下列事件中,是必然事件的为( )A、3天内会下雨 B、打开电视,正在播放广告 C、367人中至少有2人公历生日相同 D、某妇产医院里,下一个出生的婴儿是女孩4. 在圆内接四边形ABCD中,∠A:∠B:∠C:∠D的度数之比可能是( )A、1:2:3:4 B、4:2:1:3 C、4:2:3:1 D、1:3:2:45.
如图,△ABC内接于⊙O,∠A=40°,则∠BOC的度数为( )
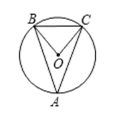 A、20° B、40° C、60° D、80°6. 如图, 是圆 的直径, 于 , , ,则 为( )
A、20° B、40° C、60° D、80°6. 如图, 是圆 的直径, 于 , , ,则 为( )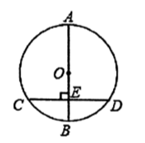 A、2 B、3 C、4 D、3.57.
A、2 B、3 C、4 D、3.57.如图,当半径为30cm的转动轮转过120°角时,传送带上的物体A平移的距离为( )
 A、900лcm B、300лcm C、60лcm D、20лc m8. 已知点C、D是以AB为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( )
A、900лcm B、300лcm C、60лcm D、20лc m8. 已知点C、D是以AB为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( )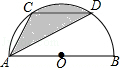 A、 B、 C、 D、9. 如图,二次函数 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是( )
A、 B、 C、 D、9. 如图,二次函数 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是( )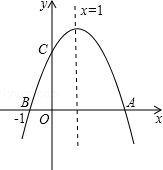 A、1 B、2 C、3 D、410. 若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )A、 ≤m<1 B、 <m≤1 C、1<m≤2 D、1<m<2
A、1 B、2 C、3 D、410. 若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )A、 ≤m<1 B、 <m≤1 C、1<m≤2 D、1<m<2二、填空题
-
11. 十字路口的交通信号灯每分钟红灯亮30秒,绿灯亮25秒,黄灯亮5秒,当你抬头看信号时,是黄灯的概率是.12. 已知 是二次函数,则m= .13. 某公司对一批某一品牌的衬衣的质量抽检结果如下表:
抽查件数
50
100
200
300
400
500
次品件数
0
4
16
19
24
30
则从这批衬衣中任抽1件是次品的概率约为.
14. 如图,点A , B , C在圆O上,∠ACB=54°,则∠ABO的度数是.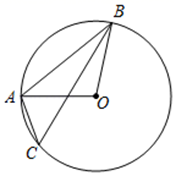 15. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为度.
15. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为度.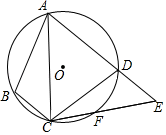 16. 已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是.
16. 已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是.三、解答题
-
17. 已知二次函数(1)、求函数图象的对称轴;(2)、求函数图象的顶点坐标.18. 甲、乙玩转盘游戏时,把质地相同的两个转盘A、B平均分成2份和3份,并在每一份内标有数 字如图.游戏规则:甲、乙两人分别同时转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数 时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.
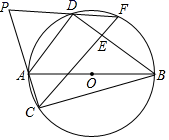
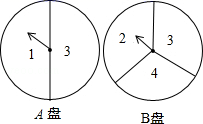 (1)、用画树状图或列表的方法,求甲获胜的概率;(2)、这个游戏对甲、乙双方公平吗?请判断并说明理由.19. 如图, 、 、 、 是 上的四点, .求证: .
(1)、用画树状图或列表的方法,求甲获胜的概率;(2)、这个游戏对甲、乙双方公平吗?请判断并说明理由.19. 如图, 、 、 、 是 上的四点, .求证: . 20. 如图,已知二次函数 的图象经过 , 两点.
20. 如图,已知二次函数 的图象经过 , 两点. (1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.21. 已知:如图,△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC 于点D,∠BAE与∠CAD相等吗?若相等,请给出证明;若不相等, 请说明理由
(1)、求这个二次函数的解析式;(2)、设该二次函数的对称轴与 轴交于点 ,连接 , ,求 的面积.21. 已知:如图,△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC 于点D,∠BAE与∠CAD相等吗?若相等,请给出证明;若不相等, 请说明理由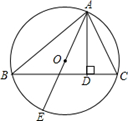 22. 某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)、求出每天所得的销售利润w(单位:元)与每件涨价x(单位:元)之间的函数关系式;(2)、求销售单价为多少元时,该商品每天的销售利润最大;(3)、商场的营销部在调控价格方面,提出了A,B两种营销方案.
22. 某商品的进价为每件20元,售价为每件25元时,每天可卖出250件.市场调查反映:如果调整价格,一件商品每涨价1元,每天要少卖出10件.(1)、求出每天所得的销售利润w(单位:元)与每件涨价x(单位:元)之间的函数关系式;(2)、求销售单价为多少元时,该商品每天的销售利润最大;(3)、商场的营销部在调控价格方面,提出了A,B两种营销方案.方案A:每件商品涨价不超过5元;
方案B:每件商品的利润至少为16元.
请比较哪种方案的最大利润更高,并说明理由.