浙江省绍兴市越城区2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-08-24 类型:期中考试
一、单选题
-
1. 对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=-1 C、顶点坐标是(1,2) D、与x轴有两个交点2. 如图所示圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,已知点A与点B的距离是2cm,若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出的圆的直径是( )
 A、1cm B、2cm C、4cm D、3. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、154. 对于函数y=﹣x2﹣2x﹣2,使得y随x的增大而增大的x的取值范围是( )A、x≥﹣1 B、x≥0 C、x≤0 D、x≤﹣15. 将抛物线 通过平移得到 ,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 对于二次函数y=ax2+bx+c(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点,则二次函数y=x2﹣mx﹣5(m为实数)的零点的个数是( )A、1 B、2 C、0 D、不能确定7. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
A、1cm B、2cm C、4cm D、3. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、154. 对于函数y=﹣x2﹣2x﹣2,使得y随x的增大而增大的x的取值范围是( )A、x≥﹣1 B、x≥0 C、x≤0 D、x≤﹣15. 将抛物线 通过平移得到 ,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 对于二次函数y=ax2+bx+c(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点,则二次函数y=x2﹣mx﹣5(m为实数)的零点的个数是( )A、1 B、2 C、0 D、不能确定7. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )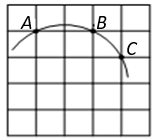 A、(0,0) B、(-1,1) C、(-1,0) D、(-1,-1)8. 某建筑物,从10m高的窗口A , 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( )
A、(0,0) B、(-1,1) C、(-1,0) D、(-1,-1)8. 某建筑物,从10m高的窗口A , 用水管向外喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),如图所示,如果抛物线的最高点M离墙1m,离地面 m,则水流落地点B离墙的距离OB是( ) A、2m B、3m C、4m D、5m9. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.
A、2m B、3m C、4m D、5m9. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是( )
 A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-2)x+c的图象可能是( )
A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b-2)x+c的图象可能是( )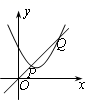 A、
A、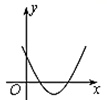 B、
B、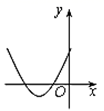 C、
C、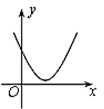 D、
D、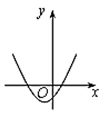
二、填空题
-
11. 已知 ,则 =.12. 从甲地到乙地有A,B,C三条不同的公交线路.为了解决早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时
公交车用时的频数
线路
合计
A
59
151
166
124
500
B
50
50
122
278
500
C
45
265
167
23
500
早高峰期间,乘坐(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
13. 如图,A,B,C,D为⊙O上的点,OC⊥AB于点E.若∠CDB=30°,OA=2,则AB的长为.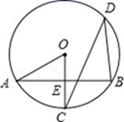 14. 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,则选取点B为坐标原点时的抛物线解析式是 .
14. 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,则选取点B为坐标原点时的抛物线解析式是 . 15. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm , 则球的半径为cm.
15. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4cm , 则球的半径为cm.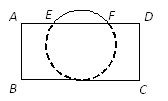 16. 如图,直线l: 经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这种抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时美丽抛物线相应的d的值是.
16. 如图,直线l: 经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这种抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时美丽抛物线相应的d的值是.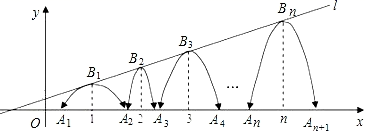
三、解答题
-
17. 已知抛物线的解析式为y=﹣3x2+6x+9.(1)、求它的对称轴;(2)、求它与x轴,y轴的交点坐标.18. 某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m, 分别用 、 、 表示 ;田赛项目:跳远,跳高 分别用 、 表示 .(1)、该同学从5个项目中任选一个,恰好是田赛项目的概率为;(2)、该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.19. 如图,已知二次函数 的图象过A(2,0),B(0,-1)和C(4,5)三点.
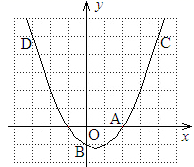 (1)、求二次函数的解析式;(2)、设二次函数的图象与
(1)、求二次函数的解析式;(2)、设二次函数的图象与 轴的另一个交点为D,求点D的坐标; (3)、在同一坐标系中画出直线 ,并写出当
轴的另一个交点为D,求点D的坐标; (3)、在同一坐标系中画出直线 ,并写出当 在什么范围内时,一次函数的值大于二次函数的值. 20. 如图,已知点A、B的坐标分别是(0,0) ,(4,0),将 绕A点按逆时针方向旋转90°后得到 .
在什么范围内时,一次函数的值大于二次函数的值. 20. 如图,已知点A、B的坐标分别是(0,0) ,(4,0),将 绕A点按逆时针方向旋转90°后得到 . (1)、画出 (不要求写出作法);(2)、写出点 的坐标;(3)、求旋转过程中点B所经过的路径长.21. 某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型.已知这座桥的跨度L=32米,拱高h=8米.
(1)、画出 (不要求写出作法);(2)、写出点 的坐标;(3)、求旋转过程中点B所经过的路径长.21. 某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型.已知这座桥的跨度L=32米,拱高h=8米.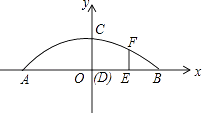 (1)、如果设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;(2)、如果设计成圆弧型,求该圆弧所在圆的半径;(3)、在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)、不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:
(1)、如果设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;(2)、如果设计成圆弧型,求该圆弧所在圆的半径;(3)、在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)、不妨设该种品牌玩具的销售单价为在40元的基础上上涨x(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润W(元),并把结果填写在表格中:销售单价(元)
40+x
销售量y(件)
销售玩具获得利润W(元)
(2)、在(1)问条件下,若商场获得10000元销售利润,则该玩具销售单价应定为多少元?(3)、在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?23. 我们知道:有一内角为直角的三角形叫做直角三角形.类似地,我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(﹣4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列),BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然△DCE、△DEF、△DAE是半直角三角形. (1)、求证:△ABC是半直角三角形;(2)、求证:∠DEC=∠DEA;(3)、若点D的坐标为(0,8),求AE的长.24. 如图,已知二次函数y=x2+bx+c的图象经过A , B两点,BC⊥x轴于点C , 且点A(﹣1,0),C(4,0),AC=BC.
(1)、求证:△ABC是半直角三角形;(2)、求证:∠DEC=∠DEA;(3)、若点D的坐标为(0,8),求AE的长.24. 如图,已知二次函数y=x2+bx+c的图象经过A , B两点,BC⊥x轴于点C , 且点A(﹣1,0),C(4,0),AC=BC.
 (1)、求抛物线的解析式;(2)、点E是线段AB上一动点(不与A , B重合),过点E作x轴的垂线,交抛物线于点F , 当线段EF的长度最大时,求点E的坐标及S△ABF;(3)、点P是抛物线对称轴上的一个动点,是否存在这样的P点,使△ABP成为直角三角形?若存在,直接写出所有点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点E是线段AB上一动点(不与A , B重合),过点E作x轴的垂线,交抛物线于点F , 当线段EF的长度最大时,求点E的坐标及S△ABF;(3)、点P是抛物线对称轴上的一个动点,是否存在这样的P点,使△ABP成为直角三角形?若存在,直接写出所有点P的坐标;若不存在,请说明理由.