广西壮族自治区百色市德保县2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-08-24 类型:期中考试
一、单选题
-
1. 下列函数是二次函数的是 ( )A、 B、 C、 D、2. 二次函数 的图象的顶点坐标是( )A、(1,3) B、(
 ,3)
C、(1,
,3)
C、(1,  )
D、(
)
D、(  ,
,  )
3. 若反比例函数y= 的图象经过点(2,-1),则该反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限4. 若 ,则 等于 ( )A、 B、 C、 D、5. 下列两个图形一定相似的是( )A、矩形 B、菱形 C、直角三角形 D、有一个内角为 的等腰三角形6. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )
)
3. 若反比例函数y= 的图象经过点(2,-1),则该反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限4. 若 ,则 等于 ( )A、 B、 C、 D、5. 下列两个图形一定相似的是( )A、矩形 B、菱形 C、直角三角形 D、有一个内角为 的等腰三角形6. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )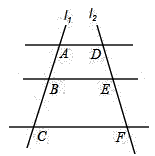 A、3.6 B、4.8 C、5 D、5,27. 已知点 (-2, ), (3, )是反比例函数 图象上的两点,则有( )A、 B、 C、 D、8. 在△ 中, ,用直尺和圆规在AC上确定点D,使△BAD∽△CBD,根据作图痕迹判断,正确的是( )A、
A、3.6 B、4.8 C、5 D、5,27. 已知点 (-2, ), (3, )是反比例函数 图象上的两点,则有( )A、 B、 C、 D、8. 在△ 中, ,用直尺和圆规在AC上确定点D,使△BAD∽△CBD,根据作图痕迹判断,正确的是( )A、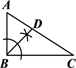 B、
B、 C、
C、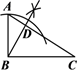 D、
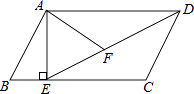
D、 9. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
9. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )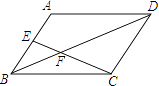 A、 B、 C、 D、10. 已知反比例函数 的图象如图所示,则二次函数 的图象大致为( ).
A、 B、 C、 D、10. 已知反比例函数 的图象如图所示,则二次函数 的图象大致为( ). A、
A、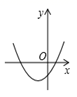 B、
B、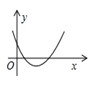 C、
C、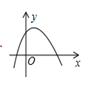 D、
D、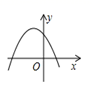 11. 如图,A、B是函数 的图象上关于原点对称的任意两点,BC∥ x轴,AC∥y轴, ABC的面积记为S,则( )
11. 如图,A、B是函数 的图象上关于原点对称的任意两点,BC∥ x轴,AC∥y轴, ABC的面积记为S,则( ) A、 B、 C、 D、12. 正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )A、
A、 B、 C、 D、12. 正方形ABCD边长为1,E,F,G,H分别为边AB,BC,CD,DA上的点,且AE=BF=CG=DH.设小正方形EFGH的面积为y,AE=x. 则y关于x的函数图象大致是( )A、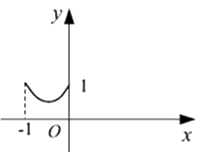 B、
B、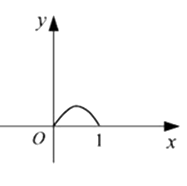 C、
C、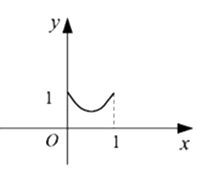 D、
D、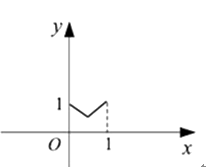
二、填空题
-
13. 已知: ( ),则 =.14. 如图是二次函数 图象的一部分,其对称轴为直线 ,若其与 轴一交点为 ,则由图象可知,方程 的解是.
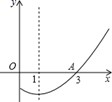 15. 在△ABC中,已知D、E分别为边AB、AC的中点,若△ADE的周长为3cm,则△ABC的周长为 cm.16. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m)
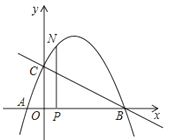
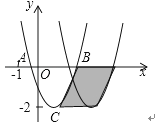
15. 在△ABC中,已知D、E分别为边AB、AC的中点,若△ADE的周长为3cm,则△ABC的周长为 cm.16. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m) 17. 某产品的进价为50元,该产品的日销量 (件)是日销价 (元)的反比例函数,且当售价为每件100元时,每日可售出40件,为获得日利润为1500元,售价应定为.18. 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论正确的是 .(写出所有正确结论的序号)
17. 某产品的进价为50元,该产品的日销量 (件)是日销价 (元)的反比例函数,且当售价为每件100元时,每日可售出40件,为获得日利润为1500元,售价应定为.18. 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1 , 则下列结论正确的是 .(写出所有正确结论的序号)①b>0
②a﹣b+c<0
③阴影部分的面积为4
④若c=﹣1,则b2=4a.
三、解答题
-
19. 如图,已知 是线段 上的点, 是 延长线上的点,且 , , ,求 的长.
 20. 已知:抛物线 与直线 交于点P(1,m).(1)、求m的值;(2)、求抛物线的解析式.21. 如图,已知 与 相交于点 , // , , , ,求 和 的长.
20. 已知:抛物线 与直线 交于点P(1,m).(1)、求m的值;(2)、求抛物线的解析式.21. 如图,已知 与 相交于点 , // , , , ,求 和 的长. 22. 已知二次函数 (m是常数)(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿x轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?23. 如图,从某建筑物9米高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面12米,建立平面直角坐标系,如图.
22. 已知二次函数 (m是常数)(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿x轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?23. 如图,从某建筑物9米高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面12米,建立平面直角坐标系,如图. (1)、求抛物线的解析式;(2)、求水流落地点B离墙的距离OB.24. 如图,已知反比例函数y1= 与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.
(1)、求抛物线的解析式;(2)、求水流落地点B离墙的距离OB.24. 如图,已知反比例函数y1= 与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.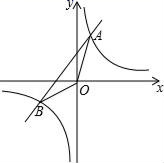 (1)、求k1 , k2 , b的值;(2)、求△AOB的面积;(3)、请直接写出不等式 ≤ x+b的解.
(1)、求k1 , k2 , b的值;(2)、求△AOB的面积;(3)、请直接写出不等式 ≤ x+b的解.