广西柳州市三江县2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-08-24 类型:期中考试
一、单选题
-
1. 下列生活安全警示标志图片,其中是中心对称图形的是( )A、
 有电危险
B、
有电危险
B、 当心触电安全
C、
当心触电安全
C、 当心滑落安全
D、
当心滑落安全
D、 注意安全
2. 下列方程属于一元二次方程的是( )A、 B、 C、 D、3. 把抛物线 向上移动3个单位得到抛物线表达式为( )A、 B、 C、 D、4. 根据抛物线y=x2+3x﹣1与x轴的交点坐标,可以求出下列方程中哪个方程的近似解( )
注意安全
2. 下列方程属于一元二次方程的是( )A、 B、 C、 D、3. 把抛物线 向上移动3个单位得到抛物线表达式为( )A、 B、 C、 D、4. 根据抛物线y=x2+3x﹣1与x轴的交点坐标,可以求出下列方程中哪个方程的近似解( )
A、x2﹣1=﹣3x B、x2+3x+1=0 C、3x2+x﹣1=0 D、x2﹣3x+1=05. 抛物线 的顶点坐标是( )A、 B、 C、 D、6. 一元二次方程 的根是( )A、 , B、 , C、 , D、7. 如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是 A、 B、 C、 D、8. 已知2x2+x﹣1=0的两根为x1、x2 , 则x1•x2的值为( )A、1 B、﹣1 C、 D、9. 关于x的二次函数y=x2﹣mx+5,当x≥1时,y随x的增大而增大,则实数m的取值范围是( )A、m<2 B、m=2 C、m≤2 D、m≥210. 如图,若 绕点 按逆时针方向旋转 后能与 重合,则 ( ).
A、 B、 C、 D、8. 已知2x2+x﹣1=0的两根为x1、x2 , 则x1•x2的值为( )A、1 B、﹣1 C、 D、9. 关于x的二次函数y=x2﹣mx+5,当x≥1时,y随x的增大而增大,则实数m的取值范围是( )A、m<2 B、m=2 C、m≤2 D、m≥210. 如图,若 绕点 按逆时针方向旋转 后能与 重合,则 ( ). A、 B、 C、 D、11. 用配方法解下列方程时,配方有错误的是( ).A、x2-2x-99=0化为(x-1)2=100 B、x2+8x+9=0化为(x+4)2=25 C、2t2-7t-4=0化为 D、3y2-4y-2=0化为12. 已知二次函数 的图象如图,有下列5个结论:① ;② ;③ ;④ ;⑤ ,其中正确的个数有( )
A、 B、 C、 D、11. 用配方法解下列方程时,配方有错误的是( ).A、x2-2x-99=0化为(x-1)2=100 B、x2+8x+9=0化为(x+4)2=25 C、2t2-7t-4=0化为 D、3y2-4y-2=0化为12. 已知二次函数 的图象如图,有下列5个结论:① ;② ;③ ;④ ;⑤ ,其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知抛物线 ,过点(0,2),则c=.14. 若 ,则 .15. 如果m是方程x2-2x-6=0的一个根,那么代数式2m-m2+7的值为 .16. 若关于 的方程 有两个不相等的实数根,则 的取值范围是 .17. 疫情期间,学校利用一段已有的围墙(可利用的围墙长度仅有5米)搭建一个矩形临时隔离点ABCD,如图所示,它的另外三边所围的总长度是10米,矩形隔离点的面积为12平方米,则AB的长度是米.
 18. 如图,抛物线 与x轴交于点O,A,把抛物线在x轴及其上方的部分记为 ,将 以y轴为对称轴作轴对称得到 , 与x轴交于点B,若直线y = m与 , 共有4个不同的交点,则m的取值范围是.
18. 如图,抛物线 与x轴交于点O,A,把抛物线在x轴及其上方的部分记为 ,将 以y轴为对称轴作轴对称得到 , 与x轴交于点B,若直线y = m与 , 共有4个不同的交点,则m的取值范围是.
三、解答题
-
19. 解方程:x2﹣3x=2(3﹣x).20. 抛物线的顶点为 ,且过点 ,求它的函数解析式.21. 如图, 在平面直角坐标系内,三个顶点的坐标分别为 , , .
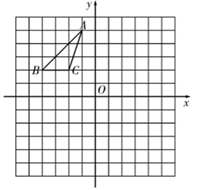
( 1 )平移 ,使点 移动到点 ,画出平移后的 ,并写出点 , 的坐标;
( 2 )画出 关于原点 对称的 ;
( 3 )线段 的长度为_▲_.
22. 现代互联网技术的广泛应用,催生了快递行业的高速发展.据调查,我市一家“大学生自主创业”的快递公司,今年7月份与9月份完成投递的快递总件数分别是10万件和12.1万件,现假设该公司每月投递的快递总件数的增长率相同.(1)、求该快递公司投递总件数的月平均增长率;(2)、如果每人每月最多可投递0.6万件,那么该公司现有的22名快递业务员能否完成今年10月份的快递投递任务?请说明理由.23. 已知抛物线 与 轴交于 两点,与 轴交于点 ,顶点为 .(1)、求抛物线的表达式及点D的坐标;(2)、判断 的形状.24. 某超市销售一款“免洗洗手液”,这款“免洗洗手液”的成本价为每瓶16元,当销售单价定为20元时,每天可售出80瓶.根据市场行情,现决定降价销售.市场调查反映:销售单价每降低0.5元,则每天可多售出20瓶(销售单价不低于成本价),若设这款“免洗洗手液”的销售单价为x(元),每天的销售量为y(瓶).(1)、求每天的销售量y(瓶)与销售单价x(元)之间的函数关系式;(2)、当销售单价为多少元时,销售这款“免洗洗手液”每天的销售利润最大,最大利润为多少元?25. 知识经验我们知道,如果两个因式的积为0,那么这两个因式中至少有一个等于0;反之,如果两个因式中任何一个为0,那么它们的积也等于0.
即:如果 ,那么 或
知识迁移
Ⅰ.解方程:
解: ,
或 ,
∴ 或 .
Ⅱ.解方程: ,
解: ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ ,
∴ 或 ,
∴ 或 .
(1)、【理解应用】
解方程:(2)、【拓展应用】
如图,有一块长宽分别为80 ,60 的矩形硬纸板,在它的四个角上分别剪去四个相同的小正方形,然后将四周突出的部分折起来,就可以做成底面积为1500 的无盖的长方体盒子,求所剪去的小正方形的边长. 26. 如图,在平面直角坐标系中,已知抛物线 与 轴交于 、 两点,与y轴交于点C,其顶点为点D,点E的坐标为 ,该抛物线与BE交于另一点F,连接BC.
26. 如图,在平面直角坐标系中,已知抛物线 与 轴交于 、 两点,与y轴交于点C,其顶点为点D,点E的坐标为 ,该抛物线与BE交于另一点F,连接BC. (1)、求该抛物线的解析式;(2)、若点 在BC上,连接FH,求 的面积;(3)、一动点M从点D出发,以每秒1个单位的速度沿平行于 轴方向向上运动,连接OM,BM,设运动时间为t秒 ,在点M的运动过程中,当t为何值时, ?
(1)、求该抛物线的解析式;(2)、若点 在BC上,连接FH,求 的面积;(3)、一动点M从点D出发,以每秒1个单位的速度沿平行于 轴方向向上运动,连接OM,BM,设运动时间为t秒 ,在点M的运动过程中,当t为何值时, ?