浙江省台州市三区三校2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2021-08-24 类型：期中考试
一、单选题
-
1. 已知三角形的两边长分别为3cm和9cm，则此三角形的第三边的长可能是（ ）A、4cm B、7cm C、6cm D、13cm2. △ABC中，∠A=20°，∠B=70°，则∠C=（ ）A、70° B、90° C、20° D、110°3. 若一个多边形的内角和是其外角和的4倍，则这个多边形的边数是（ ）A、7 B、8 C、9 D、104. 如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA等于（ ）
A、30° B、36° C、45° D、32°5. 两个等腰三角形，若顶角和底边对应相等，则两个等腰三角形全等，其理由是（ ）A、SAS B、SSS C、ASA D、ASA或AAS6. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（ ）
A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确7. 下列图形中：①平行四边形；②有一个角是30°的直角三角形；③长方形；④等腰三角形. 其中是轴对称图形有（ ）个A、1个 B、2个 C、3个 D、4个8. 已知点M（1﹣2m，1﹣m）关于x轴的对称点在第四象限，则m的取值范围在数轴上表示正确的是（ ）A、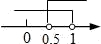
B、
C、
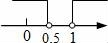D、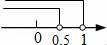
9. 如图，在 中，∠BAC=90°，AB=3，AC=4，将 沿直线BC方向平移2.5个单位得到 ，AC与DE相交于G点，连接AD，AE，则下列结论：① ；② 为等腰三角形；③AC平分∠EAD；④四边形AEFD的面积为9.其中正确的个数是（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，在 中，AB=20cm，AC=12cm，点P从点B出发以每秒3cm的速度向点A运动，点Q从点A同时出发以每秒2cm的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动，当AP=AQ时，点P、点Q运动的时间是（ ）
A、4秒 B、3.5秒 C、3秒 D、2.5秒二、填空题
-
11. 已知△ABC≌△DEF，∠A=50°，∠B=60°，则∠C=.12. 点A（-3，3）关于y轴的对称点 的坐标为.13. 一个三角形的三条高线的交点在三角形的外部，则这个三角形是 三角形14. 如果a，b，c为一个三角形的三边长，那么点 在第象限.15. 如图， 的高AD和它的角平分线BE相交于点F，若∠ABC=52°，∠C=44°，则 .
16. 如果一个三角形的两个内角α与β满足2α+β=90°，那么我们称这样的三角形为“准互余三角形”.若 是“准互余三角形”，∠C＞90°，∠A=20°，则∠B=.17. 如图，点P是 的角平分线OC上一点，PN OB于点N，点M是线段ON上一点，已知OM=3，ON=4，点D为OA上一点，若满足PD=PM，则OD的长度为
18. 如图，点P在AC上，点Q在AB上，BE平分∠ABP，交AC于E，CF平分∠ACQ，交AB于F，BE、CF相交于G，CQ、BP相交于D，若∠BDC=140°，∠BGC=110°，则∠A的度数为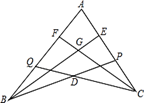
三、解答题
-
19. 折叠如图所示的直角三角形纸片ABC，使点C落在AB上的点E处，折痕为AD（点D在BC边上），用直尺和圆规画出折痕AD．（保留作图痕迹，不写作法）．
20. 已知：如图，D是AB上的一点，E是AC上一点，BE、CD相交于点F，∠A=62°，∠ACD=35°，∠ABE=20°.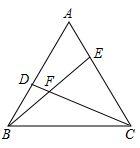
求：
(1)、∠BDC的度数；(2)、∠BFC的度数.21. 如图，∠B=42°，∠1=∠2+10°，∠ACD=64°，∠ACD的平分线与BA的延长线相交于点E.
(1)、请你判断BF与CD的位置关系，并说明理由；(2)、求∠3的度数.22. 如图，在△ABC中，线段BC的垂直平分线DE交AC于点D.
(1)、若AB=3，AC=8，求△ABD的周长；(2)、若△ABD的周长为13，△ABC的周长为20，求BC的长.23. 如图1，CA=CB，CD=CE，∠ACB=∠DCE=α.
(1)、求证：BE=AD；(2)、当α=90°时，取AD，BE的中点分别为点P、Q，连接CP，CQ，PQ，如图②，判断△CPQ的形状，并加以证明.
24. 如图
(1)、如图1，请证明∠A+∠B+∠C＝180°(2)、如图2的图形我们把它称为“8字形”，请证明∠A+∠B＝∠C+∠D(3)、如图3，E在DC的延长线上，AP平分∠BAD，CP平分∠BCE，猜想∠P与∠B、∠D之间的关系，并证明(4)、如图4，AB∥CD，PA平分∠BAC，PC平分∠ACD，过点P作PM、PE交CD于M，交AB于E，则①∠1+∠2+∠3+∠4不变；②∠3+∠4﹣∠1﹣∠2不变，选择正确的并给予证明.