浙江省嵊州市三界片2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2021-08-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若三角形的两条边长分别为6cm和10cm，则它的第三边长不可能为（）

A、5cm B、8cm C、10cm D、17cm

查看试题解析
3. 下列语句不是命题的是（）.

A、两直线平行，同位角相等 B、作直线 $A B$ 垂直于直线 $C D$ C、若 $| a | = | b |$ ，则 $a^{2} = b^{2}$ D、等角的补角相等

查看试题解析
4. 等腰三角形的两边分别为12和6，则这个三角形的周长是（）

A、24 B、18 C、30 D、24或30

查看试题解析
5. 式子：① $3 < 5$ ；② $4 x + 5 > 0$ ；③ $x = 3$ ；④ $x^{2} + x$ ；⑤ $x \neq - 4$ ；⑥ $x + 2 \geq x + 1$ .其中是不等式的有（）.

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 某实验室有一块三角形玻璃，被摔成如图所示的四块，胡老师想去店里买一块形状、大小与原来一样的玻璃，胡老师要带的玻璃编号是（）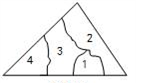

A、1 B、2 C、3 D、4

查看试题解析
7. 下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线，则对应选项中作法错误的是（）

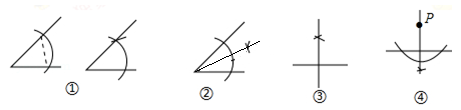A、① B、② C、③ D、④

查看试题解析
8. 直角三角形的两条直角边为3，4，则这个直角三角形斜边上的中线长为（）.

A、5 B、2.5 C、3.5 D、4.5

查看试题解析
9. 如图，折叠长方形纸片 $A B C D$ 的一边 $A D$ ，使点 $D$ 落在 $B C$ 边上的点 $F$ 处，已知 $A B = 8 c m$ ， $A D = 10 c m$ ，则折痕 $E F$ 的长为（）.

A、 $2 c m$ B、 $3 c m$ C、 $4 c m$ D、 $5 c m$

查看试题解析
10. 如图， $△ A B C$ 和 $△ A D E$ 都是等腰直角三角形， $∠ B A C = ∠ D A E = 90 °$ ，连结 $C E$ 交 $A D$ 于点 $F$ ，连结 $B D$ 交 $C E$ 于点 $G$ ，连结 $B E$ .下列结论中：

（1） $C E = B D$ ，（2） $△ A D C$ 是等腰直角三角形，（3） $∠ A D B = ∠ A E B$ ，（4） $S_{四边形 BCDE} = \frac{1}{2} B D \cdot C E$ ，（5） $B C^{2} + D E^{2} = B E^{2} + C D^{2}$ .
正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 在Rt△ABC中，∠C=90°，∠A=65°，则∠B=

查看试题解析
12. 命题“等腰三角形两底角相等”的逆命题是。

查看试题解析
13. 一副分别含有30°和45°的直角三角板，拼成如图，则 $∠ B F D$ 的度数是.

查看试题解析
14. 如图，等腰三角形 $Δ A B C$ 中， $A B = A C$ ， $A D$ 是底边上的高，若 $A B = 5 cm$ ， $B C = 6 cm$ ，则 $A D =$ $cm$ .

查看试题解析
15. 若一个直角三角形两边长为12和5，第三边长为.

查看试题解析
16. 如图，在△ABC中，∠C=90°，AD平分∠BAC，且CD=5，则点D到AB的距离为

查看试题解析
17. 如图，在 $△ ABC$ 中 $∠ A = 120 ° ， AB = AC ， BC = 6 cm ， AB$ 的垂直平分线交 $BC$ 于点 $M$ ，交 $AB$ 于点 $E$ ， $AC$ 的垂直平分线交 $BC$ 于点 $N$ ，交 $AC$ 于点 $F$ ，则 $MN$ 的长 $cm$ .

查看试题解析
18. 如图，已知 $∠ A B C = ∠ D C B$ ，则需添加的一个条件是可使 $△ A C B ≌ △ D B C$ .（只写一个即可，不添加辅助线）.

查看试题解析
19. 如图，在等边 $△ A B C$ 的 $A C$ ， $B C$ 边上各取一点 $P$ 、 $Q$ ，使 $A P = C Q$ ， $A Q$ ， $B P$ 相交于点 $O$ ，则 $∠ B O Q =$ 度.

查看试题解析
20. 如图，直线 $a ， b$ 相交于点 $O$ ， $∠ 1 ＝ 50 °$ ，点 $A$ 是直线上的一个定点，点 $B$ 在直线 $b$ 上运动，若以点 $O$ ， $A$ ， $B$ 为顶点的三角形是等腰三角形，则 $∠ O A B$ 的度数是.

查看试题解析

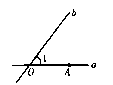
三、解答题

21. 解不等式（组）并把解表示在数轴上

(1)、 $3 x + 2 > 14$

(2)、 $\frac{1 + x}{2} - \frac{2 x + 1}{3} \leq 1$

查看试题解析
22. 已知，如图，点 $D$ ， $E$ 分别在 $A B$ ， $A C$ 上， $∠ B = ∠ C$ ， $A B = A C$ .

求证： $△ A E B ≌ △ A C D$ .

查看试题解析
23. 如图， $A B // C D$ ， $△ E F G$ 的顶点 $F$ ， $G$ 分别落在直线 $A B$ ， $C D$ 上， $G E$ 交 $A B$ 于点 $H$ ， $G E$ 平分 $∠ F G D$ .若 $∠ E F G = 90^{\circ}$ ， $∠ E = 35^{\circ}$ ，求 $∠ E F B$ 的度数.

查看试题解析
24. 如图，在△ABC 中，AB=AC，CD是∠ACB的平分线，DE∥BC，交AC于点 E.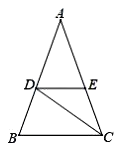

(1)、求证：DE=CE.

(2)、若∠CDE=25°，求∠A 的度数.

查看试题解析
25. 已知：如图， $B E ⊥ C D$ 于点 $E$ ， $B E = D E$ ， $B C = D A$ .

(1)、求证： $△ B C E ≌ △ D A E$

(2)、判断 $D F$ 与 $B C$ 的位置关系，并说明理由.

查看试题解析
26. 如图， $A B ⊥ B C$ ， $C D ⊥ B C$ ，且 $B C = C D = 4 c m$ ， $A B = 1 c m$ ，点 $P$ 以每秒 $0.5 c m$ 的速度从点 $B$ 开始沿射线 $B C$ 运动，同时点 $Q$ 在线段 $C D$ 上由点 $C$ 向终点 $D$ 运动.设运动时间为 $t$ 秒.

(1)、当 $t = 2$ 时， $B P =$ $c m$ ， $C P =$ $c m$ .

(2)、如图①，当点 $P$ 与点 $Q$ 经过几秒时，使得 $△ A B P$ 与 $△ P C Q$ 全等？此时，点 $Q$ 的速度是多少？（注：只求一种情况即可，并写出求解过程）

(3)、如图②，是否存在点 $P$ ，使得 $△ A D P$ 是等腰三角形？若存在，请直接写出 $t$ 的值，若不存在，请说明理由.

查看试题解析