浙江省杭州市萧山区城北片区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2021-08-24 类型:期中考试
一、单选题
-
1. 下面的图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知一个三角形的两条边长分别为4和6,则第三条边的长度不能是( )A、4 B、7 C、11 D、33. 如果关于x的不等式 的解集为 ,那么a的取值范围是( )A、 B、 C、 D、4. 一副三角板如图所示摆放,则 与 的数量关系为( )
2. 已知一个三角形的两条边长分别为4和6,则第三条边的长度不能是( )A、4 B、7 C、11 D、33. 如果关于x的不等式 的解集为 ,那么a的取值范围是( )A、 B、 C、 D、4. 一副三角板如图所示摆放,则 与 的数量关系为( )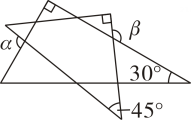 A、 B、 C、 D、5. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )
A、 B、 C、 D、5. 如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于( )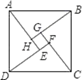 A、2 B、4 C、6 D、86. 如图是用直尺和圆规作角平分线的示意图,通过证明△DOP≌△EOP可以说明OC是∠AOB的角平分线,那么△DOP≌△EOP的依据是( )
A、2 B、4 C、6 D、86. 如图是用直尺和圆规作角平分线的示意图,通过证明△DOP≌△EOP可以说明OC是∠AOB的角平分线,那么△DOP≌△EOP的依据是( )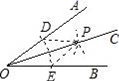 A、SSS B、SAS C、ASA D、AAS7. 已知直角三角形纸片的两条直角边长分别为m和3(m 3),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )A、m2+6m+9=0 B、m2﹣6m+9=0 C、m2+6m﹣9=0 D、m2﹣6m﹣9=08. 下列命题中,真命题有( )
A、SSS B、SAS C、ASA D、AAS7. 已知直角三角形纸片的两条直角边长分别为m和3(m 3),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )A、m2+6m+9=0 B、m2﹣6m+9=0 C、m2+6m﹣9=0 D、m2﹣6m﹣9=08. 下列命题中,真命题有( )①有一个角为60°的三角形是等边三角形;②底边相等的两个等腰三角形全等;③有一个角是40°,腰相等的两个等腰三角形全等;④一边上的中线等于这条边的一半的三角形是直角三角形.
A、1个 B、2个 C、3个 D、4个9. 如图,在△ABC中,AC=AB,∠BAC=90°,BD平分∠ABC,与AC相交于点F,CD⊥BD,垂足为D,交BA的延长线于点E,AH⊥BC交BD于点M,交BC于点H,下列选项不正确的是( )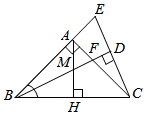 A、∠E=67.5° B、∠AMF=∠AFM C、BF=2CD D、BD=AB+AF10. 如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )
A、∠E=67.5° B、∠AMF=∠AFM C、BF=2CD D、BD=AB+AF10. 如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )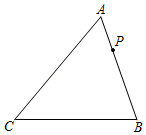 A、50° B、60° C、70° D、80°
A、50° B、60° C、70° D、80°二、填空题
-
11. 已知命题“全等三角形的面积相等.”写出它的逆命题: , 该逆命题是命题(填“真”或“假”).12. 疫情期间全国“停课不停学”初中生郑兴同学网上听课每节课a分钟,每天六节课,每天上网课总时长小于240分钟,可列不等式 .13. 等腰三角形的腰长为17,底长为16,则其底边上的高为.14. 如图,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=4,CE=3,则DE=.
 15. 如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为
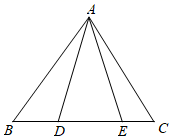
15. 如图,Rt△ABC,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为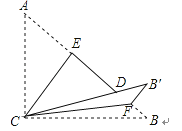 16. 如图,△ABC的面积是16,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是 .
16. 如图,△ABC的面积是16,点D,E,F,G分别是BC,AD,BE,CE的中点,则△AFG的面积是 .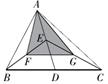
三、解答题
-
17.(1)、若x>y,比较﹣3x+5与﹣3y+5的大小,并说明理由;(2)、若x<y,且(a﹣3)x>(a﹣3)y,求a的取值范围.18. 如图
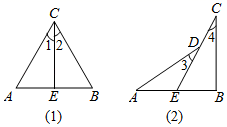 (1)、如图(1),已知CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌△BCE.(2)、如图(2),已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.19. 已知:如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°.
(1)、如图(1),已知CE与AB交于点E,AC=BC,∠1=∠2.求证:△ACE≌△BCE.(2)、如图(2),已知CD的延长线与AB交于点E,AD=BC,∠3=∠4.探究AE与BE的数量关系,并说明理由.19. 已知:如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°.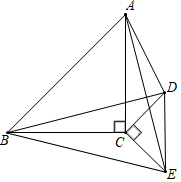 (1)、求证:BD=AE.(2)、若∠ABD=∠DAE,AB=8,AD=6,求四边形ABED的面积.20. 如图,已知等腰△ABC 中,AB=AC , ∠A<90°,CD 是△ABC 的高,BE 是△ABC 的角平分线,CD 与 BE 交于点 P . 当∠A 的大小变化时,△EPC 的形状也随之改变.
(1)、求证:BD=AE.(2)、若∠ABD=∠DAE,AB=8,AD=6,求四边形ABED的面积.20. 如图,已知等腰△ABC 中,AB=AC , ∠A<90°,CD 是△ABC 的高,BE 是△ABC 的角平分线,CD 与 BE 交于点 P . 当∠A 的大小变化时,△EPC 的形状也随之改变.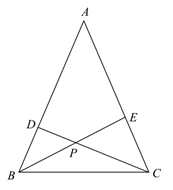 (1)、当∠A=44°时,求∠BPD 的度数;(2)、设∠A=x°,∠EPC=y°,求变量 y 与 x 的关系式;(3)、当△EPC 是等腰三角形时,请直接写出∠A 的度数.21. 如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,DE⊥BD,连结AC,CE.
(1)、当∠A=44°时,求∠BPD 的度数;(2)、设∠A=x°,∠EPC=y°,求变量 y 与 x 的关系式;(3)、当△EPC 是等腰三角形时,请直接写出∠A 的度数.21. 如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,DE⊥BD,连结AC,CE.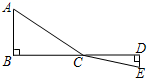 (1)、已知AB=3,DE=2,BD=12,设CD=x.用含x的代数式表示AC+CE的长;(2)、请问点C满足什么条件时,AC+CE的值最小?并求出它的最小值;(3)、根据(2)中的规律和结论,请构图求出代数式 的最小值.22. 如图, 是边上的两点,点P从点A开始沿 方向运动,且速度为每秒1cm,点Q从点B沿 运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)、已知AB=3,DE=2,BD=12,设CD=x.用含x的代数式表示AC+CE的长;(2)、请问点C满足什么条件时,AC+CE的值最小?并求出它的最小值;(3)、根据(2)中的规律和结论,请构图求出代数式 的最小值.22. 如图, 是边上的两点,点P从点A开始沿 方向运动,且速度为每秒1cm,点Q从点B沿 运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.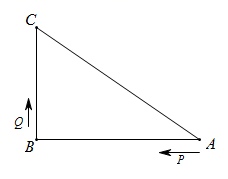 (1)、出发2秒后,求线段PQ的长;(2)、求点Q在BC上运动时,出发几秒后, 是等腰三角形;(3)、点Q在边CA上运动时,求能使 成为等腰三角形的运动时间.23. 在等腰三角形ABC中,(1)、若∠A=110°,则∠B=度;(2)、若∠A=40°,则∠B= ▲ 度.
(1)、出发2秒后,求线段PQ的长;(2)、求点Q在BC上运动时,出发几秒后, 是等腰三角形;(3)、点Q在边CA上运动时,求能使 成为等腰三角形的运动时间.23. 在等腰三角形ABC中,(1)、若∠A=110°,则∠B=度;(2)、若∠A=40°,则∠B= ▲ 度.通过上述解答,发现∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=α,求∠B的度数(用含α的式子表示).请你根据∠B的度数的个数探索α的取值范围.