广西壮族自治区南宁市宾阳县2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2021-08-24 类型：期中考试
一、单选题
-
1. 人字梯中间一般会设计一”拉杆”，这样做的道理是（ ）．
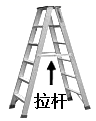A、两点之间，线段最短 B、垂线段最短 C、两直线平行，内错角相等 D、三角形具有稳定性2. 下列图形不是轴对称图形的是（ ）A、
B、
C、
D、
3. 下列说法中正确的是（ ）.A、三角形的三条高是三条直线 B、直角三角形只有一条高 C、锐角三角形的三条高都在三角形内 D、三角形每一边上的高都小于其他两边4. 已知点P（3，-2）与点Q关于y轴对称，则点Q的坐标为（ ）.A、（-3，-2） B、（-3，2） C、（3，2） D、（3，-2）5. 如果等腰三角形有一内角为50°，那么它的顶角的度数为（ ）.A、50° B、50°或80° C、50°或60° D、80°6. 如图，BE、CF都是△ABC的角平分线，且∠BDC=110°，则∠A=（ ）
A、50° B、40° C、70° D、35°7. 正多边形的一个外角的度数为30°，则这个正多边形的边数为（ ）.A、6 B、10 C、8 D、128. 如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为（ ）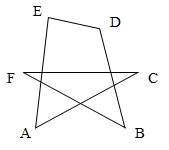
A、180° B、270° C、360° D、720°9. 使两个直角三角形全等的条件是A、一锐角对应相等 B、两锐角对应相等 C、一条边对应相等 D、两条边对应相等10. 如图，在△ABC中，∠C＝70º，沿图中虚线截去∠C，则∠1＋∠2＝（ ）
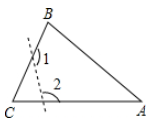A、360º B、250º C、180º D、140º11. 如图，是变压器中的L型硅钢片，其面积为（ ）
A、 B、 C、 D、12. 如图，边长为24的等边三角形ABC中，M是高CH所在直线上的一个动点，连结MB，将线段BM绕点B逆时针旋转60°得到BN，连结HN.则在点M运动过程中，线段HN长度的最小值是（ ）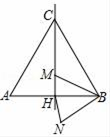
A、12 B、6 C、3 D、1二、填空题
-
13. 如图，已知△ABC≌△DEF，则DE=.
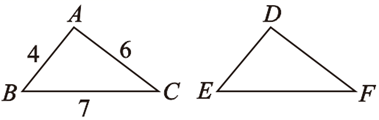14. 一个六边形共有条对角线.15. 若直角三角形的一锐角为30°，而斜边与较短边之和为24.那么斜边的长为.16. 如图，点D，E分别在线段AB，AC上，CD与BE相交于点P，已知AD＝AE．若△ABE≌△ACD，则可添加的条件为 ．
17. 如图，在△ABC中∠B= ，AB=BD，AD=CD，∠CAD的度数是
18. 如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为S△ABC ， S△ADF ， S△BEF ， 且S△ABC=18，则S△ADF－S△BEF=.
三、解答题
-
19. 已知：（x2+px+2）（x-1）的结果中不含x的二次项，求p2020的值.20. 如图，AE和BD相交于点C，∠A=∠E，AC=EC.求证：△ABC≌△EDC.
21. 先化简，再求值：[（3a﹣b）（a﹣2b）﹣b（a+2b）﹣a]÷2a，其中a＝ ，b＝﹣1.22. 如图，在平面直角坐标系xOy中，A(－1，5)，B(－1，0)，C(－4，3).
(1)、在图中作出△ABC关于y轴的对称图形△A1B1C1；(2)、写出点A1 ， B1 ， C1的坐标；(3)、求出△A1B1C1的面积.23. 已知，如图，∠C＝∠D＝90°，E是CD的中点，AE平分∠DAB.求证：BE平分∠ABC.
24. 上午8时，一条船从海岛A出发，以每小时航行18海里的速度向正北航行，10时到达海岛B处，从A，B望灯塔C，测得∠NAC=15°，∠NBC=30°.
(1)、求从海岛B到灯塔C的距离；(2)、在小灯塔C的周围20海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由.25. 如图，在 中， ， ，D是AB边上一点 点D与A，B不重合 ，连结CD，将线段CD绕点C按逆时针方向旋转 得到线段CE，连结DE交BC于点F，连接BE.
(1)、求证： ≌ ；26. 如图1，在边长为6的等边△ABC中，点D从点A开始在射线AB上运动，速度为1个单位/秒，点F同时从C出发，以相同的速度沿射线BC方向运动，过点D作DE⊥AC，连接DF交射线AC于点G，设点D的运动时间为t秒；
(1)、当DF⊥AB时，求t的值；(2)、当点D在线段AB上运动时，是否始终有DG=GF？若成立，请说明理由；(3)、小扬同学通过测量发现，当点D在线段AB上时，EG的长始终等于AC的一半，他想当点D运动到图2的情况时，EG的长是否发生变化？若改变，说明理由；若不变，求出EG的长.