四川省资阳市2021年中考数学试卷
试卷更新日期:2021-08-24 类型:中考真卷
一、选择题:(本大题共10个小题,每小题4分,共40分)
-
1. 下列计算正确的是( )A、a2+a2=2a4 B、a2⋅a=a3 C、(3a)2=6a2 D、a6+a2=a32. 如图是由6个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
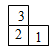 A、
A、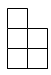 B、
B、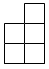 C、
C、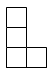 D、
D、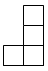 3. 如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( )
3. 如图,已知直线m∥n,∠1=40°,∠2=30°,则∠3的度数为( )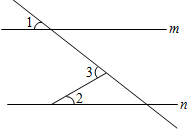 A、80° B、70° C、60° D、50°4. 15名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前8名,则他不仅要知道自己的成绩( )A、 平均数 B、众数 C、方差 D、中位数5. 若a= ,b= ,c=2,则a、b、c的大小关系为( )A、b<c<a B、b<a<c C、a<c<b D、a<b<c6. 下列命题正确的是( )A、每个内角都相等的多边形是正多边形 B、对角线互相平分的四边形是平行四边形 C、过线段中点的直线是线段的垂直平分线 D、三角形的中位线将三角形的面积分成1:2两部分7. 如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB= ,EF=1,则GM的长为( )
A、80° B、70° C、60° D、50°4. 15名学生演讲赛的成绩各不相同,若某选手想知道自己能否进入前8名,则他不仅要知道自己的成绩( )A、 平均数 B、众数 C、方差 D、中位数5. 若a= ,b= ,c=2,则a、b、c的大小关系为( )A、b<c<a B、b<a<c C、a<c<b D、a<b<c6. 下列命题正确的是( )A、每个内角都相等的多边形是正多边形 B、对角线互相平分的四边形是平行四边形 C、过线段中点的直线是线段的垂直平分线 D、三角形的中位线将三角形的面积分成1:2两部分7. 如图是中国古代数学家赵爽用来证明勾股定理的弦图的示意图,它是由四个全等的直角三角形和一个小正方形EFGH组成,恰好拼成一个大正方形ABCD.连结EG并延长交BC于点M.若AB= ,EF=1,则GM的长为( ) A、 B、 C、 D、8. 一对变量满足如图的函数关系.设计以下问题情境:
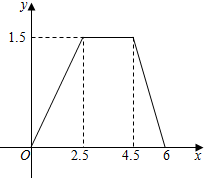
A、 B、 C、 D、8. 一对变量满足如图的函数关系.设计以下问题情境:①小明从家骑车以600米/分的速度匀速骑了2.5分钟,在原地停留了2分钟,然后以1000米/分的速度匀速骑回家.设所用时间为x分钟;②有一个容积为1.5升的开口空瓶,小张以0.6升/秒的速度匀速向这个空瓶注水,注满后停止,再以1升/秒的速度匀速倒空瓶中的水.设所用时间为x秒,瓶内水的体积为y升;③在矩形ABCD中,AB=2,BC=1.5,△ABP的面积为y.其中,符合图中函数关系的情境个数为( )
 A、3 B、2 C、1 D、09. 已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1 , y1)、Q(x2 , y2)两点.若x1<m≤x2 , 则a的取值范围为( )A、﹣4≤a<﹣ B、﹣4≤a≤﹣ C、﹣ ≤a<0 D、﹣ <a<0
A、3 B、2 C、1 D、09. 已知A、B两点的坐标分别为(3,﹣4)、(0,﹣2),线段AB上有一动点M(m,n),过点M作x轴的平行线交抛物线y=a(x﹣1)2+2于P(x1 , y1)、Q(x2 , y2)两点.若x1<m≤x2 , 则a的取值范围为( )A、﹣4≤a<﹣ B、﹣4≤a≤﹣ C、﹣ ≤a<0 D、﹣ <a<0二、填空题:(本大题共6个小题,每小题4分,共24分)
-
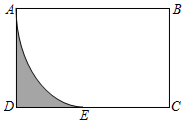
10. 中国共产党自1921年诞生以来,仅用了100年时间,党员人数从建党之初的50余名发展到如今约92000000名.11. 将2本艺术类、4本文学类、6本科技类的书籍混在一起.若小陈从中随机抽取一本,则抽中文学类的概率为 .12. 若x2+x﹣1=0,则3x﹣ =.13. 如图,在矩形ABCD中,AB=2cm,AD= cm以点B为圆心,AB长为半径画弧,交CD于点E,则图中阴影部分的面积为 cm2.
 14. 将一张圆形纸片(圆心为点O)沿直径MN对折后,按图1分成六等份折叠得到图2,再将△AOB展开得到如图3的一个六角星.若∠CDE=75°,则∠OBA的度数为 .
14. 将一张圆形纸片(圆心为点O)沿直径MN对折后,按图1分成六等份折叠得到图2,再将△AOB展开得到如图3的一个六角星.若∠CDE=75°,则∠OBA的度数为 . 15. 如图,在菱形ABCD中,∠BAD=120°,交CD于点G.FH⊥CD于点H,连结CF.有下列结论:①AF=CF2=EF•FG;③FG:EG=4:5;④cos∠GFH= .
15. 如图,在菱形ABCD中,∠BAD=120°,交CD于点G.FH⊥CD于点H,连结CF.有下列结论:①AF=CF2=EF•FG;③FG:EG=4:5;④cos∠GFH= .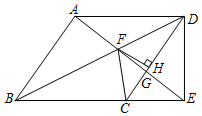
三、解答题:(本大题共8个小题,共86分)
-
16. 先化简,再求值:( ﹣ )÷ ,其中x﹣3=0.17. 目前,全国各地正在有序推进新冠疫苗接种工作.某单位为了解职工对疫苗接种的关注度,随机抽取了部分职工进行问卷调查(实时关注)、B(关注较多)、C(关注较少)(不关注)四类,现将调查结果绘制成如图所示的统计图.
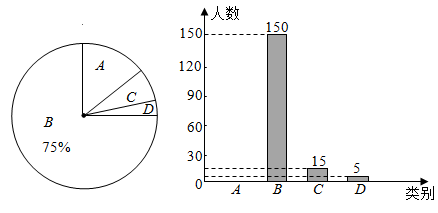
请根据图中信息,解答下列问题:
(1)、求C类职工所对应扇形的圆心角度数,并补全条形统计图;(2)、若D类职工中有3名女士和2名男士,现从中任意抽取2人进行随访,请用树状图或列表法求出恰好抽到一名女士和一名男士的概率.18. 我市某中学计划举行以“奋斗百年路,启航新征程”为主题的知识竞赛,并对获奖的同学给予奖励.现要购买甲、乙两种奖品,已知1件甲种奖品和2件乙种奖品共需40元,2件甲种奖品和3件乙种奖品共需70元.(1)、求甲、乙两种奖品的单价;(2)、根据颁奖计划,该中学需甲、乙两种奖品共60件,且甲种奖品的数量不少于乙种奖品数量的 , 应如何购买才能使总费用最少?并求出最少费用。19. 如图,已知直线y=kx+b(k≠0)与双曲线y= 相较于A(m,3)、B(3,n)两点. (1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.20. 如图,在△ABC中,AB=AC,DE⊥AC交BA的延长线于点E,交AC于点F.
(1)、求直线AB的解析式;(2)、连结AO并延长交双曲线于点C,连结BC交x轴于点D,连结AD,求△ABD的面积.20. 如图,在△ABC中,AB=AC,DE⊥AC交BA的延长线于点E,交AC于点F.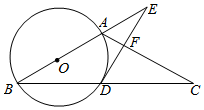 (1)、求证:DE是⊙O的切线;
(1)、求证:DE是⊙O的切线;
(2)、若AC=6,tanE= ,求AF的长.
21. 资阳市为实现5G网络全覆盖,2020﹣2025年拟建设5G基站七千个.如图,在坡度为i=1:2.4的斜坡CB上有一建成的基站塔AB,小芮在坡脚C测得塔顶A的仰角为45°,然后她沿坡面CB行走13米到达D处,在D处测得塔顶A的仰角为53°.(点A、B、C、D均在同一平面内)(参考数据:sin53°≈ ,cos53°≈ ,tan53°≈ ) (1)、求D处的竖直高度;
(1)、求D处的竖直高度;
(2)、求基站塔AB的高.
22. 已知,在△ABC中,∠BAC=90° (1)、如图1,已知点D在BC边上,∠DAE=90°,连结CE.试探究BD与CE的关系;(2)、如图2,已知点D在BC下方,∠DAE=90°,连结CE.若BD⊥AD,AB=2 ,AD交BC于点F,求AF的长;(3)、如图3,已知点D在BC下方,连结AD、BD、CD.若∠CBD=30°,AB2=6,AD2=4+ ,求sin∠BCD的值.23. 抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且B(﹣1,0),C(0,3).
(1)、如图1,已知点D在BC边上,∠DAE=90°,连结CE.试探究BD与CE的关系;(2)、如图2,已知点D在BC下方,∠DAE=90°,连结CE.若BD⊥AD,AB=2 ,AD交BC于点F,求AF的长;(3)、如图3,已知点D在BC下方,连结AD、BD、CD.若∠CBD=30°,AB2=6,AD2=4+ ,求sin∠BCD的值.23. 抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且B(﹣1,0),C(0,3). (1)、求抛物线的解析式;(2)、如图1,点P是抛物线上位于直线AC上方的一点,BP与AC相交于点E,求点P的坐标;
(1)、求抛物线的解析式;(2)、如图1,点P是抛物线上位于直线AC上方的一点,BP与AC相交于点E,求点P的坐标;
(3)、如图2,点D是抛物线的顶点,将抛物线沿CD方向平移,且DD'=2CD,点M是平移后所得抛物线上位于D'左侧的一点,连结CN.当 D'N+CN的值最小时