湖南省永州市2021年中考数学试卷
试卷更新日期:2021-08-24 类型:中考真卷
一、选择题(本大题共10个小题,每小题4分,共40分,)
-
1. -|-2021|的相反数为( )A、﹣2021 B、2021 C、﹣ D、2. 如图,在平面内将五角星绕其中心旋转180°后所得到的图案是( )
 A、
A、 B、
B、 C、
C、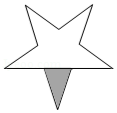 D、
D、 3. 据永州市2020年国民经济和社会发展统计公报,永州市全年全体居民人均可支配收入约为24000元,比上年增长6.5%,将“人均可支配收入”用科学记数法表示为( )A、24×103 B、2.4×104 C、2.4×105 D、0.24×1054. 已知一列数据:27,12,12,5,7,12,5.该列数据的众数是( )A、27 B、12 C、7 D、55. 下列计算正确的是( )A、(π﹣3)0=1 B、tan30°= C、 =±2 D、a2•a3=a66. 在一元一次不等式组 的解集中,整数解的个数是( )A、4 B、5 C、6 D、77. 如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若∠B=50°,则∠CAD的度数是( )
3. 据永州市2020年国民经济和社会发展统计公报,永州市全年全体居民人均可支配收入约为24000元,比上年增长6.5%,将“人均可支配收入”用科学记数法表示为( )A、24×103 B、2.4×104 C、2.4×105 D、0.24×1054. 已知一列数据:27,12,12,5,7,12,5.该列数据的众数是( )A、27 B、12 C、7 D、55. 下列计算正确的是( )A、(π﹣3)0=1 B、tan30°= C、 =±2 D、a2•a3=a66. 在一元一次不等式组 的解集中,整数解的个数是( )A、4 B、5 C、6 D、77. 如图,在△ABC中,AB=AC,分别以点A,B为圆心,大于 AB的长为半径画弧,两弧相交于点M和点N,作直线MN分别交BC、AB于点D和点E,若∠B=50°,则∠CAD的度数是( )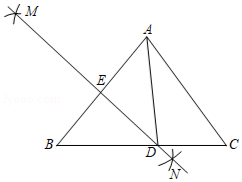 A、30° B、40° C、50° D、60°8. 中国传统数学重要著作《九章算术》中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?据此设计一类似问题:今有人组团购一物,如果每人出9元,则多了4元;如果每人出6元,则少了5元,问组团人数和物价各是多少?若设x人参与组团,物价为y元,则以下列出的方程组正确的是( )A、 B、 C、 D、9. 小明计划到永州市体验民俗文化,想从“零陵渔鼓、瑶族长鼓舞、东安武术、舜帝祭典”四种民俗文化中任意选择两项,则小明选择体验“瑶族长鼓舞、舜帝祭典”的概率为( )A、 B、 C、 D、10. 定义:若10x=N,则x=log10N,x称为以10为底的N的对数,简记为lgN,其满足运算法则:lgM+lgN=lg(M•N)(M>0,N>0).例如:因为102=100,所以2=lg100,亦即lg100=2;lg4+lg3=lg12.根据上述定义和运算法则,计算(lg2)2+lg2•lg5+lg5的结果为( )A、5 B、2 C、1 D、0
A、30° B、40° C、50° D、60°8. 中国传统数学重要著作《九章算术》中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?据此设计一类似问题:今有人组团购一物,如果每人出9元,则多了4元;如果每人出6元,则少了5元,问组团人数和物价各是多少?若设x人参与组团,物价为y元,则以下列出的方程组正确的是( )A、 B、 C、 D、9. 小明计划到永州市体验民俗文化,想从“零陵渔鼓、瑶族长鼓舞、东安武术、舜帝祭典”四种民俗文化中任意选择两项,则小明选择体验“瑶族长鼓舞、舜帝祭典”的概率为( )A、 B、 C、 D、10. 定义:若10x=N,则x=log10N,x称为以10为底的N的对数,简记为lgN,其满足运算法则:lgM+lgN=lg(M•N)(M>0,N>0).例如:因为102=100,所以2=lg100,亦即lg100=2;lg4+lg3=lg12.根据上述定义和运算法则,计算(lg2)2+lg2•lg5+lg5的结果为( )A、5 B、2 C、1 D、0二、填空题(本大题共8个小题,每小题4分,共32分,)
-
11. 在0, ,﹣0.101001,π, 中无理数的个数是 个.12. 已知二次根式 有意义,则x的取值范围是 .13. 请写出一个图象在第二、四象限的反比例函数的表达式:.14. 某初级中学坚持开展阳光体育活动,七年级至九年级每学期均进行体育技能测试.其中A班甲、乙两位同学6个学期的投篮技能测试成绩(投篮命中个数)折线图如图所示.为参加学校举行的毕业篮球友谊赛,A班需从甲、乙两位同学中选1人进入班球队,从两人成绩的稳定性考虑,请你决策A班应该选择的同学是 .
 15. 某同学在数学实践活动中,制作了一个侧面积为60π,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .
15. 某同学在数学实践活动中,制作了一个侧面积为60π,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .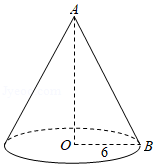 16. 如图,A,B两点的坐标分别为A(4,3),B(0,﹣3),在x轴上找一点P,使线段PA+PB的值最小,则点P的坐标是 .
16. 如图,A,B两点的坐标分别为A(4,3),B(0,﹣3),在x轴上找一点P,使线段PA+PB的值最小,则点P的坐标是 .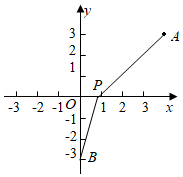 17. 已知函数y= ,若y=2,则x=.18. 若x,y均为实数,43x=2021,47y=2021,则:(1)、43xy•47xy=( )x+y;(2)、 =.
17. 已知函数y= ,若y=2,则x=.18. 若x,y均为实数,43x=2021,47y=2021,则:(1)、43xy•47xy=( )x+y;(2)、 =.三、解答题(共8小题,满分78分)
-
19. 先化简,再求值:(x+1)2+(2+x)(2﹣x),其中x=1.20. 若x1 , x2是关于x的一元二次方程ax2+bx+c=0的两个根,则x1+x2=﹣ ,x1•x2= .现已知一元二次方程px2+2x+q=0的两根分别为m,n.(1)、若m=2,n=﹣4,求p,q的值;(2)、若p=3,q=﹣1,求m+mn+n的值.21. 为庆祝中国共产党成立100周年,某校组织全校学生进行了一场党史知识竞赛活动根据竞赛结果,抽取了200名学生的成绩(得分均为正整数,满分为100分,大于80分的为优秀)进行统计,绘制了如图所示尚不完整的统计图表.
200名学生党史知识竞赛成绩的频数表
组别
频数
频率
A组(60.5~70.5)
a
0.3
B组(70.5~80.5)
30
0.15
C组(80.5~90.5)
50
b
D组(90.5~100.5)
60
0.3

请结合图表解决下列问题:
(1)、频数表中,a= , b=;(2)、请将频数分布直方图补充完整;(3)、抽取的200名学生中竞赛成绩的中位数落在的组别是 组;(4)、若该校共有1000名学生,请估计本次党史知识竞赛成绩为“优秀”的学生人数.22. 如图,已知点A,D,C,B在同一条直线上,AD=BC,AE=BF,AE∥BF.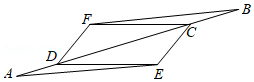 (1)、求证:△AEC≌△BFD.(2)、判断四边形DECF的形状,并证明.23. 永州市某村经济合作社在乡村振兴工作队的指导下,根据市场需求,计划在2022年将30亩土地全部用于种植A、B两种经济作物.预计B种经济作物亩产值比A种经济作物亩产值多2万元,为实现2022年A种经济作物年总产值20万元,B种经济作物年总产值30万元的目标,问:2022年A、B两种经济作物应各种植多少亩?24. 已知锐角△ABC中,角A、B、C的对边分别为a、b、c,边角总满足关系式: = = .
(1)、求证:△AEC≌△BFD.(2)、判断四边形DECF的形状,并证明.23. 永州市某村经济合作社在乡村振兴工作队的指导下,根据市场需求,计划在2022年将30亩土地全部用于种植A、B两种经济作物.预计B种经济作物亩产值比A种经济作物亩产值多2万元,为实现2022年A种经济作物年总产值20万元,B种经济作物年总产值30万元的目标,问:2022年A、B两种经济作物应各种植多少亩?24. 已知锐角△ABC中,角A、B、C的对边分别为a、b、c,边角总满足关系式: = = . (1)、如图1,若a=6,∠B=45°,∠C=75°,求b的值;(2)、某公园准备在园内一个锐角三角形水池ABC中建一座小型景观桥CD(如图2所示),若CD⊥AB,AC=14米,AB=10米,sin∠ACB= ,求景观桥CD的长度.25. 如图1,AB是⊙O的直径,点E是⊙O上一动点,且不与A,B两点重合,∠EAB的平分线交⊙O于点C,过点C作CD⊥AE,交AE的延长线于点D.
(1)、如图1,若a=6,∠B=45°,∠C=75°,求b的值;(2)、某公园准备在园内一个锐角三角形水池ABC中建一座小型景观桥CD(如图2所示),若CD⊥AB,AC=14米,AB=10米,sin∠ACB= ,求景观桥CD的长度.25. 如图1,AB是⊙O的直径,点E是⊙O上一动点,且不与A,B两点重合,∠EAB的平分线交⊙O于点C,过点C作CD⊥AE,交AE的延长线于点D. (1)、求证:CD是⊙O的切线;(2)、求证:AC2=2AD•AO;(3)、如图2,原有条件不变,连接BE,BC,延长AB至点M,∠EBM的平分线交AC的延长线于点P,∠CAB的平分线交∠CBM的平分线于点Q.求证:无论点E如何运动,总有∠P=∠Q.26. 已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).(1)、若二次函数的图象经过点(0,4),对称轴为x=1,求此二次函数的表达式;(2)、若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;(3)、记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1 , 求实数m的最小值.
(1)、求证:CD是⊙O的切线;(2)、求证:AC2=2AD•AO;(3)、如图2,原有条件不变,连接BE,BC,延长AB至点M,∠EBM的平分线交AC的延长线于点P,∠CAB的平分线交∠CBM的平分线于点Q.求证:无论点E如何运动,总有∠P=∠Q.26. 已知关于x的二次函数y1=x2+bx+c(实数b,c为常数).(1)、若二次函数的图象经过点(0,4),对称轴为x=1,求此二次函数的表达式;(2)、若b2﹣c=0,当b﹣3≤x≤b时,二次函数的最小值为21,求b的值;(3)、记关于x的二次函数y2=2x2+x+m,若在(1)的条件下,当0≤x≤1时,总有y2≥y1 , 求实数m的最小值.