湖南省郴州市2021年中考数学试卷
试卷更新日期:2021-08-24 类型:中考真卷
一、选择题(共8小题,每小题3分,共24分)
-
1. 实数a,b在数轴上的位置如图所示,则下列式子正确的是( )
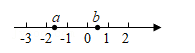 A、a>b B、|a|>|b| C、ab>0 D、a+b>02. 下列垃圾分类图标分别表示:“可回收垃圾”、“有害垃圾”、“厨余垃圾”、“其它垃圾”,其中既是轴对称图形,又是中心对称图形的是( )A、
A、a>b B、|a|>|b| C、ab>0 D、a+b>02. 下列垃圾分类图标分别表示:“可回收垃圾”、“有害垃圾”、“厨余垃圾”、“其它垃圾”,其中既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 为响应习近平总书记“坚决打赢关键核心技术攻坚战”的号召,某科研团队最近攻克了7nm的光刻机难题,其中1nm=0.000000001m,则7nm用科学记数法表示为( )A、0.7×108m B、7×10﹣8m C、0.7×10﹣8m D、7×10﹣9m4. 下列运算正确的是( )A、a2•a3=a6 B、(a3)2=a5 C、 =3 D、(a+b)2=a2+b25. 下列说法正确的是( )A、“明天下雨的概率为80%”,意味着明天有80%的时间下雨 B、经过有信号灯的十字路口时,可能遇到红灯,也可能遇到绿灯 C、“某彩票中奖概率是1%”,表示买100张这种彩票一定会有1张中奖 D、小明前几次的数学测试成绩都在90分以上这次数学测试成绩也一定在90分以上6. 已知二元一次方程组 ,则x﹣y的值为( )A、2 B、6 C、﹣2 D、﹣67. 由5个相同的小立方体搭成的物体如图所示,则它的俯视图为( )
3. 为响应习近平总书记“坚决打赢关键核心技术攻坚战”的号召,某科研团队最近攻克了7nm的光刻机难题,其中1nm=0.000000001m,则7nm用科学记数法表示为( )A、0.7×108m B、7×10﹣8m C、0.7×10﹣8m D、7×10﹣9m4. 下列运算正确的是( )A、a2•a3=a6 B、(a3)2=a5 C、 =3 D、(a+b)2=a2+b25. 下列说法正确的是( )A、“明天下雨的概率为80%”,意味着明天有80%的时间下雨 B、经过有信号灯的十字路口时,可能遇到红灯,也可能遇到绿灯 C、“某彩票中奖概率是1%”,表示买100张这种彩票一定会有1张中奖 D、小明前几次的数学测试成绩都在90分以上这次数学测试成绩也一定在90分以上6. 已知二元一次方程组 ,则x﹣y的值为( )A、2 B、6 C、﹣2 D、﹣67. 由5个相同的小立方体搭成的物体如图所示,则它的俯视图为( ) A、
A、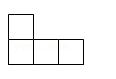 B、
B、 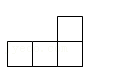 C、
C、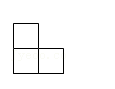 D、
D、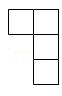 8. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( )
8. 如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是( ) A、
A、 B、
B、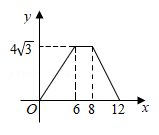 C、
C、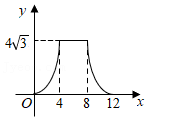 D、
D、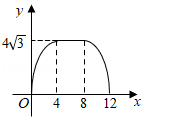
二、填空题(共8小题,每小题3分,共24分)
-
9. 使 有意义的x的取值范围是 .10. 在反比例函数y= 的图象的每一支曲线上,函数值y随自变量x的增大而增大,则m的取值范围是 .11. 为庆祝中国共产党建党一百周年,某校开展了主题为“我身边的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得分按4:3:3的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别为95分、80分、90分,则选手甲的最终得分为 分.12. 一个多边形的每一个外角都等于60°,则这个多边形的内角和为 度.13. 关于x的一元二次方程x2﹣5x+m=0有两个相等的实数根,则m=.14. 如图是一架梯子的示意图,其中AA1∥BB1∥CC1∥DD1 , 且AB=BC=CD.为使其更稳固,在A,D1间加绑一条安全绳(线段AD1)量得AE=0.4m,则AD1=m.
 15. 如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是 cm2(结果用含π的式子表示).
15. 如图,方老师用一张半径为18cm的扇形纸板,做了一个圆锥形帽子(接缝忽略不计).如果圆锥形帽子的半径是10cm,那么这张扇形纸板的面积是 cm2(结果用含π的式子表示).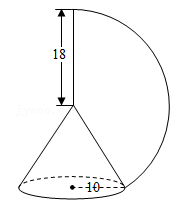 16. 如图,在△ABC中,AB=5,AC=4,sinA= ,BD⊥AC交AC于点D.点P为线段BD上的动点,则PC+ PB的最小值为 .
16. 如图,在△ABC中,AB=5,AC=4,sinA= ,BD⊥AC交AC于点D.点P为线段BD上的动点,则PC+ PB的最小值为 .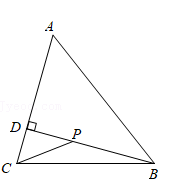
三、解答题(17~19题每题6分,20~23题每题8分,24~25题每题10分,26题12分,共82分)
-
17. 计算:(2021﹣π)0﹣|2﹣ |+( )﹣1•tan60°.18. 先化简,再求值:( ﹣ )÷ ,其中a= .19. 如图,四边形ABCD中,AB=DC,将对角线AC向两端分别延长至点E,F,使AE=CF.连接BE,DF,若BE=DF.证明:四边形ABCD是平行四边形.
 20. 我市为加快推进生活垃圾分类工作,对分类垃圾桶实行统一的外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾用绿色收集桶,其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况,某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据调查结果,绘制了如图所示的两幅不完整的统计图.
20. 我市为加快推进生活垃圾分类工作,对分类垃圾桶实行统一的外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾用绿色收集桶,其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况,某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据调查结果,绘制了如图所示的两幅不完整的统计图.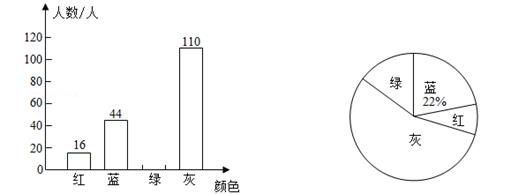
根据图中信息,解答下列问题:
(1)、此次调查一共随机采访了 名学生,在扇形统计图中,“灰”所在扇形的圆心角的度数为 度;(2)、补全条形统计图(要求在条形图上方注明人数);(3)、若该校有3600名学生,估计该校学生将用过的餐巾纸投放到红色收集桶的人数;(4)、李老师计划从A,B,C,D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛,请用树状图法或列表法求出恰好抽中A,B两人的概率.21. 如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣小组为测算电梯AC的高度,测得斜坡AB=105米,坡度i=1:2,在B处测得电梯顶端C的仰角α=45°,求观光电梯AC的高度.(参考数据: ≈1.41, ≈1.73, ≈2.24.结果精确到0.1米)
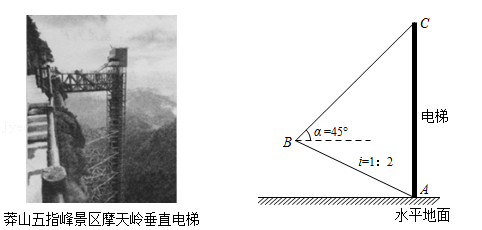 22. “七•一”建党节前夕,某校决定购买A,B两种奖品,用于表彰在“童心向党”活动中表现突出的学生.已知A奖品比B奖品每件多25元,预算资金为1700元,其中800元购买A奖品,其余资金购买B奖品,且购买B奖品的数量是A奖品的3倍.(1)、求A,B奖品的单价;(2)、购买当日,正逢该店搞促销活动,所有商品均按原价八折销售,故学校调整了购买方案:不超过预算资金且购买A奖品的资金不少于720元,A,B两种奖品共100件,求购买A,B两种奖品的数量,有哪几种方案?23. 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,点D是 的中点,DE∥BC交AC的延长线于点E.
22. “七•一”建党节前夕,某校决定购买A,B两种奖品,用于表彰在“童心向党”活动中表现突出的学生.已知A奖品比B奖品每件多25元,预算资金为1700元,其中800元购买A奖品,其余资金购买B奖品,且购买B奖品的数量是A奖品的3倍.(1)、求A,B奖品的单价;(2)、购买当日,正逢该店搞促销活动,所有商品均按原价八折销售,故学校调整了购买方案:不超过预算资金且购买A奖品的资金不少于720元,A,B两种奖品共100件,求购买A,B两种奖品的数量,有哪几种方案?23. 如图,△ABC是⊙O的内接三角形,AC是⊙O的直径,点D是 的中点,DE∥BC交AC的延长线于点E.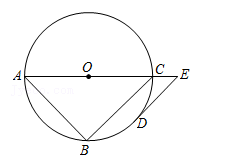 (1)、求证:直线DE与⊙O相切;(2)、若⊙O的直径是10,∠A=45°,求CE的长.24. 某商店从厂家以每件2元的价格购进一批商品,在市场试销中发现,此商品的月销售量y(单位:万件)与销售单价x(单位元)之间有如下表所示关系:
(1)、求证:直线DE与⊙O相切;(2)、若⊙O的直径是10,∠A=45°,求CE的长.24. 某商店从厂家以每件2元的价格购进一批商品,在市场试销中发现,此商品的月销售量y(单位:万件)与销售单价x(单位元)之间有如下表所示关系:x
…
4.0
5.0
5.5
6.5
7.5
…
y
…
8.0
6.0
5.0
3.0
1.0
…
(1)、根据表中的数据,在如图中描出实数对(x,y)所对应的点,并画出y关于x的函数图象;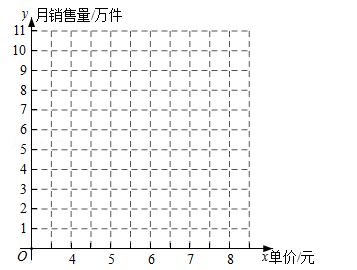 (2)、根据画出的函数图象,求出y关于x的函数表达式;(3)、设经营此商品的月销售利润为P(单位:万元),
(2)、根据画出的函数图象,求出y关于x的函数表达式;(3)、设经营此商品的月销售利润为P(单位:万元),①写出P关于x的函数表达式;
②该商店计划从这批商品获得的月销售利润为10万元(不计其它成本),若物价局限定商品的销售单价不得超过进价的200%,则此时的销售单价应定为多少元?
25. 如图1,在等腰直角三角形ABC中,∠BAC=90°,点E,F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),将线段AH绕点A逆时针方向旋转90°得到AG,连接GC,HB.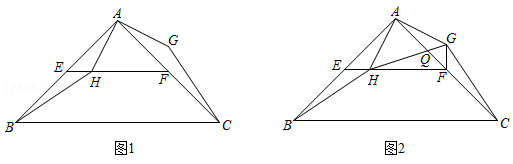 (1)、证明:△AHB≌△AGC;(2)、如图2,连接GF,HG,HG交AF于点Q.
(1)、证明:△AHB≌△AGC;(2)、如图2,连接GF,HG,HG交AF于点Q.①证明:在点H的运动过程中,总有∠HFG=90°;
②若AB=AC=4,当EH的长度为多少时△AQG为等腰三角形?
26. 将抛物线y=ax2(a≠0)向左平移1个单位,再向上平移4个单位后,得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(﹣3,0),点P是抛物线H上的一个动点.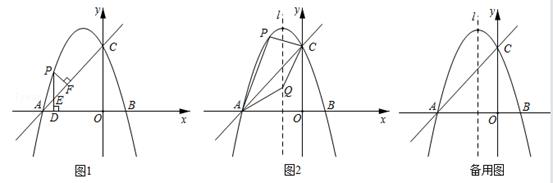 (1)、求抛物线H的表达式;(2)、如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)、如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
(1)、求抛物线H的表达式;(2)、如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)、如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.