湖北省枣阳市2021年数学中考模拟试卷

试卷更新日期：2021-08-24 类型：中考模拟

进入出卷网下载

一、单选题

1. -2021的相反数是（）

A、2021 B、-2021 C、 $\frac{1}{2021}$ D、 $- \frac{1}{2021}$

查看试题解析
2. 如图，将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上，若∠2=64°，则∠1的大小为（）

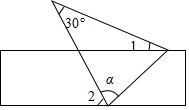A、90°﹣α B、α﹣64° C、34° D、36°

查看试题解析
3. 如图正方体的平面展开图可知，原正方体“喜”字所在面的对面的汉字是（）

A、建 B、党 C、百 D、年

查看试题解析
4. 《孙子算经》是中国古代重要的数学著作，纸书大约在一千五百年前，其中一道题，原文是：“今三人共车，两车空；二人共车，九人步．问人与车各几何？”意思是：现有若干人和车，若每辆车乘坐3人，则空余两辆车：若每辆车乘坐2人，则有9人步行，问人与车各多少？设有x人，y辆车，可列方程组为（）

A、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x}{2} + 9 = y \end{array}$ B、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x - 9}{2} = y \end{array}$ C、 ${\begin{array}{l} \frac{x}{3} = y + 2 \\ \frac{x - 9}{2} = y \end{array}$ D、 ${\begin{array}{l} \frac{x}{3} = y - 2 \\ \frac{x}{2} - 9 = y \end{array}$

查看试题解析
5. 不等式组 ${\begin{array}{l} 5 x + 2 > 3 (x - 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$ 的所有非负整数解的和是（）

A、 $10$ B、 $7$ C、 $6$ D、 $0$

查看试题解析
6. 如图是二次函数y=ax²+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是直线x=1，下列结论正确的是（）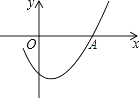

A、b²＜4ac B、ac＞0 C、2a﹣b=0 D、a﹣b+c=0

查看试题解析

二、填空题

7. 如图，BC是⊙O的弦，OA⊥BC，∠OBC＝20°，则∠ADC的度数是.

查看试题解析
8. 有一个数值转换机，原理如下：

当输入的 $x = 81$ 时，输出的 $y =$ .

查看试题解析
9. 如图，∠ABD＝∠BCD＝90°，DB平分∠ADC，过点B作BM∥CD交AD于M.连接CM交DB于 N.若CD＝6，AD＝8，求MN的长为 .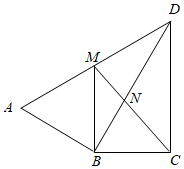

查看试题解析

三、解答题

10. 如图，某小区有甲、乙两座楼房，楼间距BC为60米，在乙楼顶部A点测得甲楼顶部D点的仰角为27°，在乙楼底部B点测得甲楼顶部D点的仰角为45°，则乙楼的高度为多少米？（结果精确到1米，sin27°≈0.45，cos27°≈0.9，tan27°≈0.51）

查看试题解析
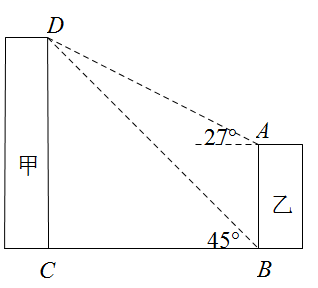11. 如图，BD是菱形ABCD的对角线，∠CBD＝70°.

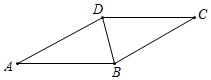(1)、请用尺规作图法，作AB的垂直平分线EF，垂足为E，交AD于F；（不写作法，保留作图痕迹）

(2)、在（1）条件下，连接BF，求∠DBF的度数.

查看试题解析

12. 为响应国家节能减排、垃圾分类政策，某地制定出台了《生活垃圾分类管理办法》，旨在加强生活垃圾分类管理，提高生活垃圾减量化、资源化、无害化处置水平及推进生态文明建设.某校为了解学生对垃圾分类知识的掌握情况，对九年级甲、乙两班各60名学生进行知识测试(满分60分)，测试完成后分别抽取了12份成绩，整理分析过程如下：

（收集数据）甲班12名学生测试成绩统计如下：45，59，60，38，57，53，52，58，60，50，43，49.

乙班12名学生测试成绩不低于40但低于50分的成绩如下：46，47，43，42，47.

（整理数据）按如下分数段整理、描述这两组样本数据：

组别/频数	35≤x<40	40≤x<45	45≤x<50	50≤x<55	55≤x<60
甲	1	1	2	x	5
乙	2	2	3	1	4

（分析数据）两组样本数据的平均数、众数、中位数、方差如表：

班级	平均数	众数	中位数	方差
甲	52	60	52.5	52.54
乙	48.7	47	y	67.51

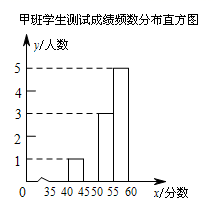(1)、根据以上信息，可以求出：x＝ ▲ ，y＝ ▲ ，并补全频数分布直方图.

(2)、若规定得分在40分及以上为合格，估计参加知识测试的学生中合格的学生共有人.

(3)、你认为哪个班的学生知识测试的整体成绩较好？请说明理由.

查看试题解析

13. 在初中阶段的函数学习中，我们经历了“确定函数的表达式－→利用函数图象研究其性质－→运用函数解决问题”的学习过程.在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象.九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究了函数

y = | \frac{- 2}{x + 1} |

的图象与性质.其探究过程如下，绘制函数图象，如图.

(1)、①列表：下表是

x

与

y

的几组对应值，其中

m

＝；

$x$	…	－4	－3	－2	$- \frac{3}{2}$	$- \frac{1}{2}$	0	1	2	…
$y$	…	$\frac{2}{3}$	1	2	4	4	2	$m$	$\frac{2}{3}$	…

②描点：根据表中各组对应值( $x$ ， $y$ )，在平面直角坐标系中描出了各点；
③连线：用平滑的曲线顺次连接各点，画出了部分图象，请你把图象补充完整；

(2)、通过观察图象，写出该函数的两条性质：①；②.

查看试题解析

14. 如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连结BE.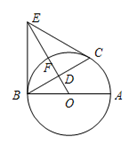

(1)、求证：BE是⊙O的切线；

(2)、设OE交⊙O于点F，若DF＝2，BC＝ $4 \sqrt{3}$ ，求劣弧BC的长.

查看试题解析
15. 在 $△$ ABC中，∠ABC＝90°， $\frac{A B}{B C} = n$ ，M是BC上一点，连接AM.

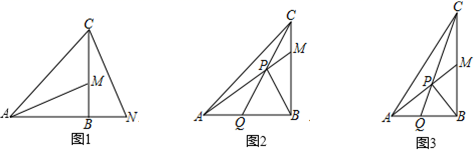(1)、如图1，若n＝1，N是AB延长线上一点，CN与AM垂直，求证：BM＝BN.

(2)、过点B作BP⊥AM，P为垂足，连接CP并延长交AB于点Q.
①如图2，若n＝1，求证： $\frac{C P}{P Q} = \frac{B M}{B Q}$ .

②如图3，若M是BC的中点，求tan∠BPQ的值.（用含n的式子表示）

查看试题解析
16. 如图，抛物线 $y = - x^{2} + b x + 5$ 与x轴交于A，B两点．

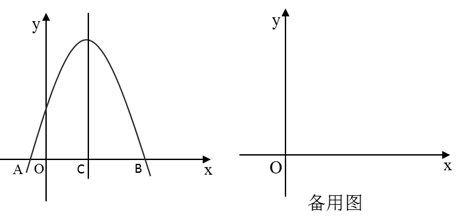(1)、若过点C的直线 $x = 2$ 是抛物线的对称轴．
①求抛物线的解析式；

②对称轴上是否存在一点P，使点B关于直线 $O P$ 的对称点 $B^{'}$ 恰好落在对称轴上．若存在，请求出点P的坐标；若不存在，请说明理由．

(2)、当 $b \geq 4$ ， $0 \leq x \leq 2$ 时，函数值y的最大值满足 $3 \leq y \leq 15$ ，求b的取值范围．

查看试题解析