河南省汝阳县2021年数学中考二模试卷
试卷更新日期:2021-08-24 类型:中考模拟
一、单选题
-
1. 的绝对值为( )A、6 B、-6 C、 D、2. 下面立体图形中,从左面看到的平面图形与其他三个不一样的是( ).A、
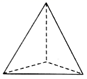 B、
B、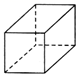 C、
C、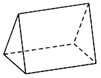 D、
D、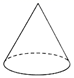 3. 下列调查中,适合抽样调查的是( ).A、调查本班同学的体育达标情况 B、了解“嫦娥五号”探测器的零部件状况 C、疫情期间,了解全校师生入校时体温情况 D、调查黄河的水质情况4. 七巧板是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪.为祝贺辛丑年的到来,用一副七巧板(如图①),拼成了“牛气冲天”的图案(如图②),则图②中 ( ).
3. 下列调查中,适合抽样调查的是( ).A、调查本班同学的体育达标情况 B、了解“嫦娥五号”探测器的零部件状况 C、疫情期间,了解全校师生入校时体温情况 D、调查黄河的水质情况4. 七巧板是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪.为祝贺辛丑年的到来,用一副七巧板(如图①),拼成了“牛气冲天”的图案(如图②),则图②中 ( ).
 A、360° B、270° C、225° D、180°5. 计算: ,其中第一步运算的依据是( ).A、幂的乘方法则 B、乘法分配律 C、积的乘方法则 D、同底数幂的乘法法则6. , 两点在反比例函数图象上的位置如图所示,两点的坐标分别为 , ,下列结论正确的是( ).
A、360° B、270° C、225° D、180°5. 计算: ,其中第一步运算的依据是( ).A、幂的乘方法则 B、乘法分配律 C、积的乘方法则 D、同底数幂的乘法法则6. , 两点在反比例函数图象上的位置如图所示,两点的坐标分别为 , ,下列结论正确的是( ). A、 B、 C、 D、7. 当 时,关于 的一元二次方程 的根的情况为( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有实数根8. 2018年7月,郑州龙子湖智慧岛开通河南省首个5G基站,2020年全省已累计建成5G基站 万个,规划到2022年5G基站数量将达到 万个.设2020年至2022年5G基站建设的年平均增长率为 ,可列方程为( ).A、 B、 C、 D、9. 在平面直角坐标系中,平行四边形 的边 在 轴上,顶点 , ,对角线 、 相交于点 、分别以点 、 为圆心,以大于 长为半径画弧,两弧交于点 ,连接 交 于点 ,则点 的横坐标为( ).
A、 B、 C、 D、7. 当 时,关于 的一元二次方程 的根的情况为( ).A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、有实数根8. 2018年7月,郑州龙子湖智慧岛开通河南省首个5G基站,2020年全省已累计建成5G基站 万个,规划到2022年5G基站数量将达到 万个.设2020年至2022年5G基站建设的年平均增长率为 ,可列方程为( ).A、 B、 C、 D、9. 在平面直角坐标系中,平行四边形 的边 在 轴上,顶点 , ,对角线 、 相交于点 、分别以点 、 为圆心,以大于 长为半径画弧,两弧交于点 ,连接 交 于点 ,则点 的横坐标为( ). A、5 B、4 C、3 D、110. 如图①,在等边三角形 中,点 是边 上一动点(不与点 , 重合),以 为边向右作等边 ,边 与 相交于点 ,设 , ,若 与 的函数关系的大致图象如图②所示,则等边三角形 的面积为( ).
A、5 B、4 C、3 D、110. 如图①,在等边三角形 中,点 是边 上一动点(不与点 , 重合),以 为边向右作等边 ,边 与 相交于点 ,设 , ,若 与 的函数关系的大致图象如图②所示,则等边三角形 的面积为( ).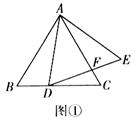
 A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
11. .12. 不等式组 的最小整数解为.13. 郑小舟在数学课本“读一读”中了解到一些中国古代的数学著作,如《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》,现在他计划从这四部书中随机选择两部书购买则选择到《九章算术》的概率是.14. 如图,在扇形 中, ,点 是 的中点,以 为边作矩形 ,点 在弧 上,连接 交 于点 .若 ,则图中阴影部分的面积为.
 15. 如图,矩形 中, , ,点 是 的中点,点 是直线 上的一动点,将 沿 所在直线翻折,得到 ,则 长的最小值是.
15. 如图,矩形 中, , ,点 是 的中点,点 是直线 上的一动点,将 沿 所在直线翻折,得到 ,则 长的最小值是.
三、解答题
-
16. 先化简,再求值: ,其中 .17. 2021年央视春晚,数十个节目给千家万户送上了丰富的“年夜大餐”.中原人民再次以丰富的节目参与到这场全国人民的关注的除夕盛宴中.某校随机对九年级部分学生进行了一次调查,对最喜欢相声《年三十的歌》(记为 )、歌曲《牛起来》(记为 )、武术表演《天地英雄》(记为 )、小品《开往春天的幸福》(记为 )的同学进行了统计(每位同学只选择一个最喜欢的节目),绘制了以下不完整的统计图,请根据图中信息解答问题:
 (1)、本次接受调查的学生共有名;(2)、扇形统计图中, 所在扇形的圆心角度数是;(3)、将条形统计图补充完整;(4)、若九年级共有720名学生,估计其中最喜欢相声《年三十的歌》的学生大约有多少人?18. 千玺广场举办的灯光秀是郑州一景,夜幕下的“大玉米”流灯溢彩,绚丽纷呈.象征着古老河南、厚重河南的“大玉米”,穿上了“晚礼服”,展示着开放河南、出彩河南的崭新形象.如图所示,在 处测得“中原更出彩”顶端 点的仰角为45°,点 到玉米楼顶端 点的距离约为 ,再沿 方向前进 到达 处,测得玉米楼顶端 点的仰角为 .求玉米楼 的总高度.(结果精确到 .参考数据: , , )
(1)、本次接受调查的学生共有名;(2)、扇形统计图中, 所在扇形的圆心角度数是;(3)、将条形统计图补充完整;(4)、若九年级共有720名学生,估计其中最喜欢相声《年三十的歌》的学生大约有多少人?18. 千玺广场举办的灯光秀是郑州一景,夜幕下的“大玉米”流灯溢彩,绚丽纷呈.象征着古老河南、厚重河南的“大玉米”,穿上了“晚礼服”,展示着开放河南、出彩河南的崭新形象.如图所示,在 处测得“中原更出彩”顶端 点的仰角为45°,点 到玉米楼顶端 点的距离约为 ,再沿 方向前进 到达 处,测得玉米楼顶端 点的仰角为 .求玉米楼 的总高度.(结果精确到 .参考数据: , , )
 19. 春暖花开的季节最适合外出摘草莓,不仅能尝到新鲜的草莓,还可以体会田园乐趣,现有甲、乙两家草莓采摘园均推出了优惠活动方案,两家草莓品质相同,且其门票及草莓的销售价格也相同.
19. 春暖花开的季节最适合外出摘草莓,不仅能尝到新鲜的草莓,还可以体会田园乐趣,现有甲、乙两家草莓采摘园均推出了优惠活动方案,两家草莓品质相同,且其门票及草莓的销售价格也相同.甲采摘园的优惠方案是:游客进园需购买门票,采摘的草莓按售价的五折销售.
乙采摘园的优惠方案是:游客进园不需要购买门票,采摘的草莓按售价的七折销售;
优惠期间,设某一位游客的草莓采摘量为 千克,在甲采摘园所需总费用为 元,且 ,在乙采摘园所需总费用为 元,且 .其函数图象如图所示.
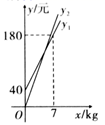 (1)、求 和 的值,并说出它们的实际意义;(2)、求打折前的每千克草莓的售价和 的值;(3)、若预计采摘草莓4千克,那么选择哪家采摘园更省钱?说明理由.20. 我们知道,直线与圆有三种位置关系:相交、相切、相离.当直线与圆有两个公共点(即直线与圆相交)时,这条直线就叫做圆的割线.割线也有一些相关的定理.比如,割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等.下面给出了不完整的定理“证明一”,请补充完整.
(1)、求 和 的值,并说出它们的实际意义;(2)、求打折前的每千克草莓的售价和 的值;(3)、若预计采摘草莓4千克,那么选择哪家采摘园更省钱?说明理由.20. 我们知道,直线与圆有三种位置关系:相交、相切、相离.当直线与圆有两个公共点(即直线与圆相交)时,这条直线就叫做圆的割线.割线也有一些相关的定理.比如,割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等.下面给出了不完整的定理“证明一”,请补充完整.

已知:如图①,过 外一点 作 的两条割线,一条交 于 、 点,另一条交 于 、 点.
求证: .
证明一:连接 、 ,
∵ 和 为 所对的圆周角,∴_▲_.
又∵ ,∴_▲_,∴_▲_.
即 .
研究后发现,如图②,如果连接 、 ,即可得到学习过的圆内接四边形 .那么或许割线定理也可以用圆内接四边形的性质来证明.请根据提示,独立完成证明二.
证明二:连接 、 ,
21. 在平面直角坐标系中,抛物线 经过点 和 .(1)、求 的值及 , 满足的关系式;(2)、若抛物线在 , 两点间从左到右下降,求 的取值范围;(3)、结合函数图象判断,抛物线能否同时经过点 、 ?若能,写出一个符合要求的抛物线的表达式和 的值,若不能,请说明理由.22. 郑小舟在学习中遇到这样一个问题:“如图①,菱形 的边长是4, ,点 为对角线 上一动点,过点 作 ,交边 、 于点 、 ,把 沿 折叠得到 ,若 恰为等腰三角形,求 的长.”他尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整: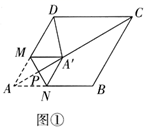
 (1)、根据点 在 上的不同位置,画出相应的图形,测量线段 , 的长度,得到下表几组对应值.
(1)、根据点 在 上的不同位置,画出相应的图形,测量线段 , 的长度,得到下表几组对应值.0
0.5
1.0
1.5
2.0
2.5
3.0
4.0
3.18
2.48
2.06
2.07
2.53
3.23
操作中发现:“线段 的长度无需测量即可得到”.因为 与 满足关系式:.
(2)、将线段 的长度作为自变量 , 的长度是 的函数,记作 ,在图②所示的平面直角坐标系中画出函数 的图象.(3)、设 , ,继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数, ).23. 如图1,在 中, , ,点 、 分别在边 、 上, ,连接 .将 绕点 顺时针方向旋转,记旋转角为 .

 (1)、(问题发现)
(1)、(问题发现)①当 时, ;②当 时, ;
(2)、(拓展研究)试判断:当 时, 的大小有无变化?请仅就图2的情形给出证明;
(3)、(问题解决)在旋转过程中,求出 的最大值.