河南省濮阳市2021年数学中考一模试卷

试卷更新日期：2021-08-24 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2020的倒数是（）

A、﹣2020 B、﹣ $\frac{1}{2020}$ C、2020 D、 $\frac{1}{2020}$

查看试题解析
2. 分别观察下列几何体，其中主视图、左视图和俯视图完全相同的是（）

A、圆锥 B、圆柱 C、三棱柱 D、正方体

查看试题解析
3. 下列采用的调查方式中，不合适的是（）

A、了解澧水河的水质，采用抽样调查． B、了解一批灯泡的使用寿命，采用全面调查． C、了解张家界市中学生睡眠时间，采用抽样调查． D、了解某班同学的数学成绩，采用全面调查．

查看试题解析
4. 一副直角三角板如图放置，点C在FD的延长线上，AB//CF，∠F=∠ACB=90°，则∠DBC的度数为（）

A、10° B、15° C、18° D、30°

查看试题解析
5. 下列运算正确的是（）

A、 $3 a^{2} + 2 a = 5 a^{2}$ B、 $- 8 a^{2} \div 4 a = 2 a^{6}$ C、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$ D、 $4 a^{3} \cdot 3 a^{2} = 12 a^{6}$

查看试题解析
6. 若二次函数 $y = x^{2} - 4 x + 3$ 的图象经过 $A (- 2 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (4 ， y_{3})$ 三点，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{3} < y_{1}$ D、 $y_{3} < y_{1} < y_{2}$

查看试题解析
7. 下列一元二次方程中，有两个不相等实数根的是（）

A、 $x^{2} - x + \frac{1}{4} = 0$ B、x²+2x+4=0 C、x²-x+2=0 D、x²-2x=0

查看试题解析
8. 现有两个不透明的袋子，一个装有2个红球、1个白球，另一个装有1个黄球、2个红球，这些球除颜色外完全相同，从两个袋子中各随机摸出1个球，摸出的两个球颜色相同的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{4}{9}$ C、 $\frac{3}{5}$ D、 $\frac{2}{3}$

查看试题解析
9. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
10. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ，过点 $D$ 作 $D H ⊥ A B$ 于点 $H$ ，连接 $O H$ ，若 $O A = 3$ ， $O H = 2$ .则菱形 $A B C D$ 的面积为（）

A、12 B、10 C、6 D、24

查看试题解析

二、填空题

11. 写出一个负数，使这个数的绝对值小于4.

查看试题解析
12. 如图，数轴上不等式组的解集可以表示为.

查看试题解析
13. 如图，将周长为10的 $△ A B C$ 沿 $B C$ 边向右平移3个单位，得到 $△ D E F$ ，则四边形 $A B F D$ 的周长为.

查看试题解析
14. 如图，菱形 $A B C D$ 的边长为17，对角线 $A C = 30$ ，点 $E$ 、 $F$ 分别是边 $C D$ 、 $B C$ 的中点，连接 $E F$ 并延长与 $A B$ 的延长线相交于点 $G$ ，则 $E G =$ .

查看试题解析
15. 如图，正方形 $A B C D$ 的边长为8，点 $E$ 在 $A B$ 上， $B E = 2$ ， $F$ 为对角线 $A C$ 上一动点，则 $△ B F E$ 周长的最小值为.

查看试题解析

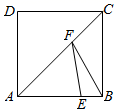
三、解答题

16. 先化简，再求值： $\frac{m}{m^{2} - 9} \div (1 + \frac{3}{m - 3})$ ，其中 $m = - 4$ .

查看试题解析
17. 每年12月4日是“国家宪法日”.某中学为了让学生学宪法，成为宪法小卫士，组织全校学生参加了“宪法知识网络答题”活动，该校德育处对九年级全体学生答题成绩进行统计，将成绩分为四个等级：优秀、良好、一般、不合格；并绘制成如下不完整的统计图.

请你根据图（1）图（2）中所给的信息解答下列问题：

(1)、该校九年级共有名学生，“优秀”所占圆心角的度数为.

(2)、请将图17（1）中的条形统计图补充完整.

(3)、已知该市共有20000名学生参加了这次“宪法知识网络答题”活动，请以该校九年级学生答题成绩统情况估计该市大约有多少名学生在这次答题中成绩不合格？

查看试题解析
18. 某市为了加快5G网络信号覆盖，在市区附近小山顶架设信号发射塔，如图，山顶上有一个信号塔 $A C$ ，已知信号塔高 $A C = 21$ 米，在山脚下点 $B$ 处测得塔底 $C$ 的仰角 $∠ C B D = 36.9 °$ ，塔顶 $A$ 的仰角 $∠ A B D = 42.0 °$ ，求山高 $C D$ （点 $A$ ， $C$ ， $D$ 在同一条竖直线上）.（参考数据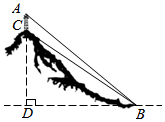： $\tan 36.9 ° \approx 0.75$ ， $\sin 36.9 ° \approx 0.60$ ， $\tan 42.0 ° \approx 0.90$ .）

查看试题解析
19. 某商店准备购进 $A$ 、B两种商品， $A$ 种商品每件的进价比 $B$ 种商品每件的进价多20元，购进3件 $A$ 种商品和2件 $B$ 种商品共需210元.

(1)、 $A$ 种商品每件的进价和 $B$ 种商品每件的进价各是多少元？

(2)、商店计划用不超过1560元的资金购进 $A$ 、 $B$ 两种商品共40件，其中 $A$ 种商品的数量不低于14件，该商店有几种进货方案？

查看试题解析
20. 如图， $A B$ 为 $⊙ O$ 的直径，点 $C$ 是 $⊙ O$ 上一点， $C D$ 与 $⊙ O$ 相切于点 $C$ ，过点 $A$ 作 $A D ⊥ D C$ ，交半圆 $O$ 于点 $E$ ，连接 $A C$ ， $B C$ .

(1)、求证： $A C$ 是 $∠ D A B$ 的角平分线；

(2)、若 $A D = 2$ ， $A B = 3$ ，求 $A C$ 的长；

(3)、若 $A E = 2 D E$ ，试判断以 $O$ ， $A$ ， $E$ ， $C$ 为顶点的四边形的形状为.

查看试题解析
21. 已知抛物线 $y = a x^{2} + b x + c$ 与 $y$ 轴交于点 $(0 ， 3 a)$ ，对称轴为 $x = 1$ .

(1)、试用含 $a$ 的代数式表示 $b$ 、 $c$ .

(2)、当抛物线过点 $(2 ， 3)$ 时，求此抛物线的解析式.

(3)、求当 $b (c + 6)$ 取得最大值时的抛物线的顶点坐标.

查看试题解析

22. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究函数

y = \frac{3}{| x |}

的图象与性质.其探究过程如下：

(1)、绘制函数图象，如图.

列表：下表是 $x$ 与 $y$ 的几组对应值，其中 $m =$ ；

$x$	…	-3	-2	-1	$- \frac{1}{3}$	$\frac{1}{3}$	1	2	3	…
$y$	…	1	$\frac{3}{2}$	3	9	9	3	$m$	1	…

描点：根据表中各组对应值 $(x ， y)$ ，在平面直角坐标系中描出了各点：

连线：用平滑的曲线顺次连接各点，画出了部分图象，请你把图象补充完整；

(2)、通过观察图象，写出该函数的两条性质：①；②；

(3)、①观察发现：若直线

y = 3

交函数

y = \frac{3}{| x |}

的图象于

A

，

B

两点，连接

O A

，过点

B

作

B C // O A

交

x

轴于

C

，则

S_{四 边 形 O A B C} =

；

②探究思考：将①中“直线 $y = 3$ ”改为“直线 $y = a (a > 0)$ ”，其他条件不变，则 $S_{四边形 O A B C} =$ ；

③类比猜想：若直线 $y = a (a > 0)$ 交函数 $y = \frac{k}{| x |} (k > 0)$ 的图象于 $A$ ， $B$ 两点，连接 $O A$ ，过点 $B$ 作 $B C // O A$ 交轴于 $C$ ，则 $S_{四边形 O A B C} =$ ；

查看试题解析

23. 一次小组合作探究课上，小明将两个正方形按如图1所示的位置摆放（点 $E$ 、 $A$ 、 $D$ 在同一条直线上）.

(1)、发现 $B E$ 与 $D G$ 数量关系是， $B E$ 与 $D G$ 的位置关系是.

(2)、将正方形 $A E F G$ 绕点 $A$ 按逆时针方向旋转（如图2），（1）中的结论还成立吗？若能，请给出证明；若不能，请说明理由.

(3)、把图1中的正方形分别改写成矩形 $A E F G$ 和矩形 $A B C D$ ，且 $\frac{A E}{A G} = \frac{A B}{A D} = \frac{2}{3}$ ， $A E = 2$ ， $A B = 4$ ，将矩形 $A E F G$ 绕点 $A$ 按顺时针方向旋转（如图3），连接 $D E$ ， $B G$ .小组发现：在旋转过程中， $D E^{2} + B G^{2}$ 的值是定值，请直接写出这个定值.

查看试题解析