河南省平顶山市2021年数学第二次中招调研测试试卷
试卷更新日期:2021-08-24 类型:中考模拟
一、单选题
-
1. -2021的绝对值等于( )A、2021 B、-2021 C、 D、2. 下列图形既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 一张厚度为 的足够大的正方形纸,假设能对折24次,那么折纸后的高度就远远超过珠穆朗玛峰.如果将上述正方形纸对折12次,那么折纸后的总厚度为( )A、 B、 C、 D、5. 九(1)班选派5名学生参加演讲比赛,他们的成绩如下:
3. 下列运算正确的是( )A、 B、 C、 D、4. 一张厚度为 的足够大的正方形纸,假设能对折24次,那么折纸后的高度就远远超过珠穆朗玛峰.如果将上述正方形纸对折12次,那么折纸后的总厚度为( )A、 B、 C、 D、5. 九(1)班选派5名学生参加演讲比赛,他们的成绩如下:选手
平均成绩
中位数
成绩/分
86
■
82
88
82
85
■
则上表中被遮盖的两个数据从左到右依次是( )
A、87,86 B、87,87 C、82,86 D、82,876. 某几何体由一些大小相同的小正方体组成,如图是它的俯视图和主视图,那么组成该几何体的小正方体的个数最少为( ) A、4个 B、5个 C、6个 D、7个7. 定义新运算: ,则对于函数 ,下列说法正确的是( )A、当 时, 随 增大而增大 B、函数图象经过点 C、函数图象位于第一、三象限 D、当 时,8. 如图,在 中, , ,以点 为圆心,任意长为半径作弧,分别交边 , 于点 , ;再分别以点 , 为圆心,以大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 .设 , 的面积分别为 , ,则 的值为( )
A、4个 B、5个 C、6个 D、7个7. 定义新运算: ,则对于函数 ,下列说法正确的是( )A、当 时, 随 增大而增大 B、函数图象经过点 C、函数图象位于第一、三象限 D、当 时,8. 如图,在 中, , ,以点 为圆心,任意长为半径作弧,分别交边 , 于点 , ;再分别以点 , 为圆心,以大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 .设 , 的面积分别为 , ,则 的值为( ) A、 B、 C、 D、9. 如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第 个图中所有等腰直角三角形的面积和为( )
A、 B、 C、 D、9. 如图所示,所有的四边形都是正方形,所有三角形都是等腰直角三角形,且最大的正方形的边长为4.若按照图①至图③的规律设计图案,则在第 个图中所有等腰直角三角形的面积和为( )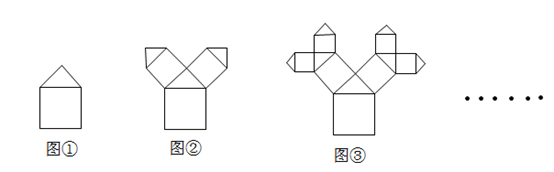 A、 B、 C、 D、3210. 如图,在平面直角坐标系中,直线 分别与 轴、 轴交于 , 两点,在线段 上取一点 ,过 作 轴于 , 轴于 ,连结 ,当 最短时,点 的坐标为( )
A、 B、 C、 D、3210. 如图,在平面直角坐标系中,直线 分别与 轴、 轴交于 , 两点,在线段 上取一点 ,过 作 轴于 , 轴于 ,连结 ,当 最短时,点 的坐标为( )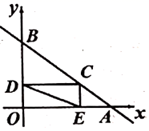 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
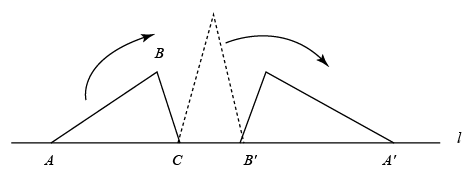
11. 请写出一个比 小的正整数.12. 已知关于 的方程 无实数根,则 满足的条件是.13. 甲袋中装有3个相同的小球,分别写有数字1,2,3;乙袋中装有2个相同的小球,分别写有数字1,2.现从两个袋子中各随机取出1个小球,则取出的两个小球上数字之和为3的概率是.14. 如图,等腰 放置在直线 上, , .将 绕点 旋转,使点 的对应点 落在直线 上,再将第一次旋转得到的三角形绕点 继续旋转,使其顶点 落在直线 上点 处,则点 经过的路径总长为(结果保留 ).
 15. 如图,在矩形 中, , , 的角平分线交边 于点 , 于点 ,连结 并延长分别交 , 于点 , .给出下列结论:① ;② ;③ ;④ .其中正确的有.
15. 如图,在矩形 中, , , 的角平分线交边 于点 , 于点 ,连结 并延长分别交 , 于点 , .给出下列结论:① ;② ;③ ;④ .其中正确的有.
三、解答题
-
16. 先化简,再求值: ,其中 为整数且满足不等式组 .17. 某校体育社团为了解本校九年级女生立定跳远达标情况,从九年级女生中随机抽取了25名女生进行了测试,获得立定跳远成绩(单位: )及整理的部分信息如下:
收集数据:142 149 150 153 156 159 160 165 165 165 166 168 168 169 170 174 176 178 178 178 180 182 188 189 197
整理数据:通过计算可知样本平均数为 .
频数分布统计表
分组
频数
1
4
8
2
根据以上信息回答下列问题:
(1)、填空:①上表中 , .②女生立定跳远成绩达到 及以上成绩时为优秀,则样本的优秀率为.
(2)、若本校九年级女生共500人,根据以上数据估计本校九年级女生中立定跳远成绩达到优秀的人数有多少?(3)、经调查可知,今年市区九年级女生立定跳远的整体情况如下:平均分 ,优秀率 .请结合该校抽取的女生的立定跳远成绩的平均数、优秀率和市区九年级女生立定跳远整体情况对比,评估本校九年级女生立定跳远的成绩,并提出相应建议.18. 小明和小亮相约从学校前往博物馆,其中学校距离博物馆900米.小明因有事,比小亮晚一些出发,图中 、 分别是小明、小亮行驶的路程 与小明追赶时间 之间的关系. (1)、观察图象可知,小亮比小明先走了米.(2)、求 、 的值,并解释 的实际意义.(3)、通过计算说明,谁先到博物馆.19. 一渔船跟踪鱼群由西向东航行,在点 处测得北偏东 方向上有一海岛 ,航行10海里后到达 处,又测得海岛 位于北偏东 方向上.
(1)、观察图象可知,小亮比小明先走了米.(2)、求 、 的值,并解释 的实际意义.(3)、通过计算说明,谁先到博物馆.19. 一渔船跟踪鱼群由西向东航行,在点 处测得北偏东 方向上有一海岛 ,航行10海里后到达 处,又测得海岛 位于北偏东 方向上. (1)、求 处到海岛 的距离(结果精确到0.1海里.参考数据: , , , );(2)、已知海岛 的周围20海里范围内有暗礁,若渔船继续由西向东航行是否有触礁危险?说明理由.20. 顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.如图①所示: 切 于点 , 交 于点 , , 就是 的一个弦切角.经研究发现:弦切角等于所夹弧所对的圆周角.下面给出了上述命题的“已知”和“求证”,请写出“证明”过程,并回答后面的问题.
(1)、求 处到海岛 的距离(结果精确到0.1海里.参考数据: , , , );(2)、已知海岛 的周围20海里范围内有暗礁,若渔船继续由西向东航行是否有触礁危险?说明理由.20. 顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.如图①所示: 切 于点 , 交 于点 , , 就是 的一个弦切角.经研究发现:弦切角等于所夹弧所对的圆周角.下面给出了上述命题的“已知”和“求证”,请写出“证明”过程,并回答后面的问题.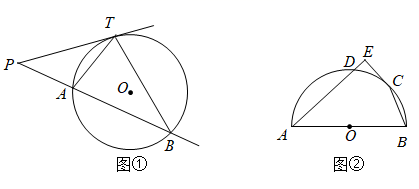 (1)、已知,如图①, 是 的切线, 为切点,射线 交 于 , 两点,连接 , .求证: .(2)、如图②, 为半 的直径, 为圆心, , 为半 上两点,过点 作半 的切线 交 的延长线于点 ,若 ,且 , ,则 .21. 已知,抛物线 与 轴交于点 , 两点( ).
(1)、已知,如图①, 是 的切线, 为切点,射线 交 于 , 两点,连接 , .求证: .(2)、如图②, 为半 的直径, 为圆心, , 为半 上两点,过点 作半 的切线 交 的延长线于点 ,若 ,且 , ,则 .21. 已知,抛物线 与 轴交于点 , 两点( ). (1)、已知 ,求抛物线的解析式及顶点 的坐标;(2)、设点 为抛物线上一点,若 ,且 的纵坐标 满足 ,求代数式 的值;(3)、已知,点 , 为平面直角坐标系内两点,连接 ,若抛物线与线段 只有一个公共点,结合图象,直接写出 的取值范围.22. 已知,矩形 中, ,点 为 上一动点,连结 ,把 沿 折叠,使点 落在 处,当 的长是多少时, 为等腰三角形?一数学小组在解决这个问题时,发现用常规的方法不容易解决问题,于是想用函数的方法去研究,根据点 的不同位置,画出相应图形,测量线段 , , 的长度,得到下表的几组对应值.
(1)、已知 ,求抛物线的解析式及顶点 的坐标;(2)、设点 为抛物线上一点,若 ,且 的纵坐标 满足 ,求代数式 的值;(3)、已知,点 , 为平面直角坐标系内两点,连接 ,若抛物线与线段 只有一个公共点,结合图象,直接写出 的取值范围.22. 已知,矩形 中, ,点 为 上一动点,连结 ,把 沿 折叠,使点 落在 处,当 的长是多少时, 为等腰三角形?一数学小组在解决这个问题时,发现用常规的方法不容易解决问题,于是想用函数的方法去研究,根据点 的不同位置,画出相应图形,测量线段 , , 的长度,得到下表的几组对应值.0
1
2
3
4
5
6
7
7
6
5
4
2
0
7
5.2
4.6
5.0
5.6
6.2
6.7
7
(1)、填空:上表中 , .(2)、操作中发现:
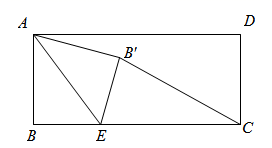
当点 为 的中点时, 为等腰三角形,请简要说明理由.(3)、将线段 的长度作为自变量 , , 的长度都是 的函数,记做 , .其中 的图象如图所示,请在同一坐标系中画出函数 的图象. (4)、结合函数图象直接写出,当线段 的长度为多少时, 为等腰三角形(精确到 ).23. 如图①,在 中, , ,点 , 分别为边 , 上的点,且 ,连接 ,点 , , 分别为线段 , , 的中点,连接 , .
(4)、结合函数图象直接写出,当线段 的长度为多少时, 为等腰三角形(精确到 ).23. 如图①,在 中, , ,点 , 分别为边 , 上的点,且 ,连接 ,点 , , 分别为线段 , , 的中点,连接 , . (1)、观察猜想:如图① ; .(2)、探究证明:将图①中的 绕点 顺时针旋转到图②的位置,这时(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出新的结论.(3)、问题解决:把 绕点 在平面内自由旋转,若 , ,请直接写出线段 长的最大值和最小值.
(1)、观察猜想:如图① ; .(2)、探究证明:将图①中的 绕点 顺时针旋转到图②的位置,这时(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出新的结论.(3)、问题解决:把 绕点 在平面内自由旋转,若 , ,请直接写出线段 长的最大值和最小值.