广西南宁市宾阳县2021年数学适应性测试卷

试卷更新日期：2021-08-24 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果温度上升3℃记作 $+ 3 ℃$ ，那么温度下降5℃记作（）

A、 $+ 2 ℃$ B、 $- 2 ℃$ C、 $+ 5 ℃$ D、 $- 5 ℃$

查看试题解析
2. 如图是一个纸巾盒，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列事件中，宜采用抽样调查方式的是（）

A、调查某社区居民购物的付款方式 B、对长征五号遥三运载火箭各个零件的检查 C、调查某中学九（1）班学生上学的出行方式 D、调查某公司五个部门4月份用电量情况

查看试题解析
4. 2020年6月23日，北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空，6月30日成功定点于距离地球36002公里的地球同步轨道．将36000用科学记数法表示应为（）

A、 ${\begin{matrix} 0.36 \times 10 \end{matrix}}^{5}$ B、 $3.6 \times 10^{5}$ C、 $3.6 \times 10^{4}$ D、 $36 \times 10^{3}$

查看试题解析
5. 如图，已知 $A B // C D$ ， $∠ A B C = 115 °$ ， $∠ C D E = 35 °$ ，则 $∠ C E D$ 的度数为（）

A、80° B、75° C、70° D、65°

查看试题解析
6. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $2 a + 3 b = 6 a b$ C、 ${(- \frac{1}{2} a^{2} b)}^{3} = - \frac{1}{8} a^{6} b^{3}$ D、 $- a (3 a - 4) = - 3 a^{2} - 4 a$

查看试题解析
7. 如图，在 $▱ A B C D$ 中， $B C = 6$ ， $∠ C = 60 °$ ，观察图中尺规作图的痕迹，可知 $D H$ 的长度为（）

A、3 B、6 C、 $6 \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
8. 随着5G网络技术的发展，市场对5G产品的需求越来越大，为满足市场需求，某大型5G产品生产厂家更新技术后，加快了生产速度，现在平均每天比更新技术前多生产30万件产品，现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同，设更新技术前每天生产x万件，依据题意得（）

A、 $\frac{400}{x - 30} = \frac{500}{x}$ B、 $\frac{400}{x} = \frac{500}{x + 30}$ C、 $\frac{400}{x} = \frac{500}{x - 30}$ D、 $\frac{400}{x + 30} = \frac{500}{x}$

查看试题解析
9. 中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是，有人要去某关口，路程378里，第一天健步行走，第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，则此人第六天走的路程为（）

A、24里 B、12里 C、6里 D、3里

查看试题解析
10. 如图，是古希腊数学家希波克拉底所研究的月牙问题，此图由三个半圆构成，三个半圆的直径分别为 $R t △ A B C$ 的三条边，若 $B C = 12$ ， $∠ A C B = 30 °$ ，则阴影部分的面积为（）

A、 $18 \sqrt{3} - π$ B、 $18 \sqrt{3}$ C、 $18 \sqrt{3} + 2 π$ D、 $8 \sqrt{3} + 2 π$

查看试题解析
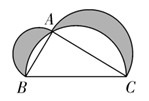11. 如图①，五象泉雕塑是南宁市的标志性城雕，位于埌东新区的金湖广场内，它以独特的方式向八方来客诉说着南宁的历史文化渊源.如图②，南南的目高 $C D$ 为1.7米，他站在 $D$ 处测得五象泉雕塑 $A B$ 的顶点 $A$ 的仰角 $∠ A C G$ 为45°，宁宁的目高 $E F$ 为1.5米，她站在 $F$ 处测得雕塑顶点 $A$ 的仰角 $∠ A E H$ 为60°，已知两人之间的距离 $D F$ 为35米，且点 $D$ 、 $B$ 、 $F$ 在同一水平线上，则该雕塑的高度 $A B$ 约为（ $\sqrt{3} \approx 1.7$ ，结果保留整数）（）

A、22米 B、23米 C、23.7米 D、24米

查看试题解析
12. 如图，四边形 $A B C D$ 内接于直径为4的 $⊙ O$ ， $A B = A C$ ， $E$ 是弦 $A C$ 和直径 $B D$ 的交点， $E D = \frac{4}{5}$ ，则弦 $A D$ 的长为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{4 \sqrt{3}}{3}$ C、 $2 \sqrt{3}$ D、 $\sqrt{6}$

查看试题解析

二、填空题

13. 当 $x =$ 时，分式 $\frac{x - 3}{2 x + 3}$ 的值为零.

查看试题解析
14. 分解因式： $2 a^{2} - 2 b^{2}$ ．

查看试题解析
15. 某摄影爱好者打算周末游玩南宁，为了体验如长廊画卷般的邕江滨水，现从熟知的3座大桥：邕江大桥、中兴大桥、白沙大桥中随机选两座桥摄影，则恰好选到邕江大桥的概率为.

查看试题解析
16. 如图，已知二次函数 $y_{1} = x^{2} - 3 x$ 的图象与正比例函数 $y_{2} = x$ 的图象在第一象限交于点 $A$ ，与 $x$ 轴正半轴交于点 $B$ ，若 $y_{1} < y_{2}$ ，则 $x$ 的取值范围是.

查看试题解析
17. 如图，矩形 $O A B C$ 的边 $O A$ 、 $O C$ 在坐标轴上，点 $B$ 在第一象限，且在反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象上，若正方形 $O A F G$ 的面积为 $S_{1}$ ，正方形 $O C D E$ 的面积为 $S_{2}$ ，若 $S_{1} + S_{2} = 35$ ，矩形 $O A B C$ 的周长为14，则 $k$ 的值为.

查看试题解析
18. 一组正方形按如图所示的方式放置，其中顶点 $B_{1}$ 在 $y$ 轴上，顶点 $C_{1}$ ， $E_{1}$ ， $E_{2}$ ， $C_{2}$ ， $E_{3}$ ， $E_{4}$ ， $C_{3}$ ……在 $x$ 轴上，已知正方形 $A_{1} B_{1} C_{1} D_{1}$ 的边长为1， $∠ B_{1} C_{1} O = 60 °$ ， $B_{1} C_{1} // B_{2} C_{2} // B_{3} C_{3}$ ……则正方形 $A_{2021} B_{2021} C_{2021} D_{2021}$ 的边长是.

查看试题解析

三、解答题

19. 计算： $- 1^{2021} + {(π - 3)}^{0} - | - 3 | \times \frac{\sqrt{2}}{4} \times \sqrt{2}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} x - 1 \geq 1 \\ \frac{2 x + 1}{3} < x - 1 \end{array}$ ，并把解集在数轴上表示出来.

查看试题解析
21. 为了让学生掌握知识更加牢固，某校九年级物理组老师们将物理实验的教学方式由之前的理论教学改进为理论 $+$ 实践，一段时间后，从九年级随机抽取15名学生，对他们在教学方式改进前后的物理实验成绩（百分制）进行整理、描述和分析（成绩用 $x$ 表示，共分成4组：A. $60 \leq x < 70$ ，B. $70 \leq x < 80$ ，C. $80 \leq x < 90$ ，D. $90 \leq x \leq 100$ ），下面给出部分信息：
教学方式改进前抽取的学生的成绩在C组中的数据为：80，83，85，87，89

教学方式改进后抽取的学生成绩为：70，72，76，82，84，86，86，93，95，90，100，98，88，100，100

教学方式改进前后抽取的学生成绩对比统计表

统计量

改进前

改进后

平均数

88

88

中位数

$a$

$b$

众数

98

$c$

根据以上信息，解答下列问题：

(1)、直接写出上述表 $a$ 、 $b$ 、 $c$ 的值；

(2)、根据以上数据，你认为该校九年级学生的物理实验成绩在教学方式改进前好，还是改进后好？请说明理由.（至少写2条理由）；

(3)、若该校九年级有300名学生，规定物理实验成绩在90分及以上为优秀，估计教学方式改进后成绩为优秀的学生人数是多少？

查看试题解析
22. 如图，在平面直角坐标系中，已知 $△ A B C$ 的三个顶点分别是A(−1，4)，B(−3，2)，C(−2，1).

（ 1 ）请画出 $△ A B C$ 关于原点 $O$ 的中心对称图形 $△ A_{1} B_{1} C_{1}$ ；

（ 2 ）请画出将 $△ A B C$ 绕点 $C$ 逆时针旋转90°后得到的 $△ A_{2} B_{2} C$ ；

（ 3 ）在（2）的条件下，求点 $A$ 旋转到点 $A_{2}$ 所经过的路线长（结果保留 $π$ ）.

查看试题解析
23. 如图，在正方形 $A B C D$ 中， $E$ ， $F$ 分别在边 $A B$ ， $B C$ 上， $△ D E F$ 是等边三角形，连接 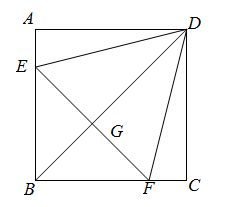$B D$ 交 $E F$ 于点 $G$ .

(1)、求证： $B E = B F$ ；

(2)、若 $D E = 2$ ，求 $B D$ 的长.

查看试题解析
24. 受疫情的影响，很多农产品滞销，各大电商发起了“爱心助农”活动，帮助农户进行农产品销售.已知某种橘子的成本为4元/千克，经过市场调查发现，一天内橘子的销售量y(千克)与销售单价x(元/千克)(4≤x≤10)的函数关系如下图所示：

(1)、当4≤x≤8时，求y与x的函数解析式；

(2)、当4≤x≤8时，要使一天内获得的利润为1200元，单价应定为多少？

(3)、求橘子的单价定为多少时，一天内获得的利润最大，最大利润为多少？

查看试题解析
25. 如图， $⊙ O$ 的直径 $A B = 10 ，$ 弦 $A C = 6 ， ∠ A C B$ 的平分线交 $⊙ O$ 于 $D ，$ 过点 $D$ 作 $D E ∥ A B$ 交 $C A$ 延长线于点 $E$ ，连接 $A D ， B D .$

(1)、由 $A B$ ， $B D$ ， $\overset{⌢}{A D}$ 围成的曲边三角形的面积是；

(2)、求证： $D E$ 是 $⊙ O$ 的切线；

(3)、求线段 $D E$ 的长.

查看试题解析
26. 如图1，抛物线 $y = a x^{2} + 2 x + c (a \neq 0)$ 与 $x$ 轴， $y$ 轴分别交于点 $A (- 1 ， 0)$ ， $B$ 点， $C (0 ， 3)$ 三点.

(1)、求抛物线的解析式；

(2)、点 $D (m ， 3)$ 在抛物线上，连接 $B C$ ， $B D$ .在对称轴左侧的抛物线上是否存在一点 $P$ ，满足 $∠ P B C = ∠ D B C$ ？如果存在，请求出点 $P$ 点的坐标；如果不存在，请说明理由；

(3)、点 $N$ 在抛物线的对称轴上，点 $M$ 在抛物线上，当以 $M$ 、 $N$ 、 $B$ 、 $C$ 为顶点的四边形是平行四边形时，请直接写出点 $M$ 的坐标.

查看试题解析

统计量	改进前	改进后
平均数	88	88
中位数	$a$	$b$
众数	98	$c$