广西河池市凤山县2021年数学初中学业水平模拟试卷(二)
试卷更新日期:2021-08-24 类型:中考模拟
一、单选题
-
1. 下列各数中,比-2大的数是( )A、-1 B、-2.5 C、-3 D、-3.52. 如图,若 ,则 的度数为( )
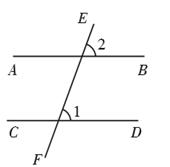 A、 B、 C、 D、3. 下列调查中,适宜采用全面调查的是( ).A、调查某池墙中现有鱼的数量 B、调查某批次汽车的抗撞击能力 C、选出某班短跑最快的学生参加全校短跑比赛 D、调查市场上某种食品的色素含量是否符合国家标准4. 下列几何体中的俯视图是三角形的是( )A、
A、 B、 C、 D、3. 下列调查中,适宜采用全面调查的是( ).A、调查某池墙中现有鱼的数量 B、调查某批次汽车的抗撞击能力 C、选出某班短跑最快的学生参加全校短跑比赛 D、调查市场上某种食品的色素含量是否符合国家标准4. 下列几何体中的俯视图是三角形的是( )A、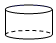 B、
B、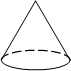 C、
C、 D、
D、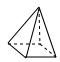 5. 若6(y+2)=30,则y的值是( )A、6 B、3 C、2 D、16. 因式分解 ( )A、 B、 C、 D、7. 下列计算中正确的是( )A、 B、 C、 D、8. 一次函数 的图象不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )A、
5. 若6(y+2)=30,则y的值是( )A、6 B、3 C、2 D、16. 因式分解 ( )A、 B、 C、 D、7. 下列计算中正确的是( )A、 B、 C、 D、8. 一次函数 的图象不经过( ).A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知点P(m﹣3,m﹣1)在第二象限,则m的取值范围在数轴上表示正确的是( )A、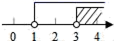 B、
B、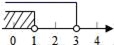 C、
C、 D、
D、 10. 如图, 内接于 ,若 , 的半径 ,则阴影部分的面积为( )
10. 如图, 内接于 ,若 , 的半径 ,则阴影部分的面积为( )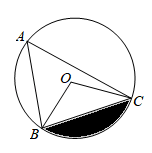 A、 B、 C、 D、11. 如图,在长为100 m,宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2 , 则道路的宽应为多少米?设道路的宽为x m,则可列方程为 ( )
A、 B、 C、 D、11. 如图,在长为100 m,宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644m2 , 则道路的宽应为多少米?设道路的宽为x m,则可列方程为 ( )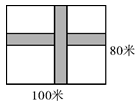 A、100×80-100x-80x=7644 B、(100-x)(80-x)+x2=7644 C、(100-x)(80-x)=7644 D、100x+80x-x2=764412. 如图,菱形OABC的顶点O(0,0),A(﹣2,0),∠B=60°,若菱形绕点O顺时针旋转90°后得到菱形OA1B1C1 , 依此方式,绕点O连续旋转2020次得到菱形OA2020B2020C2020 , 那么点C2020的坐标是( )
A、100×80-100x-80x=7644 B、(100-x)(80-x)+x2=7644 C、(100-x)(80-x)=7644 D、100x+80x-x2=764412. 如图,菱形OABC的顶点O(0,0),A(﹣2,0),∠B=60°,若菱形绕点O顺时针旋转90°后得到菱形OA1B1C1 , 依此方式,绕点O连续旋转2020次得到菱形OA2020B2020C2020 , 那么点C2020的坐标是( )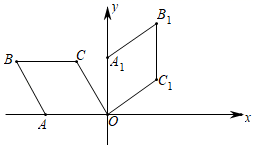 A、( ,1) B、(1,﹣ ) C、(﹣ ,﹣1) D、(﹣1, )
A、( ,1) B、(1,﹣ ) C、(﹣ ,﹣1) D、(﹣1, )二、填空题
-
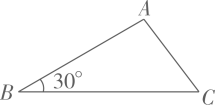
13. 的倒数是.14. 化简 的结果是.15. 如图,在△ 中, , , .则 边的长为.
 16. 如图,△ABC≌△DEC,∠ACD=28°,则∠BCE=°.
16. 如图,△ABC≌△DEC,∠ACD=28°,则∠BCE=°.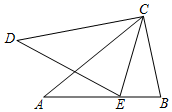 17. 如图, 是反比例函数 图象上的一点,过点 向 轴作垂线交于点 ,连接 .若图中阴影部分的面积是1,则此反比例函数的解析式为.
17. 如图, 是反比例函数 图象上的一点,过点 向 轴作垂线交于点 ,连接 .若图中阴影部分的面积是1,则此反比例函数的解析式为.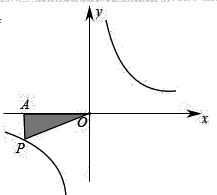 18. 如图所示,将一个半径 ,圆心角 的扇形纸板放置在水平面的一条射线 上.在没有滑动的情况下,将扇形 沿射线 翻滚至 再次回到 上时,则半径 的中点P运动的路线长为 .
18. 如图所示,将一个半径 ,圆心角 的扇形纸板放置在水平面的一条射线 上.在没有滑动的情况下,将扇形 沿射线 翻滚至 再次回到 上时,则半径 的中点P运动的路线长为 .
三、解答题
-
19. 计算:20. 解方程: .21. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
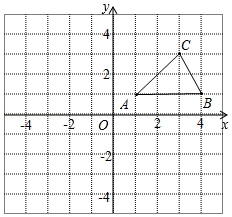
( 1 )将△ABC向下平移5个单位后得到△A1B1C1 , 请画出△A1B1C1;
( 2 )将△ABC绕原点O逆时针旋转90°后得到△A2B2C2 , 请画出△A2B2C2;
( 3 )判断以O,A1 , B为顶点的三角形的形状.(无须说明理由)
22. 甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如图所示的尚不完整的统计图表.甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
8
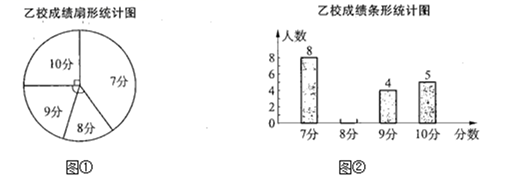 (1)、在图①中,“7分”所在扇形的圆心角等于 ;(2)、请你将②的统计图补充完整;(3)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好;(4)、如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?23. 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB
(1)、在图①中,“7分”所在扇形的圆心角等于 ;(2)、请你将②的统计图补充完整;(3)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好;(4)、如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?23. 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB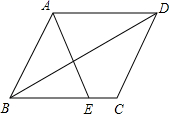 (1)、求证:∠ABE=∠EAD;(2)、若∠AEB=2∠ADB,求证:四边形ABCD是菱形.24. 我市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.(1)、A、B两种奖品每件各多少元?(2)、现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?25. 如图,以AB为直径的 经过 的顶点C,过点O作 交 于点D,交AC于点F,连接BD交AC于点G,连接CD,在OD的延长线上取一点E,连接CE,使 .
(1)、求证:∠ABE=∠EAD;(2)、若∠AEB=2∠ADB,求证:四边形ABCD是菱形.24. 我市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.(1)、A、B两种奖品每件各多少元?(2)、现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?25. 如图,以AB为直径的 经过 的顶点C,过点O作 交 于点D,交AC于点F,连接BD交AC于点G,连接CD,在OD的延长线上取一点E,连接CE,使 .
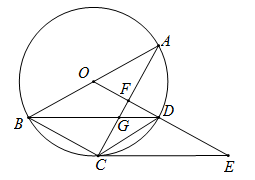 (1)、求证:EC是 的切线(2)、若 的半径是3, ,求CE的长.26. 抛物线 与 轴交于 , 两点,与 轴交于点 ,已知点 的坐标为 ,点 的坐标为 .
(1)、求证:EC是 的切线(2)、若 的半径是3, ,求CE的长.26. 抛物线 与 轴交于 , 两点,与 轴交于点 ,已知点 的坐标为 ,点 的坐标为 .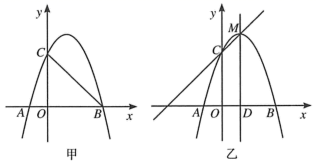 (1)、求抛物线的解析式.(2)、如图甲,若 为 上方抛物线上的一个动点,当 的面积最大时,求点 的坐标.(3)、如图乙, 为该抛物线的顶点,直线 轴于点 ,在直线 上是否存在点 ,使点 到直线 的距离等于点 到点 的距离?若存在,求出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式.(2)、如图甲,若 为 上方抛物线上的一个动点,当 的面积最大时,求点 的坐标.(3)、如图乙, 为该抛物线的顶点,直线 轴于点 ,在直线 上是否存在点 ,使点 到直线 的距离等于点 到点 的距离?若存在,求出点 的坐标;若不存在,请说明理由.