广西崇左市江州区2021年数学中考模拟试卷(三)
试卷更新日期:2021-08-24 类型:中考模拟
一、单选题
-
1. 下列四个实数中,最小的数是( )A、-3 B、-2 C、0 D、2. 下列事件属于不可能事件的是( )A、乘公交车到十字路口,遇到红灯 B、水在一个标准大气压下,温度为-1℃时结冰 C、任选13个人,至少有2个人的出生月份相同 D、在全是白球的袋子中任意摸出1个球,结果是黑色3. 如图,已知∠1=∠2,∠3=30°,则∠B的度数是( )
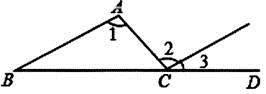 A、 B、 C、 D、4. “厉行勤俭节约,反对铺张浪费”势在必行,2020年最新统计数据显示,中国每年浪费食物总量折合为粮食大约是2.1亿人一年的口粮,将2.1亿用科学记数法表示为( )A、2.1×109 B、2.1×108 C、0.21×1010 D、21×1085. 下列计算正确的是 ( )A、 B、 C、 D、6. 若分式 的值为0,则x的值为( )A、3 B、-3 C、±3 D、07. 如图,圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成圆形阴影.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( )
A、 B、 C、 D、4. “厉行勤俭节约,反对铺张浪费”势在必行,2020年最新统计数据显示,中国每年浪费食物总量折合为粮食大约是2.1亿人一年的口粮,将2.1亿用科学记数法表示为( )A、2.1×109 B、2.1×108 C、0.21×1010 D、21×1085. 下列计算正确的是 ( )A、 B、 C、 D、6. 若分式 的值为0,则x的值为( )A、3 B、-3 C、±3 D、07. 如图,圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成圆形阴影.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为( ) A、0.36πm2 B、0.81πm2 C、1.44πm2 D、3.24πm28. 如图,在△ABC中,AB=AC,AE=2,BE=1,观察尺规作图的痕迹,则 的长度是( )
A、0.36πm2 B、0.81πm2 C、1.44πm2 D、3.24πm28. 如图,在△ABC中,AB=AC,AE=2,BE=1,观察尺规作图的痕迹,则 的长度是( ) A、2 B、3 C、 D、9. 在一块宽为20 m,长为32 m的矩形空地上修建花坛,如果在四周留出同样宽的小路,余下的部分修建花坛,使花坛的面积为540 m2 , 求小路的宽.设小路宽为x m,根据题意,所列方程正确的是 ( )A、(20-x)(32-x)=540 B、(20-x)(32-x)=100 C、(20-2x)(32-2x )=540 D、(20-2x)(32-2x)=10010. 如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3 , 若S1=3,S3=9,则S2的值为( )
A、2 B、3 C、 D、9. 在一块宽为20 m,长为32 m的矩形空地上修建花坛,如果在四周留出同样宽的小路,余下的部分修建花坛,使花坛的面积为540 m2 , 求小路的宽.设小路宽为x m,根据题意,所列方程正确的是 ( )A、(20-x)(32-x)=540 B、(20-x)(32-x)=100 C、(20-2x)(32-2x )=540 D、(20-2x)(32-2x)=10010. 如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3 , 若S1=3,S3=9,则S2的值为( )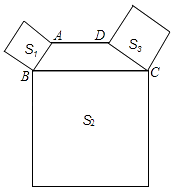 A、12 B、18 C、24 D、4811. 如图,菱形 在第一象限内, ,反比例函数 的图象经过点 ,交 边于点 ,若 的面积为 ,则 的值为( )
A、12 B、18 C、24 D、4811. 如图,菱形 在第一象限内, ,反比例函数 的图象经过点 ,交 边于点 ,若 的面积为 ,则 的值为( ) A、 B、 C、 D、412. 如图①,点P为矩形ABCD边上一个动点,运动路线是A→B→C→D→A,设点P运动的路径长为x,S△ABP=y,图②是y随x变化的函数图象,则矩形对角线AC的长是( )
A、 B、 C、 D、412. 如图①,点P为矩形ABCD边上一个动点,运动路线是A→B→C→D→A,设点P运动的路径长为x,S△ABP=y,图②是y随x变化的函数图象,则矩形对角线AC的长是( ) A、2 B、6 C、12 D、24
A、2 B、6 C、12 D、24二、填空题
-
13. 计算:2-(-3)= ;14. 若一次函数y=(m-1)x+3的函数值y随x的增大而减小,则m的取值范围是;15. 已知关于x的一元二次方程2x2-kx+4=0有两个相等的实数根,则k的值为;16. 一船向东航行,上午9:00到达一座灯塔P的西南68 n mine的M处,上午11:00到达这座灯塔的正南的N处,则船的航行速度为(结果保留根号);
 17. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为
17. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为 18. 如图,若从一块半径是6cm的圆形纸片圆O上剪出一个圆心角为60°的扇形(点A、B、C在圆O上),再将剪下的扇形围成一个圆锥,则该圆锥的底面圆半径是cm.
18. 如图,若从一块半径是6cm的圆形纸片圆O上剪出一个圆心角为60°的扇形(点A、B、C在圆O上),再将剪下的扇形围成一个圆锥,则该圆锥的底面圆半径是cm.
三、解答题
-
19. 计算: .20. 解方程: .21. 如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4).

( 1 )请在图中,画出△ABC向左平移6个单位长度后得到的△A1B1C1;
( 2 )以点O为位似中心,将△ABC缩小为原来的 ,得到△A2B2C2 , 请在图中y轴右侧,画出△A2B2C2 , 并求出∠A2C2B2的正弦值.
22. 2021年2月10日“天问一号”火星探测器抵达火星轨道,成为中国首颗人造火星卫星.某校组织首届“航天梦报国情”航天知识竞赛活动,八年级全体学生参加了“航天知识竞赛”,为了解本次竞赛的成绩,小军随机抽取八年级20名参赛学生的成绩,收集数据(单位:分)如下:90,75,80,80,70,75,80,85,82,95,
95,75,90,70,92,95,84,75,85,67
整理数据:
成绩x/分
60≤x<70
70≤x<80
80≤x<90
90≤x<100
频数
1
6
a
b
分析数据:
平均数
中位数
众数
82
c
d
根据上述数据回答以下问题:
(1)、请直接写出表格中a,b,c,d的的值.(2)、活动组委会决定,给“航天知识竞赛”成绩在90分及以上的同学授予“小宇航员”称号.根据上面的统计结果,估计该校八年级550人中约有多少人将获得“小宇航员”称号.(3)、本次活动中获得“小宇航员”称号的小红得到了A,B,C,D四枚纪念章(除图案外完全相同).她将这四枚纪念章背面朝上放在桌面上,从中随机选取两枚送给小军,请画树状图或列表求小红送给小军的两枚纪念章中恰好有一枚是B的概率.23. 如图,在等边△ABC中,D是BC的中点,以AD为边向左侧作等边△ADE,边ED与AB交于点G. (1)、求∠CAE 的度数;(2)、取AB的中点F,连接CF,EF,求证:四边形CDEF是平行四边形.24. 某电器超市销售每台进价分别200元,170元的 , 两种型号的电风扇,下表是近两周的销售情况:
(1)、求∠CAE 的度数;(2)、取AB的中点F,连接CF,EF,求证:四边形CDEF是平行四边形.24. 某电器超市销售每台进价分别200元,170元的 , 两种型号的电风扇,下表是近两周的销售情况:销售时段
销售数量
销售收入
种型号
种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)、求 , 两种型号的电风扇的销售单价;(2)、若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求 种型号的电风扇最多能采购多少台;(3)、在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.25. 在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,⊙O的切线BP与AC的延长线交于点P,连接DE,BE. (1)、求证:BD=DE;(2)、∠AED=∠BCP;(3)、已知:sin∠BAD= ,AB=10,求AP的长.26. 如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)、求证:BD=DE;(2)、∠AED=∠BCP;(3)、已知:sin∠BAD= ,AB=10,求AP的长.26. 如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.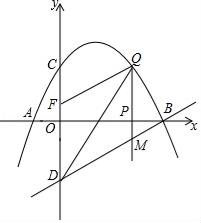 (1)、求该抛物线所表示的二次函数的表达式;(2)、已知点F(0, ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?(3)、点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求该抛物线所表示的二次函数的表达式;(2)、已知点F(0, ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?(3)、点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.