2021-2022学年人教版八年级上册数学期中质量检测卷
试卷更新日期:2021-08-24 类型:期中考试
一、单选题
-
1. 下列四个图案中,不是轴对称图形是( )A、
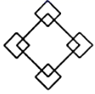 B、
B、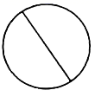 C、
C、 D、
D、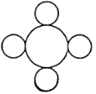 2. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、83. 到三角形的三个顶点距离相等的点是( )A、三条角平分线的交点 B、三条边的垂直平分线的交点 C、三条高的交点 D、三条中线的交点4. 用直尺和圆规作一个角等于已知角的示意图如图,则说明 ,两个三角形全等的依据是( )
2. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、83. 到三角形的三个顶点距离相等的点是( )A、三条角平分线的交点 B、三条边的垂直平分线的交点 C、三条高的交点 D、三条中线的交点4. 用直尺和圆规作一个角等于已知角的示意图如图,则说明 ,两个三角形全等的依据是( )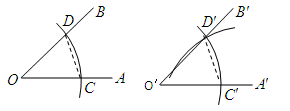 A、 B、 C、 D、不能确定5. 一个正多边形的一个内角是它相邻的外角的3倍,则这个正多边形的边数是( )A、12 B、10 C、8 D、66. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )
A、 B、 C、 D、不能确定5. 一个正多边形的一个内角是它相邻的外角的3倍,则这个正多边形的边数是( )A、12 B、10 C、8 D、66. “三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动、C点固定,OC=CD=DE,点D、E可在槽中滑动.若∠BDE=75°,则∠CDE的度数是( )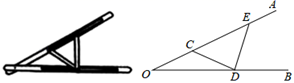 A、90° B、80° C、70° D、60°7. 若点 关于原点对称的点是点B,点B关于x轴对称的点是点C,则点C的坐标是( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,DE是AC边的中垂线,分别交AC,AB于点E,D,则△DBC的周长为( )
A、90° B、80° C、70° D、60°7. 若点 关于原点对称的点是点B,点B关于x轴对称的点是点C,则点C的坐标是( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,DE是AC边的中垂线,分别交AC,AB于点E,D,则△DBC的周长为( )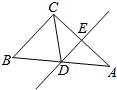 A、6 B、7 C、8 D、99. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A、6 B、7 C、8 D、99. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
 A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)10. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( )
A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)10. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( ) A、19.2° B、8° C、6° D、3°
A、19.2° B、8° C、6° D、3°二、填空题
-
11. 下列图形:①角;②直角三角形;③等边三角形;④线段;⑤等腰三角形;⑥平行四边形.其中一定是轴对称图形的有个.
12. 如图,点A、B、C、D在同一直线上,∠AEC=∠DFB,AB=DC,请补充一个条件:能使用“ ”的方法得△ACE≌△DBF.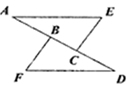 13. 如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为.
13. 如图,△ABC中,∠A=60°,∠B=50°,D、E分别是AB、AC上两点,连接DE并延长,交BC的延长线于点F,此时,∠F=35°,则∠1的度数为.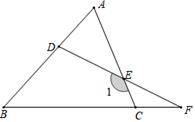 14. 在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A=度.
14. 在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A=度.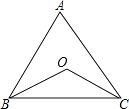 15. 已知△ABC≌△DEF,△ABC的三边分别为3,m,n,△DEF的三边分别为5,p,q.若△ABC的三边均为整数,则m+n+p+q的最大值为.16. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种.
15. 已知△ABC≌△DEF,△ABC的三边分别为3,m,n,△DEF的三边分别为5,p,q.若△ABC的三边均为整数,则m+n+p+q的最大值为.16. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种. 17. 如图,正八边形和正五边形按如图方式拼接在一起,则∠ABC的度数为。
17. 如图,正八边形和正五边形按如图方式拼接在一起,则∠ABC的度数为。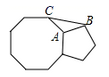 18. 如图,△ABC的三边AB、BC、CA的长分别为30、40、15,点P是三条角平分线的交点,将△ABC分成三个三角形,则 ︰ ︰ 等于
18. 如图,△ABC的三边AB、BC、CA的长分别为30、40、15,点P是三条角平分线的交点,将△ABC分成三个三角形,则 ︰ ︰ 等于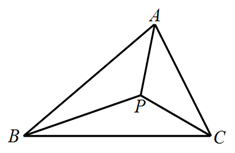
三、解答题
-
19. 如图,△ABC中,AD是BC边上的中线,E,F为直线AD上的点,连接BE,CF,且BE∥CF.求证:BE=CF.
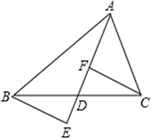 20. 已知一个多边形的每个外角都相等,且每个外角比与它相邻的内角小100°,求这个多边形的边数.21.
20. 已知一个多边形的每个外角都相等,且每个外角比与它相邻的内角小100°,求这个多边形的边数.21.已知:如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,AD=1,求∠DAB的度数.
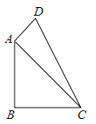 22. 如图,△ABE和△BCD都是等边三角形,且每个角是60°,那么线段AD与EC有何数量关系?请说明理由.
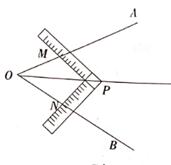
22. 如图,△ABE和△BCD都是等边三角形,且每个角是60°,那么线段AD与EC有何数量关系?请说明理由.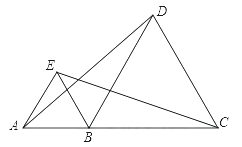 23. 在数学活动课上,李老师让同学们试着用角尺平分∠AOB(如图所示),有两组同学设计了如下方案:
23. 在数学活动课上,李老师让同学们试着用角尺平分∠AOB(如图所示),有两组同学设计了如下方案:方案①将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度位于OA,OB上,且交点分别为M,N,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线。
方案②:在边OA,OB上分别截取OM=ON,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与点M,N重合,即PM=PN,过角尺顶点P的射线OP就是∠AOB的平分线。
请分别说明方案①与方案②是否可行?若可行,请证明;若不可行,请说明理由。
 24. 已知在平面直角坐标系中有三点A(﹣2,1),B(3,1),C(2,3),请解答下列问题:
24. 已知在平面直角坐标系中有三点A(﹣2,1),B(3,1),C(2,3),请解答下列问题: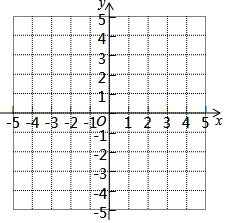 (1)、在坐标系内描出A,B,C的位置;(2)、画出△ABC关于x轴对称的图形△A1B1C1 , 并写出顶点A1 , B1 , C1的坐标;(3)、写出∠C的度数.25. 如图,△ABC 中,AD⊥BC,EF 垂直平分 AC,交 AC 于点 F,交 BC 于点 E,且 BD=DE.
(1)、在坐标系内描出A,B,C的位置;(2)、画出△ABC关于x轴对称的图形△A1B1C1 , 并写出顶点A1 , B1 , C1的坐标;(3)、写出∠C的度数.25. 如图,△ABC 中,AD⊥BC,EF 垂直平分 AC,交 AC 于点 F,交 BC 于点 E,且 BD=DE.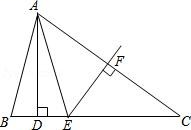 (1)、若∠BAE=40°,求∠C 的度数;(2)、若△ABC 周长 13cm,AC=6cm,求 DC 长.26. 如图①,点P、Q 分别是等边△ABC边AB、BC上的动点(端点除外),点 P从顶点 A、点Q从顶点B 同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)、若∠BAE=40°,求∠C 的度数;(2)、若△ABC 周长 13cm,AC=6cm,求 DC 长.26. 如图①,点P、Q 分别是等边△ABC边AB、BC上的动点(端点除外),点 P从顶点 A、点Q从顶点B 同时出发,且它们的运动速度相同,连接AQ、CP交于点M.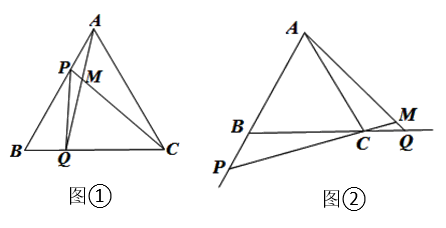 (1)、求证:△ABQ≌△CAP;(2)、当点P、Q 分别在 AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图②,若点 P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,求∠QMC的度数.
(1)、求证:△ABQ≌△CAP;(2)、当点P、Q 分别在 AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图②,若点 P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,求∠QMC的度数.