2021-2022学年人教版八年级上册数学期末质量检测卷

试卷更新日期：2021-08-23 类型：期末考试

进入出卷网下载

一、选择题

1. 下列倡导节约的图案中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算中，正确的是（）

A、 $- (m + n) = n - m$ B、 ${(m^{3} n^{2})}^{3} = m^{6} n^{5}$ C、 $m^{3} \cdot m^{2} = m^{5}$ D、 $n^{3} \div n^{3} = n$

查看试题解析
3. 若一个三角形三个内角度数的比为1:2:3，那么这个三角形是（）

A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形

查看试题解析
4. 已知：a、b、c是△ABC三边长，且M＝（a+b+c）（a+b-c）（a-b-c），那么（）

A、M＞0 B、M＝0 C、M＜0 D、不能确定

查看试题解析
5. 如果 $3 x - 4 y = 0$ ，那么代数式 $(\frac{x^{2}}{y} - y) \cdot \frac{3}{x + y}$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 已知，如图，△ABC中，AB=AC，AD是角平分线，BE=CF，则下列说法正确的有（）
（1）AD平分∠EDF；（2）△EBD≌△FCD；（3）BD=CD；（4）AD⊥BC．

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 如图，在△ABC≌△DEF，且AB＝4，BC＝6，BE=2，∠B＝60°，连接DC，则DC的长为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则下列线段的长度等于BP+EP最小值的是（）

A、BC B、AC C、AD D、CE

查看试题解析
9. 若 $\frac{| x | - 1}{x - 1}$ 的值为零，则x的值为（）

A、-1 B、1 C、 $\pm 1$ D、0

查看试题解析
10. 如图，在△ABC中，AB＝AC，AD，BE是△ABC的两条中线，P是AD上的一个动点，则下列线段的长等于CP+EP最小值的是（）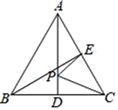

A、AC B、AD C、BE D、BC

查看试题解析

二、填空题

11. 计算： $2021^{2} - 2020^{2} =$ .

查看试题解析
12. 要使分式 $\frac{x}{x + 1}$ 有意义，则 $x$ 的取值范围是；

查看试题解析
13. 若多项式5x²+17x﹣12可因式分解成（x+a）（bx+c），其中a、b、c均为整数，则a+c之值为．

查看试题解析
14. 如图，在△ABC中，点D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A等于.

查看试题解析
15. 已知(a＋b)²＝7，(a－b)²＝4，则 ab 的值为.

查看试题解析
16. 一个多边形的内角和等于它的外角和的2倍，则这个多边形的边数是.

查看试题解析
17. 若方程 $\frac{x - 5}{x - 6} - \frac{x - 6}{x - 5} = \frac{k}{x^{2} - 11 x + 30}$ 的解不大于13，则 $k$ 的取值范围是．

查看试题解析
18. 如图，已知∠MON=30°，点A₁ ， A₂ ， A₃ ， …在射线ON上，点B₁ ， B₂ ， B₃ ， …在射线OM上，△A₁B₁A₂ ， △A₂B₂A₃ ， △A₃B₃A₄ ， …均为等边三角形，若OA₁=2，则△A₆B₆A₇的边长为.

查看试题解析

三、解答题

19. 先化简，再求值

(1)、 ${(x + 2)}^{2} - x (x + 3) + (x + 1) (x - 1)$ ，其中 $x = 2$ .

(2)、 $\frac{3 m^{2} + 9 m}{m - 2} \div (m + 2 - \frac{5}{m - 2})$ ，其中 $3 m - 12 = 0$

查看试题解析
20. 解方程： $\frac{x - 1}{x + 1} - \frac{3}{x^{2} - 1} = 1$ .

查看试题解析
21. 如图，∠AOB的内部有一点P，在射线OA，OB边上各取一点P₁ ， P₂ ，使得△PP₁P₂的周长最小，作出点P₁ ， P₂ ，叙述作图过程（作法），保留作图痕迹．

查看试题解析
22. 已知：如图，在平面直角坐标系中.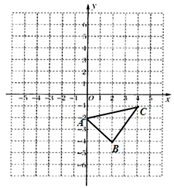

①作出△ABC关于 $y$ 轴对称的 $△ A_{1} B_{1} C_{1}$ ，并写出 $△ A_{1} B_{1} C_{1}$ 三个顶点的坐标；

②直接写出△ABC的面积为 ▲ ；

③在x轴上画点P，使PA+PC最小.

查看试题解析
23. 如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，连接EF.
求证：AD垂直平分EF.

查看试题解析
24. 2020年初武汉爆发新冠肺炎疫情，使得口罩成为人们生活的必需品，爱民药店准备购进 $N 95$ 和普通医用两种类型的口罩，已知每个普通医用口罩的进价比每个 $N 95$ 口罩的进价少8元，且用300元购进普通医用口罩的数量与用1500元购进 $N 95$ 口罩的数量相同，设每个普通医用口罩进价为 $x$ 元.

(1)、每个 $N 95$ 口罩的进价为元，1500元购进 $N 95$ 口罩的数量为个（用含 $x$ 的式子表示）；

(2)、求每个普通医用口罩、每个 $N 95$ 口罩的进价分别为多少元？

(3)、若爱民药店本次购进这两种口罩共800个，并将两种口罩均按进价加价50%全部售出利润不少于1600元（不考虑其他因素），则这次至少购进 $N 95$ 口罩多少个？

查看试题解析
25. 如图

(1)、如图①，已知：在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，直线 $m$ 经过点 $A$ ， $B D ⊥$ 直线 $m$ ， $C E ⊥$ 直线 $m$ ，垂足分别为点 $D$ 、 $E$ .求证： $D E = B D + C E$ .

(2)、如图②，将（1）中的条件改为：在 $△ A B C$ 中， $A B = A C$ ， $D$ 、 $A$ 、 $E$ 三点都在直线 $m$ 上，并且有 $∠ B D A = ∠ A E C = ∠ B A C = a$ ，其中 $a$ 为任意锐角或钝角.请问结论 $D E = B D + C E$ 是否成立？如成立，请你给出证明；若不成立，请说明理由.

(3)、拓展与应用：如图③， $D$ 、 $E$ 是 $D$ 、 $A$ 、 $E$ 三点所在直线 $m$ 上的两动点（ $D$ 、 $A$ 、 $E$ 三点互不重合），点 $F$ 为 $∠ B A C$ 平分线上的一点，且 $△ A B F$ 和 $△ A C F$ 均为等边三角形，连接 $B D$ 、 $C E$ ，若 $∠ B D A = ∠ A E C = ∠ B A C$ ，试判断 $△ D E F$ 的形状.（不需要说明理由）

查看试题解析