高中数学人教A版(2019) 选修一 第二章 直线和圆的方程
试卷更新日期:2021-08-23 类型:单元试卷
一、单选题
-
1. 若直线 的倾斜角 ,则其斜率 ( )A、 B、 C、1 D、2. 斜率为 ,在 轴上截距为 的直线方程的一般式为 ( )A、 B、 C、 D、3. 圆 截直线 所得的最短弦长为( )A、 B、 C、 D、24. 已知两直线3x+y-3=0与6x+my+1=0平行,则它们之间的距离为 ( )
A、4 B、 C、 D、5. 直线 与直线 互相垂直,则实数 的值为( )A、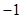 B、
B、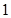 C、
C、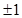 D、0
6. 圆 上的点到直线 的距离最大值是( )A、2 B、 C、 D、7. 已知P是△ABC所在平面外一点,PA,PB,PC两两垂直,且P在△ABC所在平面内的射影H在△ABC内,则H一定是△ABC的( )A、内心 B、外心 C、垂心 D、重心8. 已知圆(x﹣4)2+(y﹣4)2=4与直线y=kx的交点为P、Q,原点为O,则|OP|•|OQ|的值为( )A、2
D、0
6. 圆 上的点到直线 的距离最大值是( )A、2 B、 C、 D、7. 已知P是△ABC所在平面外一点,PA,PB,PC两两垂直,且P在△ABC所在平面内的射影H在△ABC内,则H一定是△ABC的( )A、内心 B、外心 C、垂心 D、重心8. 已知圆(x﹣4)2+(y﹣4)2=4与直线y=kx的交点为P、Q,原点为O,则|OP|•|OQ|的值为( )A、2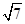 B、28
C、32
D、由k确定
B、28
C、32
D、由k确定
二、多选题
-
9. 已知 , ,记 ,则( )A、 的最小值为 B、当 最小时, C、 的最小值为 D、当 最小时10. 下列说法不正确的是( )A、 不能表示过点 且斜率为 的直线方程; B、在 轴、 轴上的截距分别为 的直线方程为 ; C、直线 与 轴的交点到原点的距离为 ; D、平面内的所有直线的方程都可以用斜截式来表示.11. 已知圆 ,直线 ,下列四个命题为真命题的是( )A、对任意实数 和 ,直线和圆相切 B、对任意实数 和 ,直线和圆有公共点 C、对任意实数 ,必存在实数 ,使得直线与圆相切 D、对任意实数 ,必存在实数 使得直线与圆相切12. 直线 与圆C: 相交于A、B两点,则AB长度可能为( )A、6 B、8 C、12 D、16
三、填空题
-
13. 经过点A(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程为14. 过点P(1,3)的直线l分别与两坐标轴交于A,B两点,若P为AB的中点,则直线l的截距式方程是.15. 已知直线 与圆心为 的圆 相交于 两点,且 ,则实数 的值为 .16. 已知圆 经过坐标原点和点 ,若直线 与圆 相切,则圆 的方程是 .
四、解答题
-
17. 已知 中, , , , ,垂足为 .
(Ⅰ)求直线 的方程;
(Ⅱ)求过点 且平行于边 的直线方程.
18. 已知直线 经过两条直线 和 的交点,且与直线 垂直.(1)、求直线 的方程;(2)、若圆 过点 ,且圆心在 轴的正半轴上,直线 被该圆所截得的弦长为 ,求圆 的标准方程.19. 已知圆 的圆心在直线 上,且经过点 和 .(1)、求圆 的标准方程;(2)、若过点 的直线 与圆 交于 , 两点,且 ,求直线 的方程.20. 已知直线l:5ax-5y-a+3=0.(1)、求证:不论a为何值,直线l总过第一象限;(2)、为了使直线l不过第二象限,求a得取值范围.