安徽省合肥市庐江县2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2021-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 早在两千多年前，中国人就已经开始使用负数，并运用到生产和生活中，比西方早一千多年，下列各式计算结果为负数的是（）

A、4+（﹣3） B、2﹣（﹣2） C、4×（﹣2） D、（﹣4）÷（﹣2）

查看试题解析
2. 2020年9月11日，巢湖水位终于回落至警戒水位10.50米，这意味着“巢湖保卫战”取得重大胜利．在这场浩大的洪水之战中，合肥市前后出动了超过155万人次抗洪．而数字155万用科学记数法表示为（）

A、1.55×10⁶ B、15.5×10⁵ C、1.55×10⁵ D、155×10⁴

查看试题解析
3. 下列说法中，正确的是（）

A、单项式 $\frac{1}{2}$ xy²的系数是 $\frac{1}{2} x$ B、单项式﹣6x²的次数为﹣6 C、多项式x³+2x+18是三次三项式 D、多项式3x²+y²﹣2的常数项是2

查看试题解析
4. 由四舍五入法得到的近似数8.16万，下列说法正确的是（）

A、精确到万位 B、精确到百位 C、精确到千分位 D、精确到百分位

查看试题解析
5. 下列计算正确的是（）

A、3a+5b＝8ab B、3a³c﹣2c³a＝a³c C、3a﹣2a＝1 D、2a^2b+3a^2b＝5a^2b

查看试题解析
6. 在 $- \frac{1}{3} ， \frac{22}{7} ， 0 ， - 3 ， 0.2 ， π ， 4 ， - 8 ， - 13$ 这些数中，有理数有 $m$ 个，整数有 $n$ 个，分数有 $k$ 个，则 $m - n + k$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
7.
如图，四个有理数在数轴上的对应点M，P，N，Q，若点M，N表示的有理数互为相反数，则图中表示绝对值最小的数的点是（　　）

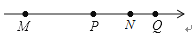A、点M B、点N C、点P D、点Q

查看试题解析
8. 如图，圆的面积为2008，五边形的面积为2021，两个图形叠放在一起，两个阴影部分的面积分别为a ， b ，则b﹣a的值为（）

A、9 B、11 C、12 D、13

查看试题解析
9. 如图是一个简单的数值运算程序，当输入n的值为时4，则输出的结果为（）

A、16 B、12 C、132 D、140

查看试题解析
10. 若x是不等于1的实数，我们把 $\frac{1}{1 - x}$ 称为x的差倒数，如3的差倒数是 $\frac{1}{1 - 3}$ ＝﹣ $\frac{1}{2}$ ，﹣ $\frac{1}{2}$ 的差倒数为 $\frac{1}{1 - (- \frac{1}{2})}$ ＝ $\frac{2}{3}$ ．现已知x₁＝2，x₂是x₁的差倒数，x₃是x₂差倒数，x₄是x₃的差倒数，…，依此类推，则x₂₀₂₀+x₂₀₂₁的和为（）

A、1 B、﹣ $\frac{1}{2}$ C、 $\frac{5}{2}$ D、﹣ $\frac{3}{2}$

查看试题解析

二、填空题

11. 如果把顺时针旋转60°记作+60°，那么逆时针旋转30°应记作．

查看试题解析
12. 定义新运算：aΩb＝﹣b+ab ，例如：（﹣4）Ω3＝﹣3+（﹣4）×3＝﹣15，那么（﹣1）Ω（﹣2）＝．

查看试题解析
13. 3a+b＝﹣1，则4（a+b）﹣8（2a+b+2）的值为．

查看试题解析
14. 数轴上有A、B两点，点A表示6的相反数，点B表示绝对值最小的数，一动点P从点B出发，沿数轴以1单位长度/秒的速度运动，4秒后，点P到点A的距离为单位长度．

查看试题解析

三、解答题

15.

(1)、（﹣2.25）+（﹣5.1）+ $\frac{1}{4}$ +（﹣4 $\frac{1}{8}$ ）+（﹣ $\frac{9}{10}$ ）；

(2)、﹣1²⁰²⁰﹣8+（﹣2）³×（﹣3）．

查看试题解析
16. 先把下列各数在数轴上表示出来，再按从小到大的顺序用“＜”号把这些数连接起来：
﹣ $\frac{1}{2}$ ，|﹣2.5|，0，﹣2² ， ﹣（﹣4）．

查看试题解析
17. 如果有理数a、b、c在数轴上的位置如图所示，试化简|a+b|+|a﹣c|﹣|b+c|．

查看试题解析
18. 先化简，再求值： $3 (x^{2} - 2 x y) - [3 x^{2} - 2 y + 2 (x y + y)]$ ，其中( $x$ ＋4)²＋∣ $y$ －2∣＝0

查看试题解析
19. 仔细观察下列等式：
第1个：5²﹣1²=8×3

第2个：9²﹣5²=8×7

第3个：13²﹣9²=8×11

第4个：17²﹣13²=8×15

…

(1)、请你写出第6个等式：；

(2)、请写出第n个等式，并加以验证；

(3)、运用上述规律，计算：8×7+8×11+…+8×399+8×403．

查看试题解析
20. 已知a、b互为相反数且 $a \neq 0$ ，c、d互为倒数，m的绝对值是最小的正整数，求 $| m | - \frac{a}{b} + \frac{2011 (a + b)}{2010} - c d$

查看试题解析
21. 庐江某出租车司机，在东西方向的周瑜大道上连续接送5批客人，行驶路程记录如下表（规定向东为正，向西为负，单位：km）：

第1批

第2批

第3批

第4批

第5批

5km

2km

﹣4km

﹣2.5km

3.5km

(1)、接送完第5批客人后，该驾驶员在起始出发地的什么方向，距离起始出发地多少千米？

(2)、若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过2.5km收费6元，超过2.5km的部分按每千米1.6元收费，在这过程中该驾驶员共收到车费多少元？

查看试题解析
22. 数学课上，张老师出示了这样一道题目：“当a $= \frac{1}{2}$ ，b＝﹣2时，求多项式7a³+3a²b+3a³+6a³b﹣3a²b﹣10a³﹣6a³b﹣1的值”解完这道题后，小阳同学指出：“a $= \frac{1}{2}$ ，b＝﹣2是多余的条件”．师生讨论后，一致认为小阳说法是正确的．

(1)、请你说明正确的理由；

(2)、受此启发，老师又出示了一道题目：“无论x，y取任何值，多项式2x²+ax﹣5y+b﹣2（bx² $- \frac{3}{2}$ x $- \frac{5}{2}$ y﹣3）的值都不变，求系数a，b的值”．请你解决这个问题．

查看试题解析
23. 某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元．“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案．
方案一：买一套西装送一条领带；

方案二：西装和领带都按定价的90%付款．

现某客户要到该商场购买西装20套，领带x条（x＞20）．

(1)、若该客户按方案一购买，需付款元．（用含x的代数式表示）若该客户按方案二购买，需付款元．（用含x的代数式表示）

(2)、若x＝30，通过计算说明此时按哪种方案购买较为合算？

(3)、当x＝30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

查看试题解析

第1批	第2批	第3批	第4批	第5批
5km	2km	﹣4km	﹣2.5km	3.5km