安徽省阜阳市太和县2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2021-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 如果60m表示“向北走60m”，那么“向南走40m”可以表示为（）

A、－20m B、－40m C、20m D、40m

查看试题解析
2. 如果 $\frac{| a |}{a}$ ＝－1，则a一定是（）

A、正数 B、负数 C、非正数 D、非负数

查看试题解析
3. 下列各组数中，相等的是（）

A、2与 $\frac{1}{2}$ 的相反数 B、 ${(- 1)}^{2}$ 与1 C、 $- 1$ 与 ${(- 1)}^{2}$ D、2与 $- | - 2 |$

查看试题解析
4. 给出下列结论：
①近似数 $8.03 \times 10^{5}$ 精确到百分位；② $- a$ 一定是个负数；③若 $| - a | = a$ ，则 $a \geq 0$ ；④∵ $a < 0$ ，∴ $- | - a | = - a$ ．其中正确的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
5. 若 $- a^{x - y + 1} b^{3}$ 与 $\frac{5}{2} a^{4} b^{y}$ 是同类项，则 $x y =$ （）

A、6 B、18 C、3 D、12

查看试题解析
6. 2018年10月24日港珠澳大桥全线通车，港珠澳大桥东起香港国际机场附近的香港口岸人工岛，向西横跨伶仃洋海域后连接珠海和澳门人工岛，止于珠海洪湾，它是世界上最长的跨海大桥，被称为“新世界七大奇迹之一”，港珠澳大桥总长度55000米，则数据55000用科学记数法表示为（）

A、55×10⁵ B、5.5×10⁴ C、0.55×10⁵ D、5.5×10⁵

查看试题解析
7. 在代数式 $\frac{5}{2} x^{2} - 3 x$ ， $2 π x^{2} y$ ， $\frac{1}{x}$ ， $- 5$ ， $a$ 中，单项式的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
8. 如图图中数轴画法错误的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 下列说法中错误的个数有（）
①1是绝对值最小的有理数；②若a²=b² ，则a³=b³；③两个四次多项式的和一定是四次多项式；④多项式x²﹣3kxy﹣3y²+ $\frac{1}{3}$ xy﹣8合并同类项后不含xy项，则k的值是 $\frac{1}{9}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 已知 $a - b = 3, c + d = 2$ 则 $(a + c) - (b - d)$ 的值是（）

A、-1 B、1 C、-5 D、5

查看试题解析

二、填空题

11. 已知 $| a | = 2 ， | b | = 3 ， | c | = 4 ，$ 且 $a > b > c ，$ 则 $a - b + c =$ .

查看试题解析
12. 如图，是一个简单的数值计算程序，当输入的x的值为5，则输出的结果为．

查看试题解析
13. 如果单项式﹣2ab^m+1与 $\frac{4}{3}$ a^n-2b³是同类项，那么（m﹣n）²⁰¹⁸＝.

查看试题解析
14. 已知等式：2+ $\frac{2}{3}$ =2²× $\frac{2}{3}$ ，3+ $\frac{3}{8}$ =3²× $\frac{3}{8}$ ，4+ $\frac{4}{15}$ =4²× $\frac{4}{15}$ ，…，10+ $\frac{a}{b}$ =10²× $\frac{a}{b}$ ，（a，b均为正整数），则a+b= ．

查看试题解析

三、解答题

15. 计算： $[{(- 1)}^{2019} - (\frac{3}{4} - \frac{1}{6} - \frac{3}{8}) \times 24] \div | - 3^{2} + 5 |$

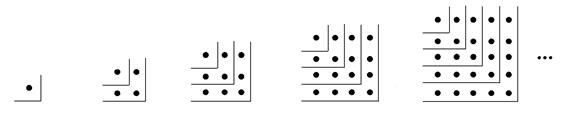
查看试题解析
16. 先化简，再求值：2（x²y+3xy）﹣3（x²y﹣1）﹣2xy﹣2，其中x＝﹣2，y＝2．

查看试题解析
17. 已知有理数a、b互为相反数，c、d互为倒数，m是最小的正整数，求代数式3(a+b)﹣(cd)⁵+m的值.

查看试题解析
18. 观察下面的点阵图和相应的等式，探究其中的规律：

(1)、在④和⑤后面的横线上分别写出相应的等式：
①1＝1²；②1＋3＝2²；③1＋3＋5＝3²；④；⑤；….

(2)、通过猜想写出与第n个点阵图相对应的等式．

查看试题解析
19. 已知A-B=7a²-7ab，且B=-4a²+6ab+7.

(1)、求A等于多少？

(2)、若|a+1|+（b-2）²=0，求A的值.

查看试题解析
20. 某中学的小卖部最近进了一批计算器，进价是每个8元，今天共卖出30个，实际卖出时以每个10元为标准，超过的记为正，不足的记为负，记录如下：

超出标准的钱数（元）

+3

﹣2

+2

+1

卖出计算器个数

7个

6个

9个

8个

(1)、这个小卖部的计算器今天卖出的平均价格是多少？

(2)、这个小卖部今天卖计算器赚了多少元？

查看试题解析
21. 如图所示：A，B，C，D四点表示的数分别为a，b，c，d，且|c|＜|b|＜|a|＜|d|.

(1)、比较大小：﹣bc，d﹣ac﹣b；

(2)、化简：|a﹣c|﹣|﹣a﹣b|+|d﹣c|.

查看试题解析
22. 老师在黑板上出了一道有理数的混合运算题 ${(- 2)}^{3} \div [- 3^{2} \times {(- \frac{2}{3})}^{2} + 2] \times \frac{1}{6}$
下面是小丽的解答过程：

(1)、小丽的解答过程共存在处错误，分别是．

(2)、请你写出正确的解答过程：

查看试题解析
23. （问题）观察下列等式
$\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4}$ ，

将以上三个等式两边分别相加得：

$\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} = 1 - \frac{1}{4} = \frac{3}{4}$ .

(1)、猜想并写出： $\frac{1}{n (n + 1)}$ =.

(2)、直接写出计算结果： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + ... + \frac{1}{2018 \times 2019} =$ .

(3)、探究并计算：
① $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + ... + \frac{1}{2015 \times 2017} + \frac{1}{2017 \times 2019}$ .

② $\frac{1}{1 \times 3} - \frac{1}{2 \times 4} + \frac{1}{3 \times 5} - \frac{1}{4 \times 6} + \frac{1}{5 \times 7} + ... + \frac{1}{17 \times 19} - \frac{1}{18 \times 20}$ .

查看试题解析

超出标准的钱数（元）	+3	﹣2	+2	+1
卖出计算器个数	7个	6个	9个	8个