辽宁省葫芦岛市连山区2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-08-23 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组长度的三条线段能组成三角形的是( )A、1,2,3 B、1,1,2 C、1,2,2 D、1,5,73. △ABC中BC边上的高作法正确的是( )A、
2. 下列各组长度的三条线段能组成三角形的是( )A、1,2,3 B、1,1,2 C、1,2,2 D、1,5,73. △ABC中BC边上的高作法正确的是( )A、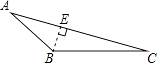 B、
B、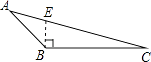 C、
C、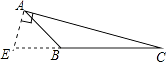 D、
D、 4. 在 中, ,那么另一个锐角 的度数是( )A、 B、 C、 D、5. 如图,CD、BD分别平分∠ACE、∠ABC , ∠A=70°,则∠BDC=( )
4. 在 中, ,那么另一个锐角 的度数是( )A、 B、 C、 D、5. 如图,CD、BD分别平分∠ACE、∠ABC , ∠A=70°,则∠BDC=( )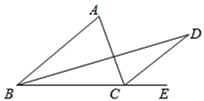 A、35° B、25° C、70° D、60°6. 如图,以正五边形 的边 为边作正方形 ,使点F , G在其内部,则 的度数是( )
A、35° B、25° C、70° D、60°6. 如图,以正五边形 的边 为边作正方形 ,使点F , G在其内部,则 的度数是( ) A、12° B、18° C、24° D、30°7. 如图,ΔAOB≌ΔCOD,A和C,B和D是对应顶点,若BO=6,AO=3,AB=5,则CD的长为( ).
A、12° B、18° C、24° D、30°7. 如图,ΔAOB≌ΔCOD,A和C,B和D是对应顶点,若BO=6,AO=3,AB=5,则CD的长为( ). A、5 B、8 C、10 D、不能确定8. 如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( )
A、5 B、8 C、10 D、不能确定8. 如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( ) A、15 B、12 C、10 D、149. 如图,在 中,分别以点A和点B为圆心,以相同的长(大于 )为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知 的面积比 的面积小4,则 的面积为( )
A、15 B、12 C、10 D、149. 如图,在 中,分别以点A和点B为圆心,以相同的长(大于 )为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.已知 的面积比 的面积小4,则 的面积为( ) A、 B、 C、 D、10. 如图,在等边 中, 于 ,延长 到 ,使 , 是 的中点,连接 并延长 交 于 , 的垂直平分线分别交 , 于点 ,点 ,连接 , ,下列结论:① ;② ;③ ;④ ;⑤ .其中正确的个数是( ).
A、 B、 C、 D、10. 如图,在等边 中, 于 ,延长 到 ,使 , 是 的中点,连接 并延长 交 于 , 的垂直平分线分别交 , 于点 ,点 ,连接 , ,下列结论:① ;② ;③ ;④ ;⑤ .其中正确的个数是( ). A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 在平面直角坐标系中,与点A(5,﹣1)关于y轴对称的点的坐标是.12. 已知一个n边形的内角和等于1980°,则n= .13. 如图,已知 , 、 相交于点F , 则 的度数是度.
 14. 如图,在ΔABC中,E、F分别是AB、AC上的两点,∠1+∠2=235°,则∠A=度.
14. 如图,在ΔABC中,E、F分别是AB、AC上的两点,∠1+∠2=235°,则∠A=度. 15. 如图所示, 内一点P, , 分别是P关于OA,OB的对称点, 交OA于点M,交OB于点N,若 ,则 的周长是.
15. 如图所示, 内一点P, , 分别是P关于OA,OB的对称点, 交OA于点M,交OB于点N,若 ,则 的周长是. 16. 如图,已知在 中, ,点 是 中点, 于点 , 于点 , ,则 的长是 .
16. 如图,已知在 中, ,点 是 中点, 于点 , 于点 , ,则 的长是 . 17. 如图,已知在 中, , 平分 ,且 , ,则 °.
17. 如图,已知在 中, , 平分 ,且 , ,则 °. 18. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到 的位置,点B , O(分别落在点 , 处,点 在x轴上,再将 绕点 顺时针旋转到 的位置,点 在x轴上,再将 绕点 顺时针旋转到 的位置,点 在x轴上,依次进行下去,…,若点A(3,0),B(0,4),AB=5,则点 的坐标为 .
18. 如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到 的位置,点B , O(分别落在点 , 处,点 在x轴上,再将 绕点 顺时针旋转到 的位置,点 在x轴上,再将 绕点 顺时针旋转到 的位置,点 在x轴上,依次进行下去,…,若点A(3,0),B(0,4),AB=5,则点 的坐标为 .
三、解答题
-
19. 在正方形网格中,建立如图所示的平面直角坐标系, 的三个顶点都在格点上, 关于y轴对称图形为 .(要求:A与 ,B与 ,C与 相对应)
 (1)、写出 的坐标,并画出 的图形;(2)、求 的面积.20. 如图,在 中, , .
(1)、写出 的坐标,并画出 的图形;(2)、求 的面积.20. 如图,在 中, , . (1)、求 的度数;(2)、 平分 交 于E , 于D , 求 的度数.21. 如图所示 ,点 在 上且 .
(1)、求 的度数;(2)、 平分 交 于E , 于D , 求 的度数.21. 如图所示 ,点 在 上且 . (1)、求证: ;(2)、若 平分 ,则 与线段 有什么关系?为什么?22. 如图,△ABC中,D为BC上一点,∠C=∠BAD , △ABC的角平分线BE交AD于点F .
(1)、求证: ;(2)、若 平分 ,则 与线段 有什么关系?为什么?22. 如图,△ABC中,D为BC上一点,∠C=∠BAD , △ABC的角平分线BE交AD于点F . (1)、求证:∠AEF=∠AFE;(2)、G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.23. 如图,已知 、 的平分线相交于点 , 过点 且 .
(1)、求证:∠AEF=∠AFE;(2)、G为BC上一点,当FE平分∠AFG且∠C=30°时,求∠CGF的度数.23. 如图,已知 、 的平分线相交于点 , 过点 且 . (1)、若 , ,求 的度数;(2)、若 , ,求 、 的度数.24. 如图, 中, , , 、 分别为 、 的垂直平分线,E、G分别为垂足.
(1)、若 , ,求 的度数;(2)、若 , ,求 、 的度数.24. 如图, 中, , , 、 分别为 、 的垂直平分线,E、G分别为垂足. (1)、求 的度数;(2)、若 的周长为20,求 的长.
(1)、求 的度数;(2)、若 的周长为20,求 的长.


