辽宁省锦州市凌海市2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 在实数：① $- \frac{1}{7} π$ ② $1.414$ ③ $0. \overset{• •}{57}$ ④ $2+ \sqrt{3}$ ⑤ $π$ ⑥ $\sqrt{9}$ 中，是无理数的为（）

A、①②③④⑤⑥ B、①③④⑤⑥ C、①③④⑥ D、①④⑤

查看试题解析
2. 若 $\sqrt{a}$ 和 $\sqrt{- a}$ 都有意义，则 $a$ 的值是（）

A、 $a \geq 0$ B、 $a \leq 0$ C、 $a = 0$ D、 $a \neq 0$

查看试题解析
3. 如图，在Rt△ABC中，∠C＝90°，D为AC上一点，且DA＝DB＝5，又△DAB的面积为10，那么DC的长是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 如图所示的象棋棋盘上，若“帅”位于点 $(1 ， - 2)$ 上，“相”位于点 $(3 ， - 2)$ 上，则“炮”位于点（）

A、 $(- 2 ， 1)$ B、 $(- 1 ， 1)$ C、 $(- 2 ， 0)$ D、 $(- 2 ， - 2)$

查看试题解析
5. （- $\sqrt{9}$ ）²的平方根是x，64的立方根是y，则x+y的值为（）

A、3 B、7 C、3或7 D、1或7

查看试题解析
6. 下列说法错误的是（）

A、若 $x + y = 0$ ，则点 $P (x ， y)$ 一定在第二、第四象限角平分线上 B、点 $P (- 2 ， 3)$ 到 $y$ 轴的距离为 $2$ C、若 $P (x ， y)$ 中 $x y = 0$ ，则 $P$ 点在 $x$ 轴上 D、点 $A (- a^{2} - 1 ， | b |)$ 可能在第二象限

查看试题解析
7. 如图，在数轴上表示 $1 ， \sqrt{3}$ 的对应点分别为 $A 、 B$ ，点 $B$ 关于点 $A$ 的对称点为 $C$ ，则点 $C$ 表示的数为（）

A、 $\sqrt{3} - 1$ B、 $1 - \sqrt{3}$ C、 $2 - \sqrt{3}$ D、 $\sqrt{3} - 2$

查看试题解析
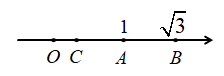8. 给出下列说法：
①在直角三角形 $A B C$ 中，已知两边长为 $3$ 和 $4$ ，则第三边长为 $5$ ；②三角形的三边 $a 、 b 、 c$ 满足 $a^{2} + b^{2} = c^{2}$ ，则 $∠ C = 90^{°}$ ；③ $Δ A B C$ 中，若 $∠ A ： ∠ B ： ∠ C = 1 ： 5 ： 6$ ，则 $Δ A B C$ 是直角三角形；④ $Δ A B C$ 中，若 $a ： b ： c = 1 ： 2 ： \sqrt{3}$ ，则这个三角形是直角三角形．

其中，错误的说法的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 数轴上，点 $A$ 表示 $\sqrt{2} + 1$ ，点 $B$ 表示 $3 - \sqrt{2}$ ，则 $A B$ 间的距离

查看试题解析
10. 比较大小： $\frac{\sqrt{3} - 1}{2}$ $\frac{1}{2}$

查看试题解析
11. 如图， $Δ A B C$ 与 $Δ D E F$ 关于 $y$ 轴对称，已知点 $A (- 4 ， 6) ， B (- 6 ， 2) ， E (2 ， 1)$ ，则点 $C$ 的坐标，点 $D$ 的坐标，点 $F$ 的坐标．

查看试题解析
12. 利用图或图两个图形中的有关面积的等量关系都能证明数学中一个十分著名的定理，这个定理称为，该定理的结论其数学表达式是.

查看试题解析
13. 已知等腰三角形的一条腰长是5，底边长是6，则底边上的高为．

查看试题解析
14. 如图，正方形 $A B C D$ 的边长为 $6$ ，点 $A$ 的坐标为 $(- 1 ， 1) ， A B$ 平行于 $x$ 轴， $B C$ 平行于 $y$ 轴，则点 $B$ 的坐标为，点 $C$ 的坐标为，点 $D$ 的坐标为

查看试题解析
15. 如图，在平面直角坐标系中， $A (3 ， 0) ， B (0 ， 4)$ ，以点 $A$ 为圆心， $A B$ 为半径画弧，交 $x$ 轴的负半轴于点 $C$ ，则点 $C$ 的坐标为

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为 $1$ ，其面积标记为 $S_{1}$ ，以 $C D$ 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为 $S_{2} ···$ ，按照此规律继续下去，则 $S_{5}$ 的值为

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt[3]{\frac{37}{64} - 1}$

(2)、二选一： $| 3 - π | + \sqrt{{(4 - π)}^{2}}$ 或 $\sqrt{196} + \sqrt[3]{8} - \sqrt{169}$

查看试题解析
18. 计算：

(1)、 $(5 + \sqrt{6}) (\sqrt{2} - \sqrt{3})$

(2)、 $\frac{10 \sqrt{48} - 6 \sqrt{27} + 4 \sqrt{12}}{\sqrt{12}}$

查看试题解析
19. 计算： $\frac{1}{3} \sqrt{18} + 6 \sqrt{\frac{1}{3}} + \sqrt{\frac{1}{2}}$

查看试题解析
20. 如图，每个小正方形的边长是 $1$ ，在下面图①中画出一个面积是 $2$ 的直角三角形；在图②中画出一个面积是 $2$ 的正方形．(所画直角三角形与正方形的顶点均为网格线的交点)

查看试题解析
21. $Δ A B C$ 在直角坐标系中的位置如图所示，(小正方形网格的边长为1个单位长度， $Δ A B C$ 顶点是网格线的交点)．

(1)、写出 $Δ A B C$ 的各顶点坐标；

(2)、请画出 $Δ A B C$ 关于 $x$ 轴对称的 $Δ A_{1} B_{1} C_{1}$ 并写出 $Δ A_{1} B_{1} C_{1}$ 的各顶点坐标．

查看试题解析
22. 如图，在四边形 $A B C D$ 中， $A C ⊥ C D ， Δ A D C$ 的面积是 $30 c m^{2} ， D C = 12 c m ， A B = 3 c m ， B C = 4 c m ，$

(1)、求 $A D$ 的长；

(2)、求 $Δ A B C$ 的面积.

查看试题解析
23. 如图，将长AB=5cm，宽AD=3cm的长方形纸片ABCD折叠，使点A与C重合，折痕为EF，则AE长是多少？

查看试题解析
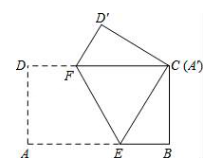24. 嘉嘉参加机器人设计活动，需操控机器人在5×5的方格棋盘上从A点行走至B点，且每个小方格皆为正方形，主办单位规定了三条行走路径R₁ ， R₂ ， R₃ ，其行经位置如图与表所示：
路径
编号
图例
行径位置
第一条路径
R₁
_
A→C→D→B
第二条路径
R₂
…
A→E→D→F→B
第三条路径
R₃
▂
A→G→B
已知A、B、C、D、E、F、G七点皆落在格线的交点上，且两点之间的路径皆为直线，在无法使用任何工具测量的条件下，请判断R₁、R₂、R₃这三条路径中，最长与最短的路径分别为何？请写出你的答案，并完整说明理由．

查看试题解析

路径	编号	图例	行径位置
第一条路径	R₁	_	A→C→D→B
第二条路径	R₂	…	A→E→D→F→B
第三条路径	R₃	▂	A→G→B