辽宁省鞍山市岫岩县2020-2021学年八年级上学期数学期中试卷
试卷更新日期：2021-08-23 类型：期中考试
一、单选题
-
1. 如下字体的四个汉字中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知三角形两边的长分别是3和7，则此三角形第三边的长可能是（ ）A、1 B、2 C、8 D、113. 下列生产和生活：①用人字架来建筑房屋；②用窗钩来固定窗扇；③在栅栏门上斜钉着一根木条；④商店的推拉活动防盗门等．其中，用到三角形的稳定性的有（ ）A、1种 B、2种 C、3种 D、4种4. 如图，在△ABC中，AB=AC，△ADE的顶点D，E分别在BC，AC上，且∠DAE=90°，AD=AE．若∠C+∠BAC=145°，则∠EDC的度数为（ ）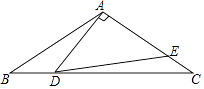
A、17.5° B、12.5° C、12° D、10°5. 若一个多边形的各内角都相等，则一个内角与一个外角的度数之比不可能是( )A、2：1 B、1：1 C、5：2 D、5：46. 如图所示，将矩形纸片ABCD折叠，使点D与点B重合，点C落在点C′处，折痕为EF，若∠EFC′＝125°，那么∠ABE的度数为（ ）
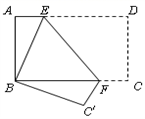A、15° B、20° C、25° D、30°7. 如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6 cm，AB的垂直平分线交BC于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN的长为 （ ）
A、4 cm B、3 cm C、2 cm D、1 cm8. 如图，已知∠BOF=120°，则∠A+∠B+∠C+∠D+∠E+∠F为多少度（ ）
A、360° B、720° C、540° D、240°9.如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于 MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（ ）
A、15 B、30 C、45 D、6010. 如图，在Rt△ABC中，∠BAC＝90°，AB＝AC ， 点D为BC中点，直角MDN绕点旋转，DM、DN分别与边AB ， AC交于E、F两点，下列结论：①△DEF是等腰直角三角形； ②AE＝CF； ③△BDE≌△ADF； ④BE+CF＝EF ． 其中正确的是（ ）
A、①②④ B、②③④ C、①②③ D、①②③④二、填空题
-
11. 如图，在△ABC中，∠C＝90°，BD＝6cm ， AD平分∠BAC ， BC＝10cm ， 则点D到AB的距离为 ．
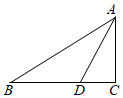12. 如图，在 ABC中，BC边的垂直平分线交BC于D，交AB于E，若CE平分∠ACB，∠B=40°则∠A=度．
13. 在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有种．
14. 如图， ， 是 延长线上的一点， ，动点 从点 出发沿 以 的速度移动，动点 从点 发沿 以 的速度移动，如果点 同时出发，用 表示移动的时间，当 时， 是等腰三角形.
15. 如图，把三角形铁皮ABC加工成四边形ABCD形状的零件，∠A＝40°，且D恰好是△ABC两条角平分线的交点，工人师傅量得∠BDC＝110°，则这个四边形零件加工 ． （填“合格”或“不合格”）
16. 如图，△ABC中，∠A：∠ABC：∠ACB＝3：5：10，又△A′B′C≌△ABC ， 则∠BCA′：∠BCB′的值为 ．
17. 小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒的长度分别是： ， ， （单位：cm）．18. 已知甲船从A处向正北方向航行，乙船在A处北偏西80°的B处，则乙船向方向航行，两船正好能够相遇．（已知两船的速度相同，起始时间相同）19. 观察规律：1＝12；1+3＝22；1+3+5＝32；1+3+5+7＝42…则1+3+5+7+9+…+2013＝ ．20. 如图，AB=12m，CA⊥AB于点A，DB⊥AB于点B，且AC=4m，点P从点B以1m/min的速度向点A运动；点Q从点B以2m/min的速度向点D运动，P，Q两点同时出发，运动min时，△CAP与△PBQ全等．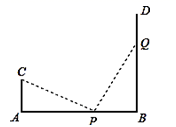
三、解答题
-
21. 如图，BA、BC是两条公路，在两条公路夹角内部的点P处有一油库，若在两公路上分别建个加油站，并使运油的油罐车从油库出发先到一加油站，再到另一加油站，最后回到油库的路程最短，则加油站应如何选址？
22. 已知：如图，AB=AE，∠1=∠2，∠B=∠E．求证：BC=ED．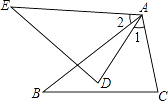
23.如图，在五边形ABCDE中，∠BCD=∠EDC=90°，BC=ED，AC=AD．
(1)、求证：△ABC≌△AED；(2)、当∠B=140°时，求∠BAE的度数．24. 如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．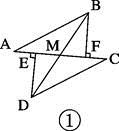
(1)、求证：MB=MD，ME=MF(2)、当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．25. 阅读下面的题目及分析过程，并按要求进行证明．已知：如图，点E是BC的中点，点A在DE上，且∠BAE＝∠CDE ．
求证：AB＝CD ．
分析：证明两条线段相等，常用的方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等，因此，要证AB＝CD ， 必须添加适当的辅助线，构造全等三角形或等腰三角形．
(1)、现给出如下两种添加辅助线的方法，请任意选出其中一种，对原题进行证明．①如图1，延长DE到点F ， 使EF＝DE ， 连接BF；
②如图2，分别过点B、C作BF⊥DE ， CG⊥DE ， 垂足分别为点F ， G ．
(2)、请你在图3中添加不同于上述的辅助线，并对原题进行证明．26. 在△ABC中，若AD是∠BAC的角平分线，点E和点F分别在AB和AC上，且DE⊥AB ， 垂足为E ， DF⊥AC ， 垂足为F（如图（1）），则可以得到以下两个结论：①∠AED+∠AFD＝180°；②DE＝DF ．
那么在△ABC中，仍然有条件“AD是∠BAC的角平分线，点E和点F ， 分别在AB和AC上”，请探究以下两个问题：
(1)、若∠AED+∠AFD＝180°（如图（2）），则DE与DF是否仍相等？若仍相等，请证明；否则请举出反例．(2)、若DE＝DF ， 则∠AED+∠AFD＝180°是否成立？（只写出结论，不证明）