辽宁省鞍山市铁东区2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-08-23 类型:期中考试
一、单选题
-
1. 下列图形中一定是轴对称图形的是( )A、
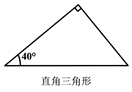 B、
B、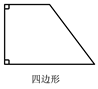 C、
C、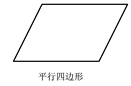 D、
D、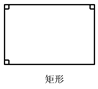 2. 三角形的两边长分别为2cm和4cm , 则下列长度的四条线段中不能作为第三边的是( )A、3cm B、4cm C、5cm D、6cm3. 下面四个图形中,线段BD是△ABC的高的图形是( )A、
2. 三角形的两边长分别为2cm和4cm , 则下列长度的四条线段中不能作为第三边的是( )A、3cm B、4cm C、5cm D、6cm3. 下面四个图形中,线段BD是△ABC的高的图形是( )A、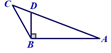 B、
B、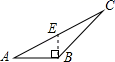 C、
C、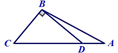 D、
D、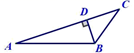 4. 如图,①以点O为圆心,适当长为半径画弧,分别交OM、ON于A、C两点;②再分别以A,C为圆心,以大于 AC长为半径画弧,两弧在∠MON内部交于点B;③作射线OB,则OB为∠MON的角平分线的依据为( )
4. 如图,①以点O为圆心,适当长为半径画弧,分别交OM、ON于A、C两点;②再分别以A,C为圆心,以大于 AC长为半径画弧,两弧在∠MON内部交于点B;③作射线OB,则OB为∠MON的角平分线的依据为( ) A、SAS B、SSS C、HL D、ASA5. 如图,△ABC 中,AB = 6cm ,AC = 8cm ,BC 的垂直平分线l 与 AC 相交于点 D ,则DABD 的周长为( )
A、SAS B、SSS C、HL D、ASA5. 如图,△ABC 中,AB = 6cm ,AC = 8cm ,BC 的垂直平分线l 与 AC 相交于点 D ,则DABD 的周长为( ) A、10cm B、12cm C、14cm D、16cm6. 如图,AC=DE,∠1=∠2,添加一个条件.不能判定△ABC≌△DFE的条件是( )
A、10cm B、12cm C、14cm D、16cm6. 如图,AC=DE,∠1=∠2,添加一个条件.不能判定△ABC≌△DFE的条件是( ) A、∠A=∠D B、AB=DF C、BC=FE D、∠B=∠F7. 如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( )
A、∠A=∠D B、AB=DF C、BC=FE D、∠B=∠F7. 如图,△ABC≌△DEC,B、C、D在同一直线上,且CE=5,AC=7,则BD长( ) A、12 B、7 C、2 D、148. 如图,点A在直线MN上,点B在直线MN上方,点P为直线MN上一动点,当△ABP为等腰三角形时,则满足条件的点P的个数为( )
A、12 B、7 C、2 D、148. 如图,点A在直线MN上,点B在直线MN上方,点P为直线MN上一动点,当△ABP为等腰三角形时,则满足条件的点P的个数为( ) A、1 B、3 C、4 D、5
A、1 B、3 C、4 D、5二、填空题
-
9. 七边形ABCDEFG的内角和的度数为 .10. 如图,AD、BC表示两根长度相同的木条,若O是AD、BC的中点,经测量AB=9cm,则容器的内径CD为 cm.
 11. 如图,在Rt△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,其中CE=4.5,AB=10,那么△ABE的面积为 .
11. 如图,在Rt△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,其中CE=4.5,AB=10,那么△ABE的面积为 . 12. 已知一个等腰三角形的一个内角为 ,则它的顶角等于 .13. 如图,在△ABC中,点D为AB延长线上一点,点E为AC中点,过C作CF//AB交射线DE于F , 若BD=1,CF=5,则AB的长度为 .
12. 已知一个等腰三角形的一个内角为 ,则它的顶角等于 .13. 如图,在△ABC中,点D为AB延长线上一点,点E为AC中点,过C作CF//AB交射线DE于F , 若BD=1,CF=5,则AB的长度为 . 14. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=.
14. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B=. 15. 如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为 .
15. 如图,在△ABC中,BD平分∠ABC,连接CD,若∠A=∠D=40°,∠ACD=30°,则∠DCE的度数为 . 16. 如图,在等边三角形ABC中,AD⊥BC,垂足为D,点P为AB边上一点,EF垂直平分线段BP,EF与线段AD交于F,连接CF、PF,以下结论:①PF=CF;②∠PFC=120°,③∠PFE+∠ACF=90°;④∠PFA=∠DCF.其中一定正确的有 . (填序号即可)
16. 如图,在等边三角形ABC中,AD⊥BC,垂足为D,点P为AB边上一点,EF垂直平分线段BP,EF与线段AD交于F,连接CF、PF,以下结论:①PF=CF;②∠PFC=120°,③∠PFE+∠ACF=90°;④∠PFA=∠DCF.其中一定正确的有 . (填序号即可)
三、解答题
-
17. 如图,在直角坐标系中,A(﹣1,5),B(﹣3,0),C(﹣4,3).
⑴在图中作出△ABC关于y轴对称的图形△A1B1C1 , 并写出点C1的坐标;
⑵点P是x轴上一动点,画出点P,使得CP+A1P取最小值.
 18. 已知,如图,∠B=60°,AB//DE,EC=ED,求证:△DEC为等边三角形.
18. 已知,如图,∠B=60°,AB//DE,EC=ED,求证:△DEC为等边三角形. 19. 如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=48°,∠C=62°,求∠ABE的度数.
19. 如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=48°,∠C=62°,求∠ABE的度数.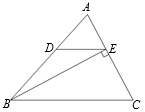 20. 如图,在△ABC和△ADE中,AB=AC , AD=AE , ∠BAC=∠DAE , 求证:△ABD≌△ACE .
20. 如图,在△ABC和△ADE中,AB=AC , AD=AE , ∠BAC=∠DAE , 求证:△ABD≌△ACE . 21. 如图,在△ABC中,AB=AC , ∠B=65°,D为BC上一点,BF=CD , CE=BD , 求∠EDF的度数.
21. 如图,在△ABC中,AB=AC , ∠B=65°,D为BC上一点,BF=CD , CE=BD , 求∠EDF的度数. 22. 如图,在△ABC中,CD平分∠ACB , CD交AB边于点D , 过D作DE//BC交AC边于点E , 若DE恰好平分∠ADC , DB=5,EC=3,求△EDC的周长.
22. 如图,在△ABC中,CD平分∠ACB , CD交AB边于点D , 过D作DE//BC交AC边于点E , 若DE恰好平分∠ADC , DB=5,EC=3,求△EDC的周长. 23. 如图,在等边三角形ABC中,点D为BC边上一点,DE//AB,过D作DF⊥DE交AB于点F,且∠EFD=60°,CN平分∠ACB,CN分别交DE、EF于M、N两点.
23. 如图,在等边三角形ABC中,点D为BC边上一点,DE//AB,过D作DF⊥DE交AB于点F,且∠EFD=60°,CN平分∠ACB,CN分别交DE、EF于M、N两点. (1)、求证:△CEN≌△EDF;(2)、求证:点N为线段EF中点.24. 如图,在△ABC中,∠BAC=45°,CD⊥AB,垂足为D,AE平分∠BAC,且AE交CD于点E,
(1)、求证:△CEN≌△EDF;(2)、求证:点N为线段EF中点.24. 如图,在△ABC中,∠BAC=45°,CD⊥AB,垂足为D,AE平分∠BAC,且AE交CD于点E, (1)、如图1,若AE=BC;
(1)、如图1,若AE=BC;①求证:△ADE≌△CDB;
②求证:AB=AC;
(2)、如图2,若AE≠BC,延长AE交BC于点H,过C作CG⊥AH分别交AH、AB于F、G两点,当DB=DE+CH时,求∠ACB的度数.