黑龙江省牡丹江市2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-08-23 类型:期中考试
一、单选题
-
1. 下列对称图形中,是轴对称图形有________个( )
 A、1 B、2 C、3 D、42. 如图,王师傅用六根木条钉成一个六边形木框,要使它不变形,至少还要再钉上________根木条( )
A、1 B、2 C、3 D、42. 如图,王师傅用六根木条钉成一个六边形木框,要使它不变形,至少还要再钉上________根木条( )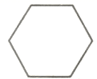 A、2 B、3 C、4 D、53. 等腰三角形周长为36cm,两边长之比为 ,则底边长为( )A、16cm B、4cm C、4cm或24cm D、16cm或4cm4. 具备下列条件的三角形中,不是直角三角形的是( )A、 B、 C、 D、5. 如图,在 中,DE是AC的垂直平分线,交AC边于E , 交BC边于D , 连接AD,若 , 的周长为13,则 的周长( )
A、2 B、3 C、4 D、53. 等腰三角形周长为36cm,两边长之比为 ,则底边长为( )A、16cm B、4cm C、4cm或24cm D、16cm或4cm4. 具备下列条件的三角形中,不是直角三角形的是( )A、 B、 C、 D、5. 如图,在 中,DE是AC的垂直平分线,交AC边于E , 交BC边于D , 连接AD,若 , 的周长为13,则 的周长( )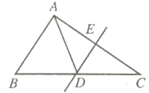 A、16 B、19 C、20 D、246. 如图, ,点D在AC边上,AE和BD相交于点O,若 , ,则 的度数为( )
A、16 B、19 C、20 D、246. 如图, ,点D在AC边上,AE和BD相交于点O,若 , ,则 的度数为( )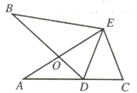 A、45° B、40° C、35° D、30°7. 如图,图中的阴影部分是由5个小正方形组成的一个图形,若在图中的方格里再涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( )
A、45° B、40° C、35° D、30°7. 如图,图中的阴影部分是由5个小正方形组成的一个图形,若在图中的方格里再涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( ) A、3种 B、4种 C、5种 D、6种8. 如图,在 中, ,点 I是 、 的平分线的交点.点D是 、 的两条外角平分线的交点,点E是内角 、外角 的平分线的交点,则下列结论 错误的是( )
A、3种 B、4种 C、5种 D、6种8. 如图,在 中, ,点 I是 、 的平分线的交点.点D是 、 的两条外角平分线的交点,点E是内角 、外角 的平分线的交点,则下列结论 错误的是( )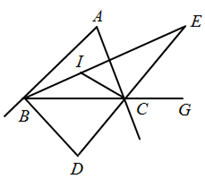 A、 B、 C、 D、9. 在平面直角坐标系中,点A的坐标为 ,那么下列说法错误的是( )A、点A与点 关于x轴对称 B、点A与点 关于y轴对称 C、点A与点 关于直线 对称 D、点A与点 关于直线 对称10. 如图,已知AD为 的高线, ,以AB为底边作等腰 ,连接ED,EC延长CE交AD于F点,下列结论:① ;② ;③ ;④ 为等腰三角形;⑤ ,其中正确的有( )
A、 B、 C、 D、9. 在平面直角坐标系中,点A的坐标为 ,那么下列说法错误的是( )A、点A与点 关于x轴对称 B、点A与点 关于y轴对称 C、点A与点 关于直线 对称 D、点A与点 关于直线 对称10. 如图,已知AD为 的高线, ,以AB为底边作等腰 ,连接ED,EC延长CE交AD于F点,下列结论:① ;② ;③ ;④ 为等腰三角形;⑤ ,其中正确的有( )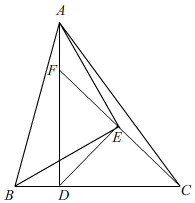 A、①③⑤ B、①②④ C、①③④ D、①②③⑤
A、①③⑤ B、①②④ C、①③④ D、①②③⑤二、填空题
-
11.
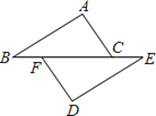
如图,点B、F、C、E在同一条直线上,点A、D在直线BE的两侧,AB∥DE,BF=CE,请添加一个适当的条件: ,使得AC=DF.
 12. 若点 与点 关于x轴对称,则 .13. 如图,则 的度数为 .
12. 若点 与点 关于x轴对称,则 .13. 如图,则 的度数为 .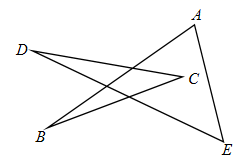 14. 已知三角形三边长分别为m,n,k , 且m、n满足 ,则这个三角形最长边k的取值范围是 .15. 如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是度.
14. 已知三角形三边长分别为m,n,k , 且m、n满足 ,则这个三角形最长边k的取值范围是 .15. 如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是度.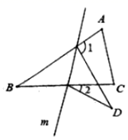 16. 如图,点D,E,F分别是边BC,AD,AC上的中点,若图中阴影部分的面积为3,则 的面积是 .
16. 如图,点D,E,F分别是边BC,AD,AC上的中点,若图中阴影部分的面积为3,则 的面积是 .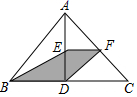 17. 如图(1),已知 ,D为 的角平分线上一点,连接BD,CD;如图(2),已知 ,D,E为 的角平分线上两点,连接BD,CD,BE,CE;如图(3),已知 ,D,E , F为 的角平分线上三点,连接BD,CD,BE,CE,BF,CF;……,依此规律,第7个图形中有全等三角形的对数是 .
17. 如图(1),已知 ,D为 的角平分线上一点,连接BD,CD;如图(2),已知 ,D,E为 的角平分线上两点,连接BD,CD,BE,CE;如图(3),已知 ,D,E , F为 的角平分线上三点,连接BD,CD,BE,CE,BF,CF;……,依此规律,第7个图形中有全等三角形的对数是 .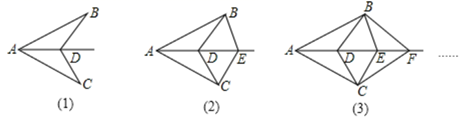 18. 小明同学在用计算器计算某 边形的内角和时,不小心多输入一个内角,得到和为 ,则 等于.19. 如图,已知 ,点E为CD上一点,AE,BE分别平分 , .若 , ,则四边形ABCD的面积是 .
18. 小明同学在用计算器计算某 边形的内角和时,不小心多输入一个内角,得到和为 ,则 等于.19. 如图,已知 ,点E为CD上一点,AE,BE分别平分 , .若 , ,则四边形ABCD的面积是 .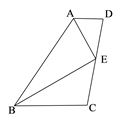 20. 如图, ,垂足为点A , 射线 ,垂足为点B , , .动点E从A点出发以3cm/s的速度沿射线AN运动,动点D在射线BM上,随着 E点运动而运动,始终保持 .若点E的运动时间为 ,则当 个秒时, 与 全等.
20. 如图, ,垂足为点A , 射线 ,垂足为点B , , .动点E从A点出发以3cm/s的速度沿射线AN运动,动点D在射线BM上,随着 E点运动而运动,始终保持 .若点E的运动时间为 ,则当 个秒时, 与 全等.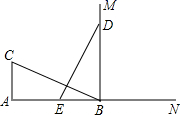
三、解答题
-
21. 已知一个多边形的内角和比它的外角和的2倍还大180°,求这个多边形共有多少条对角线.22. 如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=32°,∠AEB=70°.
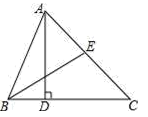 (1)、求∠CAD的度数;(2)、若点F为线段BC上任意一点,当△EFC为直角三角形时,则∠BEF的度数为23. 已知在 中, , ,直线l绕点C旋转,过点A作 于D , 过点B作 于E , 若 , ,画图并直接写出DE的长.24. 已知平面直角坐标系xOy中,点A,B,C的坐标分别为 、 、 .
(1)、求∠CAD的度数;(2)、若点F为线段BC上任意一点,当△EFC为直角三角形时,则∠BEF的度数为23. 已知在 中, , ,直线l绕点C旋转,过点A作 于D , 过点B作 于E , 若 , ,画图并直接写出DE的长.24. 已知平面直角坐标系xOy中,点A,B,C的坐标分别为 、 、 .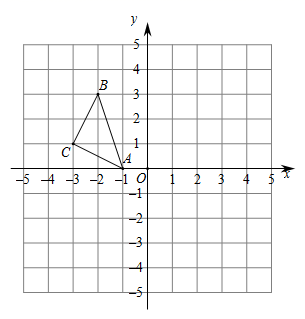 (1)、作出 关于y轴对称的 ,直接写出 , 两点的坐标: ( ), ( );(2)、直接写出 的面积, ;(3)、若点 与点Q关于y轴对称,且 ,则点P的坐标 .25. 已知 为等腰直角三角形, , 为等腰直角三角形, ,点D在直线BC上,连接CE.
(1)、作出 关于y轴对称的 ,直接写出 , 两点的坐标: ( ), ( );(2)、直接写出 的面积, ;(3)、若点 与点Q关于y轴对称,且 ,则点P的坐标 .25. 已知 为等腰直角三角形, , 为等腰直角三角形, ,点D在直线BC上,连接CE.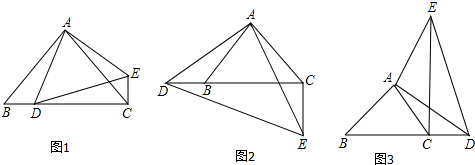 (1)、若点D在线段BC上,如图1,求证: ;(2)、若D在CB延长线上,如图2,若D在BC延长线上,如图3,其他条件不变,又有怎样的结论?请分别写出你发现的结论,不需要证明;(3)、若 , ,则BC的长为 .26. 在平面直角坐标系中,点A坐标 ,点B坐标 ,点 C为x轴正半轴上一动点,过点A作 交y轴于点E.
(1)、若点D在线段BC上,如图1,求证: ;(2)、若D在CB延长线上,如图2,若D在BC延长线上,如图3,其他条件不变,又有怎样的结论?请分别写出你发现的结论,不需要证明;(3)、若 , ,则BC的长为 .26. 在平面直角坐标系中,点A坐标 ,点B坐标 ,点 C为x轴正半轴上一动点,过点A作 交y轴于点E.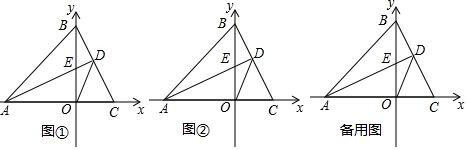 (1)、如图①,若点C的坐标为 ,求点E的坐标;(2)、如图②,若点C在x轴正半轴上运动,且 ,其它条件不变,连接DO , 求证:DO平分 ;(3)、若点C在x轴正半轴上运动,当 时,则 的度数为 .
(1)、如图①,若点C的坐标为 ,求点E的坐标;(2)、如图②,若点C在x轴正半轴上运动,且 ,其它条件不变,连接DO , 求证:DO平分 ;(3)、若点C在x轴正半轴上运动,当 时,则 的度数为 .