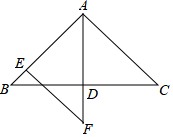
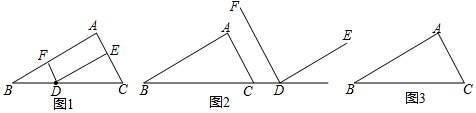
河北省张家口市涿鹿县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-08-23 类型:期中考试
一、单选题
-
1. 下列图形具有稳定性的是( )A、
 B、
B、 C、
C、 D、
D、 2. 三角形一边上的中线把原三角形分成两个( )A、形状相同的三角形 B、面积相等的三角形 C、直角三角形 D、周长相等的三角形3. 下列图标,是轴对称图形的是( )
2. 三角形一边上的中线把原三角形分成两个( )A、形状相同的三角形 B、面积相等的三角形 C、直角三角形 D、周长相等的三角形3. 下列图标,是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 4. 已知点 , ,则( )A、A、B关于x轴对称 B、A、B关于y轴对称 C、直线AB平行于x轴 D、直线AB垂直于y轴5.
4. 已知点 , ,则( )A、A、B关于x轴对称 B、A、B关于y轴对称 C、直线AB平行于x轴 D、直线AB垂直于y轴5.下列图形中与已知图形全等的是( )
 A、
A、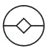 B、
B、 C、
C、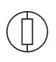 D、
D、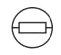 6. 三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
6. 三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )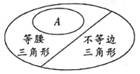 A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形7. 如图,两个三角形是全等三角形,x的值是( )
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形7. 如图,两个三角形是全等三角形,x的值是( )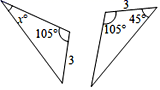 A、30° B、45° C、50° D、85°8. 如图,线段AB与 ( )不关于直线l成轴对称的是( )A、
A、30° B、45° C、50° D、85°8. 如图,线段AB与 ( )不关于直线l成轴对称的是( )A、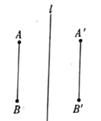 B、
B、 C、
C、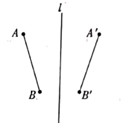 D、
D、 9. 根据如图所示的尺规作图痕迹判断,下列结论错误的是( )
9. 根据如图所示的尺规作图痕迹判断,下列结论错误的是( )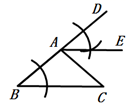 A、∠DAE=∠B B、∠C=∠EAC C、∠DAE=∠EAC D、AE∥BC10. 图中的小正方形边长都相等,若 ,则点Q可能是图中的( )
A、∠DAE=∠B B、∠C=∠EAC C、∠DAE=∠EAC D、AE∥BC10. 图中的小正方形边长都相等,若 ,则点Q可能是图中的( ) A、点D B、点C C、点B D、点A11. 如图,BE、CF都是△ABC的角平分线,且∠BDC=130°,则∠A=( )
A、点D B、点C C、点B D、点A11. 如图,BE、CF都是△ABC的角平分线,且∠BDC=130°,则∠A=( )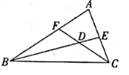 A、50° B、60° C、70° D、80°12. 一辆模型赛车,先前进1m,然后沿原地逆时针方向旋转,旋转角为α(0<α<90°),被称为一次操作,若五次操作后,发现赛车回到出发点,则旋转角α为( )A、 B、 C、 D、13. 对于 嘉淇用尺规进行了如下操作如图:
A、50° B、60° C、70° D、80°12. 一辆模型赛车,先前进1m,然后沿原地逆时针方向旋转,旋转角为α(0<α<90°),被称为一次操作,若五次操作后,发现赛车回到出发点,则旋转角α为( )A、 B、 C、 D、13. 对于 嘉淇用尺规进行了如下操作如图:⑴分别以点B和点C为圆心,BA,CA为半径作弧,两弧相交于点D;⑵作直线AD交BC边于点E,根据嘉淇的操作方法,可知线段AE是( )
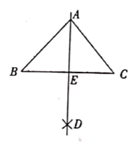 A、边BC的垂直平分线 B、 的中线 C、 的高线 D、 的角平分线14. 如图,DE、FG分别是△ABC的AB、AC边上的垂直平分线,且∠BAC=100°,那么∠DAF的度数为( )
A、边BC的垂直平分线 B、 的中线 C、 的高线 D、 的角平分线14. 如图,DE、FG分别是△ABC的AB、AC边上的垂直平分线,且∠BAC=100°,那么∠DAF的度数为( )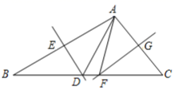 A、10° B、20° C、30° D、40°
A、10° B、20° C、30° D、40°二、填空题
-
15. 若一个等腰三角形的顶角等于 ,则它底角等于 .16.
某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是 ,理由是
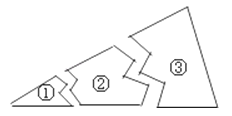 17. 如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离 .
17. 如图,上午8时,一条船从A处出发,以15海里/时的速度向正北航行,10时到达B处,从A、B望灯塔C,测得∠NAC=42°,∠NBC=84°,则从B处到灯塔C的距离 .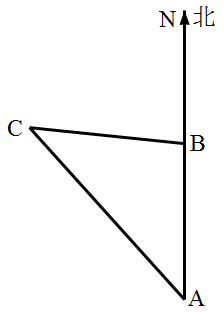 18. 如图,在△ABC 中,已知点 D、E、F 分别是边 BC、AD、CE 上的中点,且 S△ABC=4, 则 S△BEF= .
18. 如图,在△ABC 中,已知点 D、E、F 分别是边 BC、AD、CE 上的中点,且 S△ABC=4, 则 S△BEF= .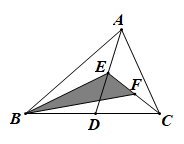 19. 阅读材料:连接多边形的对角线或在多边形边上(非顶点)取一点或在多边形内部取一点与多边形各顶点的连线,能将多边形分割成若干个小三角形,图1给出了四边形的具体分割方法,分别将四边形分割成了2个、3个、4个小三角形.
19. 阅读材料:连接多边形的对角线或在多边形边上(非顶点)取一点或在多边形内部取一点与多边形各顶点的连线,能将多边形分割成若干个小三角形,图1给出了四边形的具体分割方法,分别将四边形分割成了2个、3个、4个小三角形.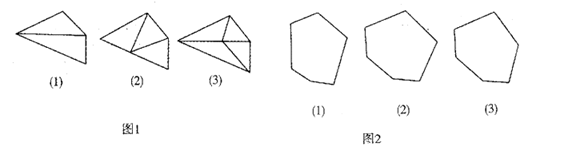 (1)、请你按照上述方法将图2中的六边形进行分割,并写出每种方法所得到的小三角形的个数为个、个,个(2)、当多边形为n边形时,按照上述方法进行分割,写出每种分法所得到的小三角形的个数为个、个,个
(1)、请你按照上述方法将图2中的六边形进行分割,并写出每种方法所得到的小三角形的个数为个、个,个(2)、当多边形为n边形时,按照上述方法进行分割,写出每种分法所得到的小三角形的个数为个、个,个三、解答题
-
20. 如图,在△ABC中,AD⊥BC , AE平分∠BAC , ∠B=72°,∠C=30°,
①求∠BAE的度数;
②求∠DAE的度数.
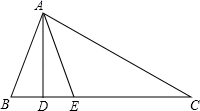 21. 用一条长18cm的铁丝围成一个等腰三角形,其中三边长分别为4cm,xcm,ycm,求x,y的值。22. 如图,已知点 在 上,且 求证:
21. 用一条长18cm的铁丝围成一个等腰三角形,其中三边长分别为4cm,xcm,ycm,求x,y的值。22. 如图,已知点 在 上,且 求证: