广东省韶关市新丰县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-08-23 类型:期中考试
一、单选题
-
1. 下列图形具有稳定性的是( )A、
 B、
B、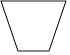 C、
C、 D、
D、 2. 下列图形中,是轴对称图形的是( )A、
2. 下列图形中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 已知三角形的两边长分别为1cm和4cm , 则下列长度的四条线段中能作为第三边的是( )A、3cm B、4cm C、5cm D、6cm4. 如图,△ABC的外角∠CAE为115°,∠C=80°, 则∠B的度数为( )
3. 已知三角形的两边长分别为1cm和4cm , 则下列长度的四条线段中能作为第三边的是( )A、3cm B、4cm C、5cm D、6cm4. 如图,△ABC的外角∠CAE为115°,∠C=80°, 则∠B的度数为( )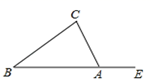 A、55° B、45° C、35° D、30°5. 已知一个n边形的每个外角都等于 ,则n的值是A、5 B、6 C、7 D、86. 如图,△ACE≌△DBF , AE DF , AB=3,BC=2,则AD的长度等于( )
A、55° B、45° C、35° D、30°5. 已知一个n边形的每个外角都等于 ,则n的值是A、5 B、6 C、7 D、86. 如图,△ACE≌△DBF , AE DF , AB=3,BC=2,则AD的长度等于( )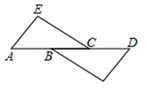 A、2 B、8 C、9 D、107. 设AD是 的中线,则( )A、 B、 C、 D、8. 如图,在△ABC中,∠B=65°,过点C作CD∥AB,∠ACD=40°,则∠ACB的度数为( )
A、2 B、8 C、9 D、107. 设AD是 的中线,则( )A、 B、 C、 D、8. 如图,在△ABC中,∠B=65°,过点C作CD∥AB,∠ACD=40°,则∠ACB的度数为( ) A、60° B、65° C、70° D、75°9. 在平面直角坐标系中,点P(a , )关于x轴对称点为Q(3,b),则 的值为( )A、-1 B、1 C、-2 D、210. 如图,在△ABC中,∠ABC=45°,AC=9cm , F是高AD和BE的交点,则BF的长是( )
A、60° B、65° C、70° D、75°9. 在平面直角坐标系中,点P(a , )关于x轴对称点为Q(3,b),则 的值为( )A、-1 B、1 C、-2 D、210. 如图,在△ABC中,∠ABC=45°,AC=9cm , F是高AD和BE的交点,则BF的长是( )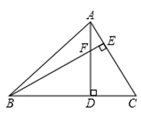 A、4cm B、6cm C、8cm D、9cm
A、4cm B、6cm C、8cm D、9cm二、填空题
-
11. 如图,在Rt△ABC中,∠C=90°,CD⊥AB,垂足为D.若∠A=32°,则∠BCD=°.
 12. 如图,△ABC≌△ADE , 且∠EAB=120°,∠CAD=10°,∠CAB=°.
12. 如图,△ABC≌△ADE , 且∠EAB=120°,∠CAD=10°,∠CAB=°.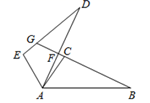 13. 如图,在 中, ,AD平分 交BC于点D,若 , ,则 的面积为.
13. 如图,在 中, ,AD平分 交BC于点D,若 , ,则 的面积为.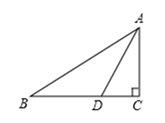 14. 如图,在 中, 的垂直平分线分别交 、 于点E、F.若 是等边三角形,则 °.
14. 如图,在 中, 的垂直平分线分别交 、 于点E、F.若 是等边三角形,则 °. 15. 如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有个。
15. 如图,3×3方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有个。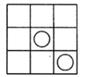 16. 如图,AB=AD , ∠1=∠2,要得到△ABC≌△ADE , 添加一个条件可以是 .
16. 如图,AB=AD , ∠1=∠2,要得到△ABC≌△ADE , 添加一个条件可以是 .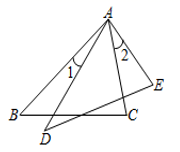 17. 如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED , 则图中∠1+∠2的度数为°.
17. 如图,在一个三角形的纸片(△ABC)中,∠C=90°,将这个纸片沿直线DE剪去一个角后变成一个四边形ABED , 则图中∠1+∠2的度数为°.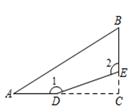
三、解答题
-
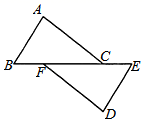
18. 如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BC=EF,求证AB∥DE.
 19. 要测量河两岸相对的两点A , B的距离,先在AB的垂线BF上取两点C , D , 使CD=BC , 再定出BF的垂线DE , 使A , C , E在一条直线上(如图所示), 可以说明△EDC≌△ABC , 得ED=AB , 因此测得ED的长就是AB的长,请你运用自己所学知识说明他们的做法是正确的.
19. 要测量河两岸相对的两点A , B的距离,先在AB的垂线BF上取两点C , D , 使CD=BC , 再定出BF的垂线DE , 使A , C , E在一条直线上(如图所示), 可以说明△EDC≌△ABC , 得ED=AB , 因此测得ED的长就是AB的长,请你运用自己所学知识说明他们的做法是正确的.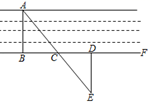 20. 如图,△ABC中,∠ABC=∠C=70°,BD平分∠ABC,求∠ADB的度数.
20. 如图,△ABC中,∠ABC=∠C=70°,BD平分∠ABC,求∠ADB的度数.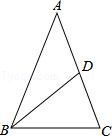 21. 如图,已知AB=DC , AB CD , E、F是AC上两点,且AF=CE .(1)、求证:△ABE≌△CDF;(2)、若∠BCE=30°,∠CBE=70°,求∠CFD的度数.22. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.
21. 如图,已知AB=DC , AB CD , E、F是AC上两点,且AF=CE .(1)、求证:△ABE≌△CDF;(2)、若∠BCE=30°,∠CBE=70°,求∠CFD的度数.22. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.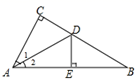 (1)、求∠B的度数.(2)、若DE=5,求BC的长.23. 在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
(1)、求∠B的度数.(2)、若DE=5,求BC的长.23. 在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.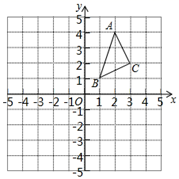 (1)、作出 关于x轴对称的 ;(2)、写出点C1的坐标;(3)、通过画图,在y轴上找一个点D , 使得AD+BD最小.24. 如图,已知 和 均为等边三角形,且点 、 、 在同一条直线上,连接 、 ,交 和 分别于 、 点,连接 .
(1)、作出 关于x轴对称的 ;(2)、写出点C1的坐标;(3)、通过画图,在y轴上找一个点D , 使得AD+BD最小.24. 如图,已知 和 均为等边三角形,且点 、 、 在同一条直线上,连接 、 ,交 和 分别于 、 点,连接 .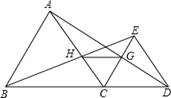 (1)、请说出 的理由;(2)、试说出 的理由;(3)、试猜想: 是什么特殊的三角形,并加以说明.25. 如图,已知 中, ,∠ABC=∠ACB, ,点 为 的中点.如果点 在线段 上以 的速度由点 向 点运动,同时,点 在线段 上由点 向 点运动,设点P运动的时间为t.
(1)、请说出 的理由;(2)、试说出 的理由;(3)、试猜想: 是什么特殊的三角形,并加以说明.25. 如图,已知 中, ,∠ABC=∠ACB, ,点 为 的中点.如果点 在线段 上以 的速度由点 向 点运动,同时,点 在线段 上由点 向 点运动,设点P运动的时间为t.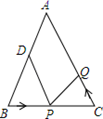 (1)、用含t的式子表示PC的长为;(2)、若点 的运动速度与点 的运动速度相等,经过1秒后, 与 是否全等,请说明理由.(3)、若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?
(1)、用含t的式子表示PC的长为;(2)、若点 的运动速度与点 的运动速度相等,经过1秒后, 与 是否全等,请说明理由.(3)、若点 的运动速度与点 的运动速度不相等,当点 的运动速度为多少时,能够使 与 全等?