广东省揭阳市普宁市2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2021-08-23 类型:期中考试
一、单选题
-
1. 下列各数中,不是无理数的是( )A、 B、 C、0.25 D、0.101001 0001…(相邻两个1之间0的个数逐次加1)2. 实数 的倒数是( )A、3 B、 C、﹣ D、3. 如图,在平面直角坐标系中,点A的坐标是( )
 A、(-2,-3) B、(3,-2) C、(2,3) D、(-2,3)4. 下列线段不能组成直角三角形的是( )A、6,8,10 B、1, , C、 ,1, D、2,4,5. 一次函数y=kx+3的图象经过点A(1,2),则其解析式为( )A、 B、y=﹣x+3 C、y=x+3 D、6. 若 +(a﹣4)2=0,则化简 的结果是( )A、 B、± C、 D、±7. 下列计算正确的是( )A、3 ﹣ =3 B、 =2 C、 D、 ÷ =38. 已知A、B两点的坐标分别是(﹣2,3)和(2,3),则下面四个结论:①点A在第四象限;②点B在第一象限;③线段AB平行于y轴;④点A、B之间的距离为4.其中正确的有( )A、①③ B、②③ C、②④ D、②③④9. 已知正比例函数y=kx的图象经过第一、三象限,则一次函数y=kx﹣k的图象可能是下图中的( )A、
A、(-2,-3) B、(3,-2) C、(2,3) D、(-2,3)4. 下列线段不能组成直角三角形的是( )A、6,8,10 B、1, , C、 ,1, D、2,4,5. 一次函数y=kx+3的图象经过点A(1,2),则其解析式为( )A、 B、y=﹣x+3 C、y=x+3 D、6. 若 +(a﹣4)2=0,则化简 的结果是( )A、 B、± C、 D、±7. 下列计算正确的是( )A、3 ﹣ =3 B、 =2 C、 D、 ÷ =38. 已知A、B两点的坐标分别是(﹣2,3)和(2,3),则下面四个结论:①点A在第四象限;②点B在第一象限;③线段AB平行于y轴;④点A、B之间的距离为4.其中正确的有( )A、①③ B、②③ C、②④ D、②③④9. 已知正比例函数y=kx的图象经过第一、三象限,则一次函数y=kx﹣k的图象可能是下图中的( )A、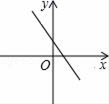 B、
B、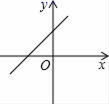 C、
C、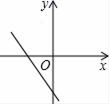 D、
D、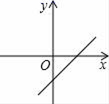 10. 如图,赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为 和 .若 ,大正方形的边长为5,则小正方形的边长为( )
10. 如图,赵爽弦图是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形两条直角边长分别为 和 .若 ,大正方形的边长为5,则小正方形的边长为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 16的平方根是 , 的立方根是 .12. 已知点A(a , ﹣ )与B( ,b)关于x轴对称,则ab= .13. 比较大小:﹣ ﹣2 .(填“ ”或“ ”)14. 以水平数轴的原点 为圆心过正半轴 上的每一刻度点画同心圆,将 逆时针依次旋转 、 、 、 、 得到 条射线,构成如图所示的“圆”坐标系,点 、 的坐标分别表示为 、 ,则点 的坐标表示为.
 15. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中l1 , l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系.小雨家去年用水量为160m3 , 若今年用水量与去年相同,水费将比去年多元.
15. 某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中l1 , l2分别表示去年、今年水费y(元)与用水量x(m3)之间的关系.小雨家去年用水量为160m3 , 若今年用水量与去年相同,水费将比去年多元. 16. 如图,一 蚂蚁沿着棱长为2的正方体表面从点 出发,经过2个侧面爬到点 ,如果它运动的路径是最短的,则最短路径长为 .
16. 如图,一 蚂蚁沿着棱长为2的正方体表面从点 出发,经过2个侧面爬到点 ,如果它运动的路径是最短的,则最短路径长为 . 17. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB+PA取最小值时,点P的坐标为 .
17. 如图,在平面直角坐标系中,点P是正比例函数y=x图象上的一点,点A的坐标为(0,1),点B的坐标为(4,1),当PB+PA取最小值时,点P的坐标为 .
三、解答题
-
18. 计算: ÷19. 我们已经知道 ,因此将 分子、分母同时乘以“ +3”,分母就变成了4.请仿照这种方法化简: .20. 如图,已知正比例函数y=kx经过点A , 点A在第四象限,过点A作AH⊥x轴,垂足为点H , 点A的横坐标为3,且△AOH的面积为3.求正比例函数的表达式.
 21. 十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
21. 十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损. (1)、请在图中画出平面直角坐标系,并标出景点C的位置;(2)、平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.22. 已知一次函数y=kx+b的图象与y轴的交点是(0,3),且过点(2,﹣1).
(1)、请在图中画出平面直角坐标系,并标出景点C的位置;(2)、平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.22. 已知一次函数y=kx+b的图象与y轴的交点是(0,3),且过点(2,﹣1). (1)、求该一次函数的解析式;(2)、画出该一次函数的图象,并根据图象回答:当x取何值时,一次函数y=kx+b的函数值大于3?23. 材料:海伦公式是利用三角形三条边长求三角形面积的公式,用符号表示为:S= (其中a , b , c为三角形的三边长,p= ,S为三角形的面积).利用上述材料解决问题:当a= ,b=3,c=2 时.(1)、直接写出p的化简结果为 .(2)、写出计算S值的过程.24. 用充电器给某手机充电时,其屏幕的起始画面如图①.
(1)、求该一次函数的解析式;(2)、画出该一次函数的图象,并根据图象回答:当x取何值时,一次函数y=kx+b的函数值大于3?23. 材料:海伦公式是利用三角形三条边长求三角形面积的公式,用符号表示为:S= (其中a , b , c为三角形的三边长,p= ,S为三角形的面积).利用上述材料解决问题:当a= ,b=3,c=2 时.(1)、直接写出p的化简结果为 .(2)、写出计算S值的过程.24. 用充电器给某手机充电时,其屏幕的起始画面如图①.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量E(单位:%)与充电时间t(单位:h)的函数图象分别为图②中的线段AB、AC.
根据以上信息,回答下列问题:
(1)、在目前电量20%的情况下,用充电器给该手机充满电时,快速充电器比普通充电器少用多少小时?(2)、求线段AB、AC对应的函数表达式;(3)、已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用ah,接着再用普通充电器将其充满电,其“充电﹣耗电﹣充电”的时间恰好是6h,求a的值.25. 如图所示,已知△ABC中,∠B=90°,AB=16cm , AC=20cm , P、Q是△ABC的边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm , 点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm , 它们同时出发,设出发的时间为ts .根据以上信息,回答下面问题:
 (1)、求BC的长度;(2)、当t为何值时,点P在边AC的垂直平分线上?(3)、当点Q在边CA上运动时,是否存在t的值,使△BCQ为等腰三角形,若存在,请求出t的值;若不存在,请说明理由.
(1)、求BC的长度;(2)、当t为何值时,点P在边AC的垂直平分线上?(3)、当点Q在边CA上运动时,是否存在t的值,使△BCQ为等腰三角形,若存在,请求出t的值;若不存在,请说明理由.