安徽省阜阳市阜南县2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2021-08-23 类型：期中考试

进入出卷网下载

一、单选题

1. 点 $A (3 ， 2)$ 关于x轴的对称点为B，则点B的坐标为（）

A、 $(3 ， 2)$ B、 $(- 3 ， - 2)$ C、 $(- 3 ， 2)$ D、 $(3 ， - 2)$

查看试题解析
2. 下列长度的三条线段能组成三角形的是（）

A、2，3，1 B、4，11，6 C、5，5，5 D、4，4，8

查看试题解析
3. 函数 $y = \frac{\sqrt{1 - x}}{x}$ 中，自变量x的取值范围是（）

A、 $x \leq 1$ B、 $x \geq 1$ C、 $x<1$ 且 $x \neq 0$ D、 $x \leq 1$ 且 $x \neq 0$

查看试题解析
4. 下列命题中，假命题的是（）

A、对顶角相等 B、同位角相等 C、两点之间线段最短 D、垂线段最短

查看试题解析
5. 如图，已知一次函数y=ax-1与y=mx+4的图象交于点A(3，1)，则关于x的方ax-1=mx+4的解是（）

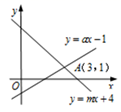A、x=-1 B、x=1 C、x=3 D、x=4 ．

查看试题解析
6. 给定下列条件，不能判定三角形是直角三角形的是（）

A、 $∠ A ： ∠ B ： ∠ C = 1 ： 2 ： 3$ B、 $∠ A - ∠ C = ∠ B$ C、 $∠ A = ∠ B = 2 ∠ C$ D、 $∠ A = ∠ B = \frac{1}{2} ∠ C$

查看试题解析
7. 已知点 $P (- 1 ， y_{1})$ 、点 $Q (3 ， y_{2})$ 在一次函数 $y = (2 m - 1) x + 2$ 的图像上，且 $y_{1} > y_{2}$ ，则m的取值范围是（）

A、 $m < \frac{1}{2}$ B、 $m > \frac{1}{2}$ C、 $m \geq 1$ D、 $m < 1$

查看试题解析
8. 如图， $△ A B C$ 中， $∠ E F D = 30 °$ 且 $∠ A E F = ∠ A F E$ ， $∠ C F D = ∠ C D F$ ，则 $∠ A B C$ 的度数（）

A、90° B、110° C、120° D、150°

查看试题解析
9. 平面直角坐标系中，过点（-2，3）的直线经过一、二、三象限，若点（0，a），（-1，b），（c，-1）都在直线l上，则下列判断正确的是（）

A、 $a < b$ B、 $a < 3$ C、 $b < 3$ D、 $c < - 2$

查看试题解析
10. 如图，一个粒子在第一象限和x，y轴的正半轴上运动，在第一秒内，它从原点运动到(0，1)，接着它按图所示在x轴、y轴的平行方向来回运动，即(0，0)→(0，1)→(1，1)→(1，0)→(2，0)→…，且每秒运动一个单位长度，那么2020秒时，这个粒子所处位置为（）

A、(4，44) B、(5，44) C、(44，4) D、(44，5)

查看试题解析

二、填空题

11. 已知y=(m-1)x^m2 -1是关于x的一次函数，则m为．

查看试题解析
12. 点A在第二象限，且到x轴的距离是4，到y轴的距离是2，则点A的坐标是．

查看试题解析
13. 已知一个等腰三角形一边长为3，周长为15，则它的腰长等于.

查看试题解析

三、解答题

14. 开学前夕，某服装厂接到为一所学校加工校服的任务，要求5天内加工完220套校服，服装厂安排甲、乙两车间共同完成加工任务，乙车间加工中途停工一段时间维修设备，然后改变加工效率继续加工，直到与甲车间同时完成加工任务为止，设甲乙两车间各自加工校服数量y套与甲车间加工时间x天之间的关系如图①所示，未加工校服w套与甲加工时间x天之间的关系如图②所示，

(1)、甲车间每天加工防护服套

(2)、求乙车间维修设备后，乙车间加工防护服数量y（套）和x（天）之间的函数关系式

查看试题解析
15. 如图，将三角形ABC向右平移3个单位长度，再向下平移2个单位长度，得到对应的三角形A₁B₁C₁.

(1)、画出三角形A₁B₁C₁并写出点A₁、B₁、C₁的坐标.

(2)、求三角形A₁B₁C₁的面积.

查看试题解析
16. 如图，有三个论断① $∠ 1 = ∠ 2$ ；② $∠ B = ∠ D$ ；③ $∠ A = ∠ C$ ，请从中任选两个作为条件，另一个作为结论构成一个命题，并证明该命题的正确性．

查看试题解析
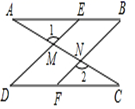17. 已知直线m的解析式 $y = 2 x + 3$ ，直线n的解析式为 $y = k x - 1 (k \neq 0)$ ，两直线交于点A，A点的横坐标为 $- 1$ ，求A点的坐标和直线n的解析式．

查看试题解析
18. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝36°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E ．

(1)、求∠CBE的度数；

(2)、点F是AE延长线上一点，过点F作∠AFD＝27°，交AB的延长线于点D ．求证：BE∥DF ．

查看试题解析
19. 已知直线经过 $(2 ， 5)$ ， $(- 6 ， - 7)$ 两点．

(1)、求直线的函数解析式；

(2)、若直线与x轴交于点A，与y轴交于点B．过B点作直线BP与x轴交于点P，且使 $O P = 2 O A$ ，求 $△ A B P$ 的面积．

查看试题解析
20. 如图，AD为△ABC的中线，BE为△ABD的中线.

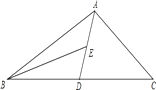(1)、在△BED中作BD边上的高EF.

(2)、若△ABC的面积为60，BD=5，求EF的长.

查看试题解析
21. 如图，在直角坐标系中，直线 $l_{1} ： y = k x - 1$ 与直线 $l_{2} ； y = \frac{1}{2} x + 2$ 交于点 $A (m ， 1)$ ．

(1)、求m的值．

(2)、设直线 $l_{1}$ ， $l_{2}$ ，分别于y轴交于点B，C，求 $△ A B C$ 的面积．

(3)、结合图像，直接写出不等式 $0 < k x - 1 < \frac{1}{2} x + 2$ 的解集．

查看试题解析
22. 为了做好新冠的个人防疫，小明妈妈联合班级其他同学的家长去药店团购口罩，口罩原来一包是20元，由于家长们购买的数量比较多，药店老板决定给他们优惠，方式如下：
方式一：每包口罩打九折；

方式二：如果购买的口罩不超过40包，则口罩按原价销售，如果购买的口罩超过40包，则超出的部分打八折销售．设大家一共需要团购口罩x包，

(1)、口罩的总费用为y元，请分别求出两种方式y与x的关系式；

(2)、已知每位家长为孩子都准备5包口罩，小明妈妈根据联合家长的人数如何选择优惠方式？

查看试题解析
23. 在 $△ A B C$ 中， $∠ C = 80 °$ ，点D、E分别是 $△ A B C$ 边AC、BC（不与A、B、C重合）上的点，（P与D、E不在同一条战线上），令 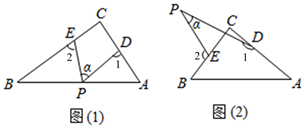$∠ P D A = ∠ 1$ ， $∠ P E B = ∠ 2$ ， $∠ D P E = ∠ α$ ．

(1)、若点P在边AB上，如图（1）且 $∠ α = 40 °$ ，则 $∠ 1 + ∠ 2 =$ °；

(2)、若点P在 $△ A B C$ 的外部如图（2）则 $∠ α$ ， $∠ 1$ ， $∠ 2$ 之间有何关系？

(3)、若点P在 $△ A B C$ 边BA的延长线上运动（ $C D > C E$ ），直接写出 $∠ α$ ， $∠ 1$ ， $∠ 2$ 之间的关系．

查看试题解析