天津市河东区2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-23 类型：期末考试

进入出卷网下载

一、单选题

1. 某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为100、200、300、400件，为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丁种型号的产品中抽取（）件.

A、24 B、18 C、12 D、6

查看试题解析
2. 下列事件中，随机事件的个数是（）
①2022年8月18日，北京市不下雨；②在标准大气压下，水在4℃时结冰；③从标有1，2，3，4的4张号签中任取一张，恰为1号签；④ $x \in R$ ，则 $| x |$ 的值不小于0．

A、1 B、2 C、3 D、4

查看试题解析
3. 已知m，n是两条不同直线，α，β是两个不同平面，则下列命题正确的是（　　）

A、若α，β垂直于同一平面，则α与β平行 B、若m，n平行于同一平面，则m与n平行 C、若α，β不平行，则在α内不存在与β平行的直线 D、若m，n不平行，则m与n不可能垂直于同一平面

查看试题解析
4. 如图，在三棱锥 $P - A B C$ 中， $P A ⊥$ 平面 $A B C$ ， $∠ B A C = 90 °$ ，则二面角 $B - A C - P$ 的平面角是（）

A、90° B、60° C、45° D、30°

查看试题解析
5. 在5盒酸奶中，有2盒已经过了保质期，从中任取2盒，取到的酸奶中有已过保质期的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{7}{10}$ D、 $\frac{1}{5}$

查看试题解析
6. 如图是某公司2018年1月至12月空调销售任务及完成情况的统计图，如10月份销售任务是400台，完成率为90%，下列叙述不正确的是（）

A、2018年3月的销售任务是400台 B、2018年月销售任务的平均值不超过600台 C、2018年总销售量为4870台 D、2018年月销售量最大的是6月份

查看试题解析
7. 在空间四边形ABCD中，AB＝BC，AD＝CD，E为对角线AC的中点，下列判断正确的是（）

A、平面ABC⊥平面BED B、平面ABC⊥平面ABD C、平面ABC⊥平面ADC D、平面ABD⊥平面BDC

查看试题解析
8. 三棱锥 $S - A B C$ 中， $S A ⊥$ 底面ABC， $S A = 4$ ， $A B = 3$ ，D为AB的中点， $∠ A B C = 90 °$ ，则点D到面 $S B C$ 的距离等于（）

A、 $\frac{12}{5}$ B、 $\frac{9}{5}$ C、 $\frac{6}{5}$ D、 $\frac{3}{5}$

查看试题解析

二、填空题

9. 某次能力测试中，10人的成绩统计如表，则这10人成绩的20%分位数为．

分数

5

4

3

2

1

人数（单位：人）

3

1

2

1

3

查看试题解析
10. 掷两颗骰子，出现点数之和等于8的概率等于．

查看试题解析
11. 如图， $α \cap β = C D$ ， $α \cap γ = E F$ ， $β \cap γ = A B$ ， $A B // α$ ，则CD与EF的位置关系为．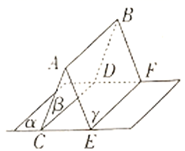

查看试题解析
12. $A ， B ， C ， D$ 四名学生按任意次序站成一排，则 $A$ 或 $B$ 在边上的概率为.

查看试题解析
13.
为了解本市居民的生活成本，甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查．他们将调查所得到的数据分别绘制成频率分布直方图（如图所示），记甲、乙、丙所调查数据的标准差分别为s₁ ， s₂ ， s₃ ，则它们的大小关系为（用“＞”连接）

查看试题解析
14. 如图，正方体 $A B C D A_{1} B_{1} C_{1} D_{1}$ 的棱长为1，线段 $B_{1} D_{1}$ 上有两个动点 $E$ ， $F$ ，且 $E F = \frac{\sqrt{2}}{2}$ ，现有下列结论：① $A C ⊥ B E$ ；②平面 $A E F$ 与平面 $A B C D$ 的交线平行于直线 $E F$ ；③异面直线 $A E$ ， $B F$ 所成的角为定值；④三棱锥 $A - B E F$ 的体积为定值，其中错误结论的是．

查看试题解析

三、解答题

15. 如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C = 9$ ， $B C = 12$ ， $A B = 15$ ，点 $D$ 是 $A B$ 的中点.

(1)、求证： $A C ⊥ B_{1} C$ ；

(2)、求证： $A C_{1} //$ 平面 $C D B_{1}$ .

查看试题解析
16. 据平安保险公司统计，某地车主购买车损险的概率为0.5，购买第三者人身安全险的概率为0.6．购买两种保险相互独立，各车主间相互独立．
①求一位车主同时购买车损险与第三者人身安全险保险的概率．

②求一位车主购买第三者人身安全险但不购买车损险的概率．

查看试题解析
17. 某校高一举行了一次数学竞赛，为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100）作为样本（样本容量n）进行统计，按照 $[50 ， 60)$ 、 $[60 ， 70)$ 、 $[70 ， 80)$ 、 $[80 ， 90)$ 、 $[90 ， 100]$ 的分组作出频率分布直方图，已知得分在 $[50 ， 60)$ 、 $[90 ， 100]$ 的频数分别为8、2.

(1)、求样本容量n和频率分布直方图中的x、y的值；

(2)、估计本次竞赛学生成绩的众数、中位数、平均数.

查看试题解析
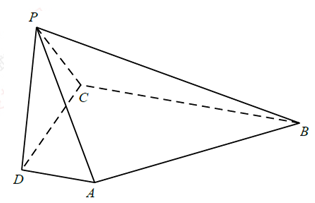
18. 某市规定，高中学生在校期间须参加不少于80小时的社区服务才合格．某校随机抽取20位学生参加社区服务的数据，按时间段[75，80），[80，85），[85，90），[90，95），[95，100]（单位：小时）进行统计，其频率分布直方图如图所示．

(1)、求抽取的20人中，参加社区服务时间不少于90小时的学生人数；

(2)、从参加社区服务时间不少于90小时的学生中任意选取2人，求所选学生的参加社区服务时间在同一时间段内的概率．

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中， $A D ⊥$ 平面 $P D C$ ， $A D ∥ B C$ ， $P D ⊥ P B$ ， $A D = 1$ ， $B C = 3$ ， $C D = 4$ ， $P D = 2$ .
（I）求异面直线 $A P$ 与 $B C$ 所成角的余弦值；

（II）求证： $P D ⊥$ 平面 $P B C$ ；

（Ⅲ）求直线 $A B$ 与平面 $P B C$ 所成角的正弦值.

查看试题解析

分数	5	4	3	2	1
人数（单位：人）	3	1	2	1	3