福建省三明市2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-23 类型：期末考试

进入出卷网下载

一、单选题

1. 青少年近视问题已经成为我国面临的重要社会问题.现用分层随机抽样的方法调查某校学生的视力情况，该校三个年级的学生人数如下表：

年级

高一

高二

高三

人数

550

500

450

已知在抽取的样本中，高二年级有20人，那么该样本中高三年级的人数为（）

A、18 B、20 C、22 D、24

查看试题解析
2. 用斜二测画法画水平放置的 $△ A B C$ 的直观图 $△ A^{'} B^{'} C^{'}$ 如图所示，则在 $△ A B C$ 的三边及中线AD中，最长的线段是（）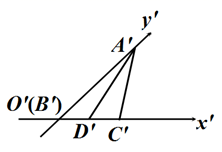

A、AB B、AD C、BC D、AC

查看试题解析
3. 下列结论正确的是(　　)

A、对事件A的概率P(A)必有0<P(A)<1 B、若事件A的概率P(A)=0.999，则事件A是必然事件 C、用某种药物对患有胃溃疡的500名病人治疗，结果有380人有明显的疗效，现有胃溃疡的病人服用此药，则估计其会有明显疗效可能性为76% D、某奖券中奖率为50%，则某人购买此奖券10张，一定有5张中奖

查看试题解析
4. 若某同学连续3次考试的名次（3次考试均没有出现并列名次的情况）不低于第3名，则称该同学为班级的尖子生.根据甲、乙、丙、丁四位同学过去连续3次考试名次的数据，推断一定是尖子生的是（）

A、甲同学：平均数为2，方差小于1 B、乙同学：平均数为2，众数为1 C、丙同学：中位数为2，众数为2 D、丁同学：众数为2，方差大于1

查看试题解析
5. 设D，E分别为 $△ A B C$ 两边 $B C$ ， $C A$ 的中点，则 $\vec{A D} + \vec{E B} =$ （）

A、 $\frac{1}{2} \vec{A C}$ B、 $\frac{3}{2} \vec{A C}$ C、 $\frac{1}{2} \vec{A B}$ D、 $\frac{3}{2} \vec{A B}$

查看试题解析
6. 袋子中有大小、形状、质地完全相同的4个小球，分别写有“风”、“展”、“红”、“旗”四个字，若有放回地从袋子中任意摸出一个小球，直到写有“红”、“旗”的两个球都摸到就停止摸球.利用电脑随机产生1到4之间取整数值的随机数，用1，2，3，4分别代表“风”、“展”、“红”、“旗”这四个字，以每三个随机数为一组，表示摸球三次的结果，经随机模拟产生了以下20组随机数：
411   231   324   412   112   443   213   144   331   123

114   142   111   344   312   334   223   122   113   133

由此可以估计，恰好在第三次就停止摸球的概率为（    ）

A、 $\frac{1}{10}$ B、 $\frac{3}{20}$ C、 $\frac{1}{5}$ D、 $\frac{1}{4}$

查看试题解析
7. 如图，在三棱锥P—ABC中，点D，E分别为棱PB，BC的中点.若点F在线段AC上，且满足AD $/ /$ 平面PEF，则 $\frac{A F}{F C}$ 的值为（）

A、1 B、2 C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
8. $△ A B C$ 中，若 $A B = A C = 5$ ， $B C = 6$ ，点 $E$ 满足 $\vec{C E} = \frac{2}{15} \vec{C A} + \frac{1}{5} \vec{C B}$ ，直线 $C E$ 与直线 $A B$ 相交于点 $D$ ，则 $\cos ∠ A D E =$ （）

A、 $\frac{\sqrt{10}}{10}$ B、 $\frac{3 \sqrt{10}}{10}$ C、 $- \frac{\sqrt{10}}{10}$ D、 $- \frac{3 \sqrt{10}}{10}$

查看试题解析

二、多选题

9. 从1至9这9个自然数中任取两个，有如下随机事件：
A=“恰有一个偶数”，B=“恰有一个奇数”，

C=“至少有一个是奇数”，D=“两个数都是偶数”，

E=“至多有一个奇数”.

下列结论正确的有（）

A、 $A = B$ B、 $B \subseteq C$ C、 $D \cap E = \emptyset$ D、 $C \cap D = \emptyset$ ， $C \cup D = Ω$

查看试题解析
10. 下列命题正确的是（）

A、若 $\vec{a} \cdot \vec{b} = 0$ ，则 $\vec{a} = 0$ 或 $\vec{b} = 0$ B、已知 $\vec{a} = (3 ， 4)$ ， $\vec{b} = (0 ， 1)$ ，则向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量的坐标为 $(0 ， 4)$ C、若 $\vec{a} \cdot \vec{b} < 0$ ，则向量 $\vec{a}$ ， $\vec{b}$ 的夹角为钝角 D、设 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 是同一平面内两个不共线的向量，则 $\vec{a} = 2 \vec{e_{1}} + \vec{e_{2}}$ ， $\vec{b} = \vec{e_{1}} + 2 \vec{e_{2}}$ 可作为该平面的一个基底

查看试题解析
11. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $E$ 、 $F$ 分别是棱 $C_{1} D_{1}$ 、 $A_{1} D_{1}$ 上的动点.、给出下面四个命题，其中正确的是（）

A、 $E F // A C$ B、直线 $A F$ 与直线 $C E$ 所成角的最大值是 $\frac{π}{3}$ C、若直线 $A F$ 与直线 $C E$ 相交，则交点在直线 $D D_{1}$ 上 D、若直线 $A F$ 与直线 $C E$ 相交，则二面角 $E - A C - D$ 的平面角的最小正切值为 $\sqrt{2}$

查看试题解析
12. 在△ $A B C$ 中， $∠ A B C = 90 °$ ， $A B = \sqrt{3}$ ， $B C = 1$ ，P为△ $A B C$ 内一点， $∠ B P C = 90 °$ ，下列结论正确的是（）

A、若 $P B = \frac{1}{2}$ ，则 $P A = \frac{\sqrt{13}}{2}$ B、若 $∠ A P B = 150 °$ ，则 $\frac{P B}{P C} = \frac{\sqrt{3}}{4}$ C、△ $B P C$ 的面积的最大值为 $\frac{1}{4}$ D、△ $A B P$ 的面积的取值范围是 $(0 ， \frac{3 \sqrt{3}}{8}]$

查看试题解析

三、填空题

13. 设 $a \in R$ ，若复数 $z = (a^{2} - 4) + (a + 2) i$ 是纯虚数，则 $a =$ .

查看试题解析
14. 2021年1月1日起，三明市全面铺开市区生活垃圾分类工作，生活垃圾需按照“可回收物”、“有害垃圾”、“厨余垃圾”、“其他垃圾”的标准进行分类投放.若某居民将“厨余垃圾“和“可回收物“两袋垃圾随机地投放到四个分类垃圾桶中的两个，则两袋垃圾均投放准确的概率为.

查看试题解析
15. 已知正三棱锥 $A - B C D$ 的底面是边长为3的正三角形，其外接球O的表面积为 $16 π$ ，且点A到底面 $B C D$ 的距离小于外接球O的半径，E为 $A D$ 的中点，则异面直线 $A B$ 与 $C E$ 所成角的余弦值为.

查看试题解析
16. “阿基米德多面体”也称为半正多面体，是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.如图，是一个棱长为1的半正多面体，它的所有顶点都在同一个正方体的表面上.则该正方体的棱长为；半正多面体的表面积为.

查看试题解析

四、解答题

17. 在复平面内，O为坐标原点，复数 $z_{1} = \sqrt{3} + i$ ， $z_{2} = 1 + \sqrt{3} i$ 所对应的向量分别为 $\vec{O A}$ ， $\vec{O B}$ .

(1)、求 $\frac{z_{2}}{z_{1}}$ 所对应的点C的坐标；

(2)、求 $\frac{S_{△ A O B}}{S_{△ B O C}}$ 的值

查看试题解析
18. 三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧面 $B C C_{1} B_{1}$ 是边长为 $\sqrt{3}$ 的菱形， $A_{1} C_{1} = B_{1} C = 2$ ， $A_{1} B_{1} ⊥$ 平面 $B C C_{1} B_{1}$ ，E，F分别是 $A C$ ， $B B_{1}$ 的中点.

(1)、求证： $E F //$ 平面 $A_{1} B_{1} C$ ；

(2)、求直线 $A_{1} C_{1}$ 与平面 $A_{1} B_{1} C$ 所成的角.

查看试题解析
19. 在 $△ A B C$ 中，角A，B，C的对边分别为a，b，c，且 $a = b (\sin C + \cos C)$ .

(1)、求B；

(2)、若 $a = 1$ ， $C = \frac{π}{6}$ ，求 $△ A B C$ 的面积.

查看试题解析
20. 为庆祝中国共产党成立100周年，某校举行了党史知识竞赛，在必答题环节，甲、乙两位选手分别从3道选择题、2道填空题中随机抽取2道题作答，若甲每道题答对的概率为 $\frac{2}{3}$ ，乙每道题答对的概率为 $\frac{3}{4}$ ，且甲乙答对与否互不影响，各题的结果也互不影响.求：

(1)、甲至少抽到1道填空题的概率；

(2)、甲答对的题数比乙多的概率.

查看试题解析
21. 已知A，B两家公司的员工月均工资情况如下：

(1)、以每组数据的区间中点值代表该组数据的平均水平，根据图1估计A公司员工月均工资的平均数、中位数，你认为用哪个数据更能反映该公司普通员工的工资水平？请简要说明理由.

(2)、小明拟到A，B两家公司中的一家应聘，以公司普通员工的工资水平作为决策依据，他应该选哪个公司？

查看试题解析
22. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是菱形， $∠ B A D = 60 °$ ， $△ P A D$ 是正三角形，E为线段 $A D$ 的中点， $\vec{P F} = λ \vec{F C} (λ > 0)$ .

(1)、求证：平面 $P B C ⊥$ 平面 $P B E$ ；

(2)、是否存在点F，使得 $V_{B - P A E} = \frac{5}{8} V_{D - P F B}$ ？若存在，求出 $λ$ 的值；若不存在，请说明理由.

(3)、若平面 $P A D ⊥$ 平面 $A B C D$ ，在平面 $P B E$ 内确定一点H，使 $C H + F H$ 的值最小，并求此时 $\frac{B H}{B P}$ 的值.

查看试题解析

年级	高一	高二	高三
人数	550	500	450