福建省宁德市2020-2021学年高一下学期数学期末试卷

试卷更新日期：2021-08-23 类型：期末考试

进入出卷网下载

一、单选题

1. 已知复数z满足 $z = i (1 + i)$ ，则 $\overline{z}$ 是（）

A、－1＋i B、－1－i C、1＋i D、1－i

查看试题解析
2. 掷两枚质地均匀的骰子，记事件A＝“第一枚出现奇数点”，事件B＝“第二枚出现偶数点”，则事件A与事件B的关系为（）

A、A与B互斥 B、A与B对立 C、A与B独立 D、A与B相等

查看试题解析
3. 如图①、②分别是甲、乙两户居民家庭全年各项支出的统计图.根据统计图，下列对两户教育支出占全年总支出的百分比作出的判断中，正确的是（）

A、甲户比乙户大 B、乙户比甲户大 C、甲、乙两户一般大 D、无法确定哪一户大

查看试题解析
4. 如图是正方体的平面展开图，则在这个正方体中， $A M$ 与 $B N$ 所成角的大小为（）

A、 $0^{\circ}$ B、 $90^{\circ}$ C、 $60^{\circ}$ D、 $45^{\circ}$

查看试题解析
5. 已知 $m$ ， $n$ 是两条直线， $α$ ， $β$ 是两个平面，下列说法正确的是（）

A、若 $m / / n$ ， $n / / α$ ，则 $m / / α$ B、若 $α ⊥ β$ ， $m \subset α$ ，则 $m ⊥ β$ C、若 $m / / α$ ， $n \subset α$ ，则 $m / / n$ D、若 $m \subset α$ ， $m ⊥ β$ ，则 $α ⊥ β$

查看试题解析
6. 已知某运动员每次投篮命中的概率是40%．现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器产生0到9之间取整数值的随机数，指定1，2，3，4表示命中，5，6，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果．经随机模拟产生了如下10组随机数：204 978 171 935 263 321 947 468 579 682，据此估计，该运动员三次投篮恰有两次命中的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{3}{10}$ C、 $\frac{2}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 《史记》中讲述了田忌与齐王赛马的故事，其中，田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马；田忌的下等马劣于齐王的下等马，若双方各自拥有上等马、中等马、下等马各1匹，且双方各自随机选1匹马进行1场比赛，则田忌的马获胜的概率为（）

A、 $\frac{5}{6}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
8. 如图，由四个全等的直角三角形与一个小正方形拼成的一个大正方形，已知 $\vec{A B} = \vec{a} ， \vec{A D} = \vec{b} ， \vec{A F} = 2 \vec{F E}$ ，则 $\vec{A E} =$ （）

A、 $\frac{3}{4} \vec{a} + \frac{1}{2} \vec{b}$ B、 $\frac{12}{25} \vec{a} + \frac{16}{25} \vec{b}$ C、 $\frac{6}{13} \vec{a} + \frac{9}{13} \vec{b}$ D、 $\frac{2}{7} \vec{a} + \frac{3}{7} \vec{b}$

查看试题解析

二、多选题

9. 设向量 $\vec{a} = (1 ， - 1) ， \vec{b} = (2 ， 0)$ ，则（）

A、 $| \vec{a} - \vec{b} | = | \vec{a} |$ B、 $(\vec{a} - \vec{b}) / / \vec{a}$ C、 $(\vec{a} - \vec{b}) ⊥ \vec{a}$ D、 $\vec{a}$ 在 $\vec{b}$ 上的投影向量为（1，0）

查看试题解析
10. 任何一个复数z＝a＋b $i$ （其中a、b∈R， $i$ 为虚数单位）都可以表示成： $z = r (\cos θ + i \sin θ)$ 的形式，通常称之为复数z的三角形式．法国数学家棣莫弗发现： $z^{n} = {[r (\cos θ + i \sin θ)]}^{n} = r^{n} (\cos n θ + i \sin n θ) (n \in N_{+})$ ，我们称这个结论为棣莫弗定理．根据以上信息，下列说法正确的是（）

A、当 $r = 1 ， θ = \frac{π}{3} ， n = 1$ 时， $\bar{z} = \frac{1}{2} - \frac{\sqrt{3}}{2} i$ B、 ${(\frac{1}{2} + \frac{\sqrt{3}}{2} i)}^{3} = 1$ C、 $| z^{4} | = | z |^{4}$ D、 ${(\frac{\sqrt{3}}{2} + \frac{1}{2} i)}^{10}$ 在复平面内对应的点的坐标在第三象限

查看试题解析
11. 已知正四面体的外接球、内切球的球面上各有一动点M、N，若线段MN的最小值为 $2 \sqrt{6}$ ，则（）

A、正四面体的外接球的表面积为 $96 π$ B、正四面体的内切球的体积为 $8 \sqrt{6} π$ C、正四面体的棱长为12 D、线段MN的最大值为 $3 \sqrt{6}$

查看试题解析
12. 新冠肺炎期间，某社区规定：若任意连续7天，每天不超过6人体温高于37.3℃，则称没有发生群体性发热．下列连续7天体温高于37.3℃人数的统计特征数中，能判定该社区没有发生群体性发热的为（）

A、中位数为4，众数为3 B、均值小于1，中位数为1 C、均值为2，标准差为 $\sqrt{3}$ D、均值为3，众数为4

查看试题解析

三、填空题

13. 已知 $z = \frac{1 + 2 i}{1 - 2 i}$ ，则 $| z | =$ ．

查看试题解析
14. 在△ABC中，若b = 1，c = $\sqrt{3}$ ， $∠ C = \frac{2 π}{3}$ ，则a =

查看试题解析
15. 如图，桌面上放置一个装有水的圆柱形玻璃水杯，AB为杯底直径，现以点B为支点将水杯倾斜，使AB所在直线与桌面所成的角为 $\frac{π}{6}$ ，则圆柱母线与水面所在平面所成的角等于．

查看试题解析
16. 菱形ABCD的边长为2，∠A＝60°，M为DC的中点，若N为菱形内任意一点（含边界），则 $\vec{A M} \cdot \vec{B N}$ 的最小值为．

查看试题解析

四、解答题

17. 已知向量 $\vec{a} ， \vec{b}$ 满足 $\vec{a} = (1 ， 1) ， | \vec{b} | = 1$ ．

(1)、若 $\vec{a} ， \vec{b}$ 的夹角 $θ$ 为 $\frac{π}{4}$ ，求 $\vec{a} \cdot \vec{b}$ ；

(2)、若 $(\vec{a} + \vec{b}) ⊥ \vec{b}$ ，求 $\vec{a}$ 与 $\vec{b}$ 的夹角．

查看试题解析
18. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B$ ⊥ $A C$ ，AB＝AC＝1，D是BC的中点．

(1)、求证： $A_{1} B$ //平面 $A D C_{1}$ ；

(2)、若面 $A B B_{1} A_{1}$ ⊥面ABC， $A A_{1} ⊥ A B ， A A_{1} = 2$ ，求几何体 $A B D - A_{1} B_{1} C_{1}$ 的体积．

查看试题解析
19. 某公司生产某种产品，从生产的正品中随机抽取1000件，测得产品质量差（质量差＝生产的产品质量－标准质量，单位mg）的样本数据统计如下：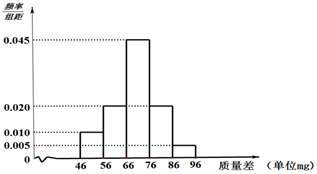

(1)、求样本数据的80%分位数；

(2)、公司从生产的正品中按产品质量差进行分拣，若质量差在 $(\bar{x} - s ， \bar{x} + s)$ 范围内的产品为一等品，其余为二等品．其中 $\bar{x} ， s$ 分别为样本平均数和样本标准差，计算可得s≈10（同一组中的数据用该组区间的中点值作代表）．
①若产品的质量差为62mg，试判断该产品是否属于一等品；

②假如公司包装时要求，3件一等品和2件二等品装在同一个箱子中，质检员每次从箱子中摸出2件产品进行检验，求摸出2件产品中至少有1件一等品的概率．

查看试题解析
20. 现给出两个条件：① $2 b \sin A = a \tan B$ ，② $a (\sin A - \sin C) = b \sin B - c \sin C$ ，从中选出一个条件补充在下面的问题中，并以此为依据求解问题．
在△ABC中，a，b，c分别为内角A，B，C所对的边，若．

(1)、求B；

(2)、若点D是边AC靠近A的三等分点，且BD长为1，求△ABC面积的最大值．

查看试题解析
21. 甲、乙、丙三人参加一家公司的招聘面试，面试合格者可正式签约．甲表示只要面试合格就签约，乙丙则约定：两人面试都合格就一同签约，否则两人都不签约．设甲面试合格的概率为 $\frac{1}{3}$ ，乙丙每人面试合格的概率都是 $\frac{1}{4}$ ，且三人面试是否合格互不影响．
求：

(1)、恰有一人面试合格的概率；

(2)、至多一人签约的概率．

查看试题解析
22. 在我国古代数学名著《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”．已知三棱锥P－ABC中，PA⊥平面ABC．

(1)、从三棱锥P－ABC中选择合适的两条棱填空．若 ▲ ⊥ ▲ ，则该三棱锥为“鳖臑”；

(2)、已知三棱锥P－ABC是一个“鳖臑”，且AC＝1，AB＝2，∠BAC＝60°.
①若△PAC上有一点D，如图1所示，试在平面PAC内作出一条过点D的直线l，使得l与BD垂直，说明作法，并给予证明；

②若点D在线段PC上，点E在线段PB上，如图2所示，且PB⊥平面EDA，证明∠EAB是平面EAD与平面BAC的二面角的平面角．

查看试题解析