北京市丰台区2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-23 类型：期末考试

进入出卷网下载

一、单选题

1. 在复平面内，复数 $z = 1 - i$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知向量 $\vec{a} = (1 ， 3)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则向量 $\vec{b}$ 可以是（）

A、 $(- 3 ， 1)$ B、 $(- 3 ， - 1)$ C、 $(3 ， 1)$ D、 $(- 1 ， - 3)$

查看试题解析
3. 在平行四边形ABCD中， $O$ 是对角线AC和BD的交点，则 $\vec{A O} + \vec{O D} - \vec{D C} =$ （）

A、 $\vec{A C}$ B、 $\vec{C A}$ C、 $\vec{B D}$ D、 $\vec{D B}$

查看试题解析
4. 已知正三棱锥 $P - A B C$ ，底面 $A B C$ 的中心为点 $O$ ，给出下列结论：
① $P O$ $⊥$ 底面 $A B C$ ；

②棱长都相等；

③侧面是全等的等腰三角形．

其中所有正确结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
5. 已知 $\sin x = \frac{1}{3}$ ，则 $\cos 2 x =$ （）

A、 $\frac{8}{9}$ B、 $\frac{7}{9}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
6. 已知 $a ， b$ 是两条不同的直线， $α ， β$ 是两个不同的平面，下列命题正确的是（）

A、若 $a / / α ， b / / α$ ，则 $a / / b$ B、若 $a / / α ， a / / β$ ，则 $α / / β$ C、若 $a ⊥ α ， b ⊥ α$ ，则 $a / / b$ D、若 $a ⊥ α ， b ⊥ β$ ，则 $α / / β$

查看试题解析
7. 如图，该球O与圆柱 $O_{1} O_{2}$ 的上､下底面及母线均相切．若球O的体积为 $\frac{4 π}{3}$ ，则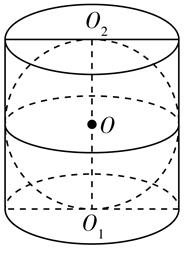圆柱 $O_{1} O_{2}$ 的表面积为（）

A、4π B、5π C、6π D、7π

查看试题解析
8. 在 $△ A B C$ 中，点 $D$ 在线段 $B C$ 上，且 $B D ＝ 3 D C$ ，若 $\vec{A D} = m \vec{A B} + n \vec{A C}$ ，则 $\frac{n}{m} =$ （）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、2 D、3

查看试题解析
9. 在 $△ A B C$ 中，若 $b = 2 a \cos C$ ，且 $B = \frac{π}{2}$ ，则 $A =$ （）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析

10. 从出生之日起，人的体力､情绪､智力呈周期性变化，在前30天内，它们的变化规律如下图所示(均为正弦型曲线)：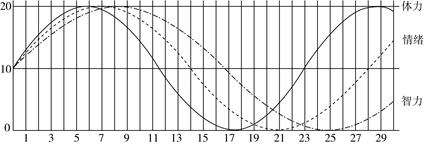

体力､情绪､智力在从出生之日起的每个周期中又存在着高潮期(前半个周期)和低潮期(后半个周期)．它们在一个周期内的表现如下表所示：

	高潮期	低潮期
体力	体力充沛	疲倦乏力
情绪	心情愉快	心情烦躁
智力	思维敏捷	反应迟钝

如果从同学甲出生到今日的天数为5850，那么今日同学甲（）

A、体力充沛，心情烦躁，思维敏捷 B、体力充沛，心情愉快，思维敏捷 C、疲倦乏力，心情愉快，思维敏捷 D、疲倦乏力，心情烦躁，反应迟钝

查看试题解析

二、填空题

11. 已知 $\vec{a} = (2 ， 3)$ ， $\vec{b} = (4 ， x)$ ，且 $\vec{a} / / \vec{b}$ ，则 $x =$ .

查看试题解析
12. 已知复数 $z = \frac{2 i}{1 + i}$ （ $i$ 为虚数单位），则 $| z | =$ ．

查看试题解析
13. 将函数 $f (x) = \cos 2 x$ 的图象向左平移 $φ (φ > 0)$ 个单位长度，得到函数 $g (x)$ 的图象．若函数 $g (x)$ 的图象关于原点对称，则 $φ$ 的一个取值为．

查看试题解析
14. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2，点 $O$ 为底面 $A B C D$ 的中心，点 $P$ 在侧面 $B B_{1} C_{1} C$ 的边界及其内部运动，且 $D_{1} O ⊥ O P$ ．给出下列结论：

① $A C ⊥ D_{1} O$ ；

②三棱锥 $P - A A_{1} D$ 的体积为定值；

③点P在线段CE上(E为BB₁的中点)；

④ $△ D_{1} C_{1} P$ 面积的最大值为2．

其中所有正确结论的序号是．

查看试题解析

15. 为调研某校学生的课外阅读情况，通过随机抽样调查，获得100名学生每天的课外阅读时间，所得数据均在区间

[50 ， 100]

(单位：

min

)上，其频率分布表如下：

分组	频率
[50，60]	0.05
(60，70]	0.35
(70，80]	$a$
(80，90]	0.2
(90，100]	0.1

则 $a =$ ；根据以上数据，估计该校学生每天课外阅读时间的80%分位数为．

查看试题解析

三、解答题

16. 已知向量 $\vec{a} = (- 1 ， 3) ， \vec{b} = (1 ， 2)$ ．

(1)、求 $\vec{a} \cdot \vec{b}$ ；

(2)、求 $\vec{a}$ 与 $\vec{b}$ 夹角的大小；

(3)、求 $| 2 \vec{a} - \vec{b} |$ ．

查看试题解析
17. BMI(身体质量指数)是目前国际上常用的衡量人体胖瘦程度以及是否健康的一个标准，其计算公式是： $B M I = \frac{体重（单位： k g ）}{身高^{2} （单位： m^{2} ）}$ ．在我国，成人的 $B M I$ 数值参考标准为： $B M I < 18.5$ 为偏瘦； $18.5 \leq B M I < 24$ 为正常； $24 \leq B M I < 28$ 为偏胖； $B M I \geq 28$ 为肥胖．某公司有3000名员工，为了解该公司员工的身体肥胖情况，研究人员从公司员工体检数据中，采用比例分配的分层随机抽样的方法抽取了100名男员工､50名女员工的身高体重数据，计算得到他们的BMI，进而得到频率分布直方图如下：

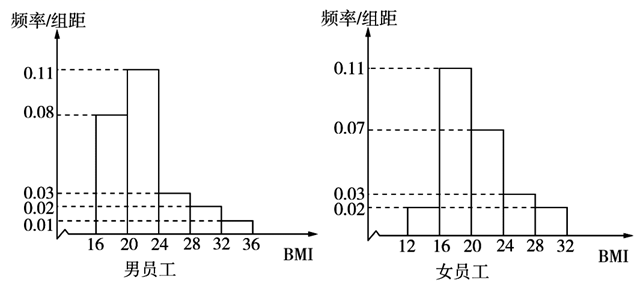(1)、该公司男员工和女员工各有多少人？

(2)、根据BMI及频率分布直方图，估计该公司男员工为肥胖的有多少人？

(3)、根据频率分布直方图，估计该公司男员工BMI的平均数为 $μ_{1}$ ，女员工BMI的平均数为 $μ_{2}$ ，比较 $μ_{1}$ 与 $μ_{2}$ 的大小．(直接写出结论，不要求证明)

查看试题解析
18. 如图，在 $△ A B C$ 中，D是BC边上一点， $\cos C = \frac{3}{5}$ ， $C D = 7$ ， $A C = 5$ ．

(1)、求AD的长；

(2)、若 $A B = 8$ ，求角B的大小

查看试题解析
19. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，侧面 $A C C_{1} A_{1} ⊥$ 底面 $A B C$ ， $B C ⊥ A C$ ．

(1)、求证： $B_{1} C_{1} / /$ 平面 $A_{1} B C$ ；

(2)、求证：平面 $A_{1} B C ⊥$ 平面 $A C C_{1} A_{1}$ ．

(3)、若 $A_{1} B = 2 B C$ ，求异面直线 $A_{1} B$ 与 $B_{1} C_{1}$ 所成角的大小．

查看试题解析
20. 已知函数 $f (x) = 2 \sin (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的最小正周期为 $π$ ．

(1)、求 $ω$ 的值；

(2)、再从条件①､条件②､条件③中选择一个作为已知条件，求函数 $g (x) = f (x) + 2 \cos 2 x$ 在区间 $[\frac{π}{2} ， π]$ 上的最小值．
条件①： $f (x)$ 的图象过点 $(\frac{π}{12} ， 0)$ ；

条件②： $f (x)$ 的图象关于直线 $x = \frac{π}{3}$ 对称；

条件③： $f (x)$ 在区间 $[- \frac{π}{6} ， \frac{π}{3}]$ 上单调递增．

注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
21. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $P A ⊥$ 底面 $A B C D$ ， $P A = A B$ ， $E$ 为线段 $P B$ 的中点， $F$ 为线段 $B C$ 上的动点．

(1)、若平面 $A D E$ 交 $P C$ 于点 $G$ ，求证： $E G / / A D$ ；

(2)、求证： $A E ⊥$ 平面 $P B C$ ；

(3)、判断直线 $A F$ 与平面 $P B C$ 所成角的大小是否可以为 $\frac{π}{3}$ ，并说明理由．

查看试题解析