北京市东城区2020-2021学年高一下学期数学期末考试试卷

试卷更新日期：2021-08-23 类型：期末考试

进入出卷网下载

一、单选题

1. 已知复数 $z = - 2 + i$ ，则 $z + \bar{z} =$ （）

A、-4 B、-2 C、2i D、0

查看试题解析
2. 若 $\vec{a} ， \vec{b}$ 都是单位向量，则下列结论一定正确的是（）

A、 $\vec{a} = \vec{b}$ B、 $\vec{a} \cdot \vec{b} = 1$ C、 $\vec{a} / / \vec{b}$ D、 $| \vec{a} | = | \vec{b} |$

查看试题解析
3. 由随机函数 $R A N D$ 生成了在区间 $[0 ， 1)$ 内的随机数 $x$ ，则下列运算中能将 $x$ 对应到区间 $[a ， b)$ 的是（）

A、 $a x + b$ B、 $b x + a$ C、 $(b - a) x + a$ D、 $(b - a) x + b$

查看试题解析
4. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 各条棱所在的直线中，与直线 $B C_{1}$ 异面且垂直的可以是（）

A、 $A A_{1}$ B、BC C、 $A_{1} D_{1}$ D、CD

查看试题解析
5. 某校组织全体学生参加了主题为“建党百年，薪火相传”的知识竞赛，随机抽取了200名学生进行成绩统计，发现抽取的学生的成绩都在50分至100分之间，进行适当分组后（每组为左闭右开的区间），画出频率分布直方图如图所示，下列说法正确的是（）

A、直方图中x的值为0.004 B、在被抽取的学生中，成绩在区间[60，70）的学生数为10 C、估计全校学生的平均成绩不低于80分 D、估计全校学生成绩的样本数据的80%分位数约为93分

查看试题解析
6. 设向量 $\vec{a} = (\cos α ， \sin β)$ ，则“ $| \vec{a} | = 1$ ”是“ $α = β$ ”的（）

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 抛掷一颗质地均匀的骰子，有如下随机事件：
$C_{1}$ ＝“点数为 $i$ ”，其中 $i =$ 1，2，3，4， 5，6；

$D_{1}$ ＝“点数不大于2”， $D_{2}$ ＝“点数不小于2”， $D_{3}$ ＝“点数大于5”；

$E =$ “点数为奇数”， $F =$ “点数为偶数”．

下列结论正确的是（）

A、 $C_{1}$ 与 $C_{2}$ 对立 B、 $D_{1}$ 与 $D_{2}$ 互斥 C、 $D_{3} \subseteq F$ D、 $E \supseteq (D_{1} \cap D_{2})$

查看试题解析
8. 将函数 $f (x) = \sin (2 x - φ)$ 的图象向右平移 $\frac{π}{6}$ 个单位长度后，得到的图象关于y轴对称，则 $φ$ 的值可以为（）

A、 $- \frac{π}{2}$ B、 $\frac{π}{6}$ C、 $\frac{π}{3}$ D、 $\frac{π}{2}$

查看试题解析
9. 若直线 $m ⊄$ 平面 $α$ ，则下列结论一定成立的个数是（）
① $α$ 内的所有直线与m异面；

② $α$ 内存在唯一一条直线与m相交；

③ $α$ 内存在直线与m平行．

A、0 B、1 C、2 D、3

查看试题解析
10. 一条河流的两岸平行，一艘船从河岸边的A处出发到河对岸．已知船在静水中的速度 $v_{1}$ 的大小为 $| v_{1} | = 10 m / s$ ，水流速度 $v_{2}$ 的大小为 $| v_{2} | = 2 m / s$ ．设船行驶方向与水流方向的夹角为 $θ$ ，若船的航程最短，则（）

A、 $θ = \frac{π}{3}$ B、 $θ = \frac{π}{2}$ C、 $\frac{π}{2} < θ < \frac{2 π}{3}$ D、 $\frac{2 π}{3} < 0 < \frac{3 π}{4}$

查看试题解析

二、填空题

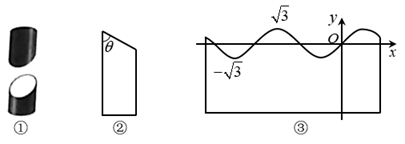
11. 在复平面内，复数 $z = {(1 + i)}^{2}$ 对应的点Z的坐标为； $| z | =$ ．

查看试题解析
12. 用一张A4纸围绕半径为rcm的石膏圆柱体包裹若干圈，然后用裁纸刀将圆柱体切为两段，如图①所示．设圆柱体母线与截面的夹角为 $θ$ （0°＜ $θ$ ＜90°），如图②．将其中一段圆柱体外包裹的A4纸展开铺平，如果忽略纸的厚度造成的误差，我们会发现剪裁边缘形成的曲线是正弦型曲线，如图③．建立适当的坐标系后，这条曲线的解析式可设为 $f (x) = A \sin ω x (A > 0 ， ω > 0)$ ，若f(x)的最小正周期为 $2 π$ ，则r＝cm，此时，当 $θ$ ＝时，可使f(x)的值域为 $[- \sqrt{3} ， \sqrt{3}]$ ．

查看试题解析
13. 已知某车企从今年开始投产了A，B，C三种型号的新能源汽车，第一个月下线的台数依次为250，450，300，现用分层抽样的方法从中随机抽取20台车进行质量测试，则某一台B型号的新能源汽车被抽取的概率为．

查看试题解析
14. 在 $△ A B C$ 中， $a^{2} = 2 b c$ ， $b = 2 c$ ， $\cos A =$ ．

查看试题解析
15. 已知⊙ $O$ 中弦 $A B = 6$ ，则 $\vec{A O} \cdot \vec{A B} =$ ．

查看试题解析
16. 已知 $α ， β$ 是平面，m是直线，从下列五个条件中选择若干个作为已知条件，能够得到 $m / / β$ 的是．（填入条件的序号即可）
① $α / / β$ ；② $α ⊥ β$ ；③ $m ⊥ α$ ；④ $m / / α$ ；⑤ $m ⊄ β$ ．

查看试题解析

三、解答题

17. 已知 $\tan α = \frac{1}{3} ， α \in (0 ， \frac{π}{2})$ ， $1 - \sin β = \cos 2 β ， β \in (\frac{π}{2} ， π)$ ．

(1)、求 $\tan (\frac{π}{4} + α)$ 及 $\sin β$ 的值；

(2)、求 $\cos (α - β)$ 的值．

查看试题解析
18. 为开学生视野，丰富学生的数学学习方式，某高校数学学院学生会创办了微信公众号《数学乐园》，设定了“数学史料”“趣题妙解”等栏目，定期发布文章．为了扩大微信公众号的影响力，后台统计了反映读者阅读情况的一些数据，其中阅读跳转率f(x)记录了在阅读某文章的所有读者中，阅读至该篇文章总量的x%时退出该页面的读者占阅读此文章所有读者的百分比．例如：阅读跳转率f（20）＝5%表示阅读某篇文章的所有读者中，阅读量至该篇文章总量的20%时退出该页面的读者占阅读此篇文章的所有读者的5%．现从“数学史料”“趣题妙解”专栏中各随机选取一篇文章．分别记为篇目A，B，其阅读跳转率的折线图如图所示．用频率来估计概率．

(1)、随机选取一名篇目A的读者，估计他退出页面时阅读量大于文章总量的80%的概率；

(2)、现用比例分配的分层随机抽样的方法，在阅读量没有达到30%的篇目B的读者中抽取6人，任选其中2人进行访谈，求这两人退出页面时阅读量都为文章总量的10%的概率；

(3)、请依据图中的数据，比较篇目A和篇目B的阅读情况，写出一个结论，并选择其中一个栏目提出你的优化建议．

查看试题解析
19. 水车是一种利用水流的动力进行灌溉的工具，工作示意图如图所示．设水车（即圆周）的直径为3米，其中心（即圆心）O到水面的距离b为1.2米，逆时针匀速旋转一圈的时间是80秒．水车边缘上一点P距水面的高度为h（单位；米），水车逆时针旋转时间为t（单位：秒）．当点P在水面上时高度记为正值；当点P旋转到水面以下时，点P距水面的高度记为负值．过点P向水面作垂线，交水面于点M，过点O作PM的垂线，交PM于点N．从水车与水面交于点Q时开始计时（t＝0），设 $∠ Q O N = φ$ ，水车逆时针旋转t秒转动的角的大小记为a．

(1)、求f(t)的函数解析式；

(2)、当雨季来临时，河流水量增加，点O到水面的距离减少了0.3米，求∠QON的大小（精确到1°）；

(3)、若水车转速加快到原来的2倍，直接写出f(t)的函数解折式．（参考数据： $\sin \frac{π}{5} \approx 0.60 ， \sin \frac{3 π}{10} \approx 0.80 ， \sin \frac{2 π}{5} \approx 0.86$ ）

查看试题解析
20. 已知点O（0，0），A（2，1），B（1，2）．

(1)、若 $\vec{O P} = \frac{1}{2} \vec{O A} + \vec{O B}$ ，求点P的坐标；

(2)、已知 $\vec{O Q} = λ \vec{O A} + μ \vec{O B}$ ．
①若点Q在直线AB：y＝－x＋3上，试写出 $λ ， μ$ 应满足的数量关系，并说明你的理由；
②若△QAB为等边三角形，求 $λ ， μ$ 的值．

查看试题解析
21. 如图①，矩形ABCD中，AB＝4，AD＝2，E，F分别为AB，DC的中点．将四边形AEFD沿EF折起至四边形 $A_{1} E F D_{1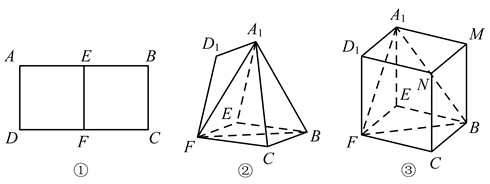}$ 的位置，如图②．

(1)、求证：EF⊥平面 $A_{1} E B$ ；

(2)、若点 $A_{1}$ 在平面EFCB上的射影为BE的中点，求三棱锥 $F - A_{1} B C$ 的体积；

(3)、当平面 $A_{1} E F D_{1}$ 与平面EFCB垂直时，作正方体 $A_{1} D_{1} N M - E F C B$ 如图③．若平面 $α$ ∥平面 $A_{1} F B$ ，且平面 $α$ 截该正方体所得图形的面积为S．
①若C∈ $α$ ，则S＝；

②S的最大值为．（直接写出结果）

查看试题解析