江西省2021年中考数学试卷
试卷更新日期:2021-08-20 类型:中考真卷
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 如图,几何体的主视图是( )
 A、
A、 B、
B、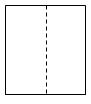 C、
C、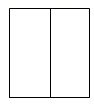 D、
D、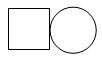 3. 计算 的结果为( )A、1 B、-1 C、 D、4. 如图是2020年中国新能源汽车购买用户地区分布图,由图可知下列说法错误的是( )
3. 计算 的结果为( )A、1 B、-1 C、 D、4. 如图是2020年中国新能源汽车购买用户地区分布图,由图可知下列说法错误的是( )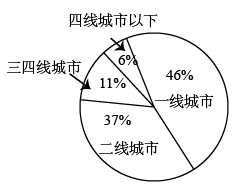 A、一线城市购买新能源汽车的用户最多 B、二线城市购买新能源汽车用户达37% C、三四线城市购买新能源汽车用户达到11万 D、四线城市以下购买新能源汽车用户最少5. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )
A、一线城市购买新能源汽车的用户最多 B、二线城市购买新能源汽车用户达37% C、三四线城市购买新能源汽车用户达到11万 D、四线城市以下购买新能源汽车用户最少5. 在同一平面直角坐标系中,二次函数 与一次函数 的图象如图所示,则二次函数 的图象可能是( )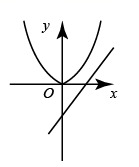 A、
A、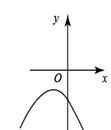 B、
B、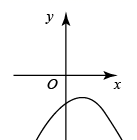 C、
C、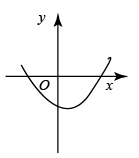 D、
D、 6. 如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )
6. 如图是用七巧板拼接成的一个轴对称图形(忽略拼接线),小亮改变①的位置,将①分别摆放在图中左,下,右的位置(摆放时无缝隙不重叠),还能拼接成不同轴对称图形的个数为( )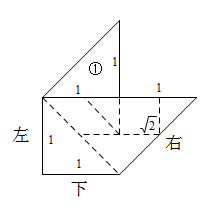 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
7. 国务院第七次全国人口普查领导小组办公室5月11日发布,江西人口数约为45100000人,将45100000用科学记数法表示为 .8. 因式分解: .9. 已知 , 是一元二次方程 的两根,则 .10. 下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过,因而人们把这个表叫做杨辉三角,请你根据杨辉三角的规律补全下表第四行空缺的数字是 .
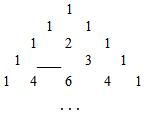 11. 如图,将 沿对角线 翻折,点 落在点 处, 交 于点 ,若 , , , ,则 的周长为 .
11. 如图,将 沿对角线 翻折,点 落在点 处, 交 于点 ,若 , , , ,则 的周长为 .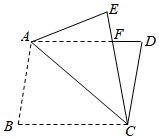 12. 如图,在边长为 的正六边形 中,连接 , ,其中点 , 分别为 和 上的动点,若以 , , 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .
12. 如图,在边长为 的正六边形 中,连接 , ,其中点 , 分别为 和 上的动点,若以 , , 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .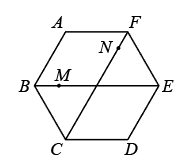
三、解答题
-
13.(1)、计算: ;(2)、如图,在 中, , , 平分 交 于点 , 于点 ,求证: .
 14. 解不等式组: ,并将解集在数轴上表示出来.
14. 解不等式组: ,并将解集在数轴上表示出来. 15. 为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从A , B , C , D四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字,(1)、“A志愿者被选中”是事件(填“随机”或“不可能”或“必然”);(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A , B两名志愿者被选中的概率.16. 已知正方形 的边长为4个单位长度,点 是 的中点,请仅用无刻度直尺按下列要求作图(保留作图痕迹).
15. 为庆祝建党100周年,某大学组织志愿者周末到社区进行党史学习宣讲,决定从A , B , C , D四名志愿者中通过抽签的方式确定两名志愿者参加.抽签规则:将四名志愿者的名字分别写在四张完全相同不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,先从中随机抽取一张卡片,记下名字,再从剩余的三张卡片中随机抽取第二张,记下名字,(1)、“A志愿者被选中”是事件(填“随机”或“不可能”或“必然”);(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果,并求出A , B两名志愿者被选中的概率.16. 已知正方形 的边长为4个单位长度,点 是 的中点,请仅用无刻度直尺按下列要求作图(保留作图痕迹).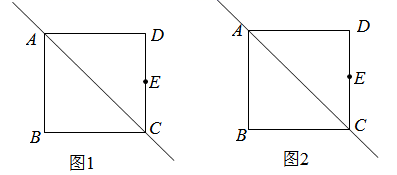 (1)、在图1中,将直线 绕着正方形 的中心顺时针旋转 ;(2)、在图2中,将直线 向上平移1个单位长度.17. 如图,正比例函数 的图象与反比例函数 ( )的图象交于点 ,在 中, , ,点 坐标为 .
(1)、在图1中,将直线 绕着正方形 的中心顺时针旋转 ;(2)、在图2中,将直线 向上平移1个单位长度.17. 如图,正比例函数 的图象与反比例函数 ( )的图象交于点 ,在 中, , ,点 坐标为 .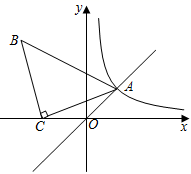 (1)、求 的值;(2)、求 所在直线的解析式.18. 甲,乙两人去市场采购相同价格的同一种商品,甲用2400元购买的商品数量比乙用3000元购买的商品数量少10件.(1)、求这种商品的单价;(2)、甲,乙两人第二次再去采购该商品时,单价比上次少了20元/件,甲购买商品的总价与上次相同,乙购买商品的数量与上次相同,则甲两次购买这种商品的平均单价是元/件,乙两次购买这种商品的平均单价是元/件.(3)、生活中,无论油价如何变化,有人总按相同金额加油,有人总按相同油量加油,结合(2)的计算结果,建议按相同加油更合算(填“金额”或“油量”).19. 为了提高农副产品的国际竞争力,我国一些行业协会对农副产品的规格进行了划分、某外贸公司要出口一批规格为 的鸡腿,现有两个厂家提供货源,它们的价格相同,鸡腿的品质相近质检员分别从两厂的产品中抽样调查了20只鸡腿,它们的质量(单位: )如下:
(1)、求 的值;(2)、求 所在直线的解析式.18. 甲,乙两人去市场采购相同价格的同一种商品,甲用2400元购买的商品数量比乙用3000元购买的商品数量少10件.(1)、求这种商品的单价;(2)、甲,乙两人第二次再去采购该商品时,单价比上次少了20元/件,甲购买商品的总价与上次相同,乙购买商品的数量与上次相同,则甲两次购买这种商品的平均单价是元/件,乙两次购买这种商品的平均单价是元/件.(3)、生活中,无论油价如何变化,有人总按相同金额加油,有人总按相同油量加油,结合(2)的计算结果,建议按相同加油更合算(填“金额”或“油量”).19. 为了提高农副产品的国际竞争力,我国一些行业协会对农副产品的规格进行了划分、某外贸公司要出口一批规格为 的鸡腿,现有两个厂家提供货源,它们的价格相同,鸡腿的品质相近质检员分别从两厂的产品中抽样调查了20只鸡腿,它们的质量(单位: )如下:甲厂:76,74,74,76,73,76,76,77,78,74,76,70,76,76,73,70,77,79,78,71;
甲厂鸡腿质量频数统计表
质量 ( )
频数
频率
2
0.1
3
0.15
10
5
0.25
合计
20
1
乙厂:75,76,77,77,78,77,76,71,74,75,79,71,72,74,73,74,70,79,75,77;
乙厂鸡腿质量频数分布直方图

分析上述数据,得到下表:
统计量
厂家
平均数
中位数
众数
方差
甲厂
75
76
6.3
乙厂
75
75
77
6.6
请你根据图表中的信息完成下列问题:
(1)、 , ;(2)、补全频数分布直方图;(3)、如果只考虑出口鸡腿规格,请结合表中的某个统计量,为外贸公司选购鸡腿提供参考建议;(4)、某外贸公司从甲厂采购了20000只鸡腿,并将质量(单位: )在 的鸡腿加工成优等品,请估计可以加工成优等品的鸡腿有多少只?20. 图1是疫情期间测温员用“额温枪”对小红测温时的实景图,图2是其侧面示意图,其中枪柄 与手臂 始终在同一直线上,枪身 与额头保持垂直量得胳膊 , ,肘关节 与枪身端点 之间的水平宽度为 (即 的长度),枪身 .
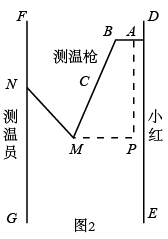
图1
(参考数据: , , , )
(1)、求 的度数;(2)、测温时规定枪身端点 与额头距离范围为 .在图2中,若测得 ,小红与测温员之间距离为 问此时枪身端点 与小红额头的距离是否在规定范围内?并说明理由.(结果保留小数点后一位)21. 如图1,四边形 内接于 , 为直径,过点 作 于点 ,连接 .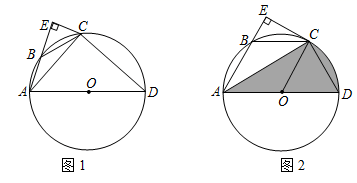 (1)、求证: ;(2)、若 是 的切线, ,连接 ,如图2.
(1)、求证: ;(2)、若 是 的切线, ,连接 ,如图2.①请判断四边形ABCO的形状,并说明理由;
②当AB=2时,求AD , AC与 围成阴影部分的面积.
22. 二次函数 的图象交 轴于原点 及点 .
感知特例
(1)、当 时,如图1,抛物线 上的点 , , , , 分别关于点 中心对称的点为 , , , , ,如下表:…
( ▲ , ▲ )
…
…
…
①补全表格;
②在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为 .
形成概念
我们发现形如(1)中的图象 上的点和抛物线 上的点关于点 中心对称,则称 是 的“孔像抛物线”.例如,当 时,图2中的抛物线 是抛物线 的“孔像抛物线”.
(2)、探究问题①当 时,若抛物线 与它的“孔像抛物线” 的函数值都随着 的增大而减小,则 的取值范围为 ▲ ;
②在同一平面直角坐标系中,当 取不同值时,通过画图发现存在一条抛物线与二次函数 的所有“孔像抛物线” ,都有唯一交点,这条抛物线的解析式可能是 ▲ .(填“ ”或“ ”或“ ”或“ ”,其中 );
③若二次函数 及它的“孔像抛物线”与直线 有且只有三个交点,求 的值.
23. 如图
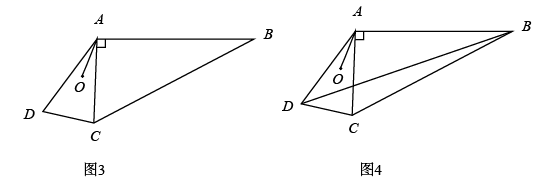 (1)、课本再现
(1)、课本再现在证明“三角形内角和定理”时,小明只撕下三角形纸片的一个角拼成图1即可证明,其中与 相等的角是;
(2)、类比迁移如图2,在四边形 中, 与 互余,小明发现四边形 中这对互余的角可类比(1)中思路进行拼合:先作 ,再过点 作 于点 ,连接 ,发现 , , 之间的数量关系是;
(3)、方法运用如图3,在四边形 中,连接 , ,点 是 两边垂直平分线的交点,连接 , .
①求证: ;
②连接 ,如图4,已知 , , ,求 的长(用含 , 的式子表示).