青海省中考数学真题汇编(近几年)5 图形的变换
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 如图所示的几何体的左视图是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 2. 将一张四条边都相等的四边形纸片按下图中①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应是( )
2. 将一张四条边都相等的四边形纸片按下图中①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应是( )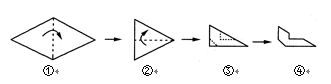 A、
A、 B、
B、 C、
C、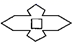 D、
D、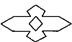 3. 在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟共有( )
3. 在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟共有( )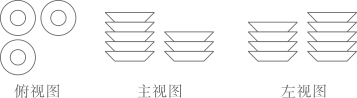 A、4个 B、8个 C、12个 D、17个4. 下面几何体中,俯视图为三角形的是( )A、
A、4个 B、8个 C、12个 D、17个4. 下面几何体中,俯视图为三角形的是( )A、 B、
B、 C、
C、 D、
D、 5. 由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )
5. 由一些相同的小立方块搭成的几何体的三视图如图所示,则搭成该几何体的小立方块有( )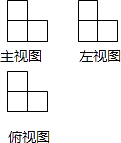 A、3块 B、4块 C、6块 D、9块6. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )
A、3块 B、4块 C、6块 D、9块6. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )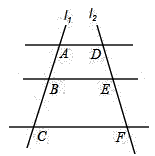 A、3.6 B、4.8 C、5 D、5,27. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )
A、3.6 B、4.8 C、5 D、5,27. 如图,把直角三角形ABO放置在平面直角坐标系中,已知 ,B点的坐标为 ,将 沿着斜边AB翻折后得到 ,则点C的坐标是( )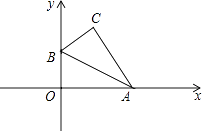 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 如图,将周长为8的 沿BC边向右平移2个单位,得到 ,则四边形 的周长为.
 9. 如图,在直角坐标系中,已知点 ,将 绕点 逆时针方向旋转 后得到 ,则点 的坐标是.
9. 如图,在直角坐标系中,已知点 ,将 绕点 逆时针方向旋转 后得到 ,则点 的坐标是.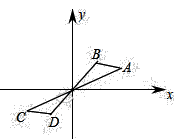 10. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 .
10. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 .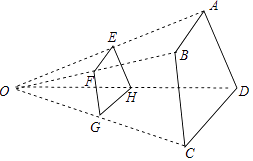 11. 如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据: 米, 米, , ,则 的长为米.(结果保留根号)
11. 如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据: 米, 米, , ,则 的长为米.(结果保留根号)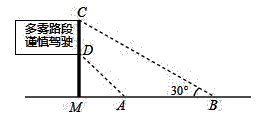 12. 如图是用杠杆撬石头的示意图, 是支点,当用力压杠杆的 端时,杠杆绕 点转动,另一端 向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的 端必须向上翘起 ,已知杠杆的动力臂 与阻力臂 之比为 ,要使这块石头滚动,至少要将杠杆的 端向下压 .
12. 如图是用杠杆撬石头的示意图, 是支点,当用力压杠杆的 端时,杠杆绕 点转动,另一端 向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的 端必须向上翘起 ,已知杠杆的动力臂 与阻力臂 之比为 ,要使这块石头滚动,至少要将杠杆的 端向下压 . 13. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连接AD,若 ,则 .
13. 如图,将 绕直角顶点C顺时针旋转 ,得到 ,连接AD,若 ,则 . 14. 在 中,若 ,则 的度数是 .
14. 在 中,若 ,则 的度数是 .
15. 如图所示的图案由三个叶片组成,绕点O旋转120°后可以和自身重合,若每个叶片的面积为4cm2 , ∠AOB=120°,则图中阴影部分的面积为 .
三、计算题
-
16. 计算:
17. 计算:18. 计算:四、解答题
-
19. 如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ),将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据 , , ).
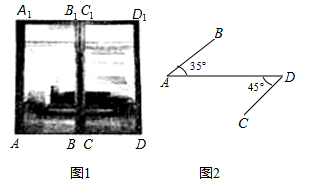 20. 某市为了加快5G网络信号覆盖,在市区附近小山顶架设信号发射塔,如图所示.小军为了知道发射塔的高度,从地面上的一点A测得发射塔顶端P点的仰角是45°,向前走60米到达B点测得P点的仰角是60°,测得发射塔底部Q点的仰角是30°.请你帮小军计算出信号发射塔PQ的高度.(结果精确到0.1 米, )
20. 某市为了加快5G网络信号覆盖,在市区附近小山顶架设信号发射塔,如图所示.小军为了知道发射塔的高度,从地面上的一点A测得发射塔顶端P点的仰角是45°,向前走60米到达B点测得P点的仰角是60°,测得发射塔底部Q点的仰角是30°.请你帮小军计算出信号发射塔PQ的高度.(结果精确到0.1 米, )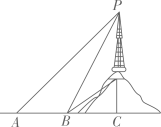 21. 如图,同学们利用所学知识去测量三江源某河段某处的宽度 小宇同学在A处观测对岸点C,测得 ,小英同学在距点A处60米远的B点测得 ,请根据这些数据算出河宽 精确到 米, , .
21. 如图,同学们利用所学知识去测量三江源某河段某处的宽度 小宇同学在A处观测对岸点C,测得 ,小英同学在距点A处60米远的B点测得 ,请根据这些数据算出河宽 精确到 米, , .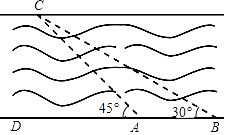
五、综合题
-
22. 如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过点 作 于点 ,交 的延长线于点 ,过点 作 于点 .
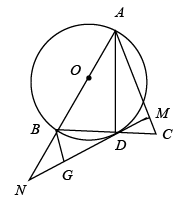 (1)、求证: ;(2)、求证:直线 是 的切线.23. 在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作 等大小的角,可以采用如下方法:
(1)、求证: ;(2)、求证:直线 是 的切线.23. 在我们学习过的数学教科书中,有一个数学活动,若身旁没有量角器或三角尺,又需要作 等大小的角,可以采用如下方法:
操作感知:
第一步:对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开(如图13-1).
第二步:再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 (如图13-2).
(1)、猜想论证:
若延长 交 于点 ,如图13-3所示,试判定 的形状,并证明你的结论.(2)、拓展探究:
在图13-3中,若 ,当 满足什么关系时,才能在矩形纸片 中剪出符(1)中的等边三角形 ?24. 如图,在 中,点 、 分别是半径 、弦 的中点,过点 作 于点 .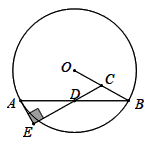 (1)、求证: 是 的切线;(2)、若 , ,求 的半径.25. 如图,抛物线 与坐标轴交点分别为 , , ,作直线BC.
(1)、求证: 是 的切线;(2)、若 , ,求 的半径.25. 如图,抛物线 与坐标轴交点分别为 , , ,作直线BC.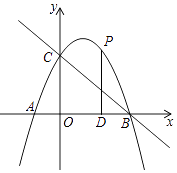 (1)、求抛物线的解析式;(2)、点P为抛物线上第一象限内一动点,过点P作 轴于点D,设点P的横坐标为 ,求 的面积S与t的函数关系式;(3)、条件同 ,若 与 相似,求点P的坐标.26. 请认真阅读下面的数学小探究系列,完成所提出的问题:
(1)、求抛物线的解析式;(2)、点P为抛物线上第一象限内一动点,过点P作 轴于点D,设点P的横坐标为 ,求 的面积S与t的函数关系式;(3)、条件同 ,若 与 相似,求点P的坐标.26. 请认真阅读下面的数学小探究系列,完成所提出的问题: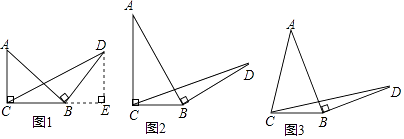 (1)、探究1:如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 求证: 的面积为 提示:过点D作BC边上的高DE,可证 ≌
(1)、探究1:如图1,在等腰直角三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 求证: 的面积为 提示:过点D作BC边上的高DE,可证 ≌
(2)、探究2:如图2,在一般的 中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 请用含a的式子表示 的面积,并说明理由.
(3)、探究3:如图3,在等腰三角形ABC中, , ,将边AB绕点B顺时针旋转 得到线段BD,连接 试探究用含a的式子表示 的面积,要有探究过程.