青海省中考数学真题汇编(近几年)4 图形的性质
试卷更新日期:2021-08-20 类型:二轮复习
一、单选题
-
1. 如图是一个废弃的扇形统计图,小明同学利用它的阴影部分制作一个圆锥,则这个圆锥的底面半径是( )
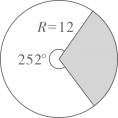 A、3.6 B、1.8 C、3 D、62. 将一张四条边都相等的四边形纸片按下图中①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应是( )
A、3.6 B、1.8 C、3 D、62. 将一张四条边都相等的四边形纸片按下图中①②的方式沿虚线依次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应是( )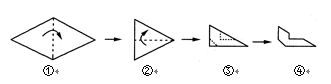 A、
A、 B、
B、 C、
C、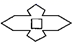 D、
D、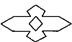 3. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于 , 两点,他测得“图上”圆的半径为10厘米, 厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
3. 如图是一位同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于 , 两点,他测得“图上”圆的半径为10厘米, 厘米.若从目前太阳所处位置到太阳完全跳出海平面的时间为16分钟,则“图上”太阳升起的速度为( ). A、1.0厘米/分 B、0.8厘米分 C、12厘米/分 D、1.4厘米/分4. 已知 , 是等腰三角形的两边长,且a,b满足 ,则此等腰三角形的周长为( ).A、8 B、6或8 C、7 D、7或85. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A、55°,55° B、70°,40°或70°,55° C、70°,40° D、55°,55°或70°,40°6. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放:两个三角板的一直角边重合,含 角的三角板的斜边与纸条一边重合,含 角的三角板的一个顶点在纸条的另一边上,则 的度数是( )
A、1.0厘米/分 B、0.8厘米分 C、12厘米/分 D、1.4厘米/分4. 已知 , 是等腰三角形的两边长,且a,b满足 ,则此等腰三角形的周长为( ).A、8 B、6或8 C、7 D、7或85. 等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A、55°,55° B、70°,40°或70°,55° C、70°,40° D、55°,55°或70°,40°6. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放:两个三角板的一直角边重合,含 角的三角板的斜边与纸条一边重合,含 角的三角板的一个顶点在纸条的另一边上,则 的度数是( )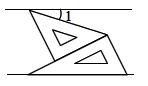 A、 B、 C、 D、7. 如图,小莉从 点出发,沿直线前进10米后左转 ,再沿直线前进10米,又向左转 , ,照这样走下去,她第一次回到出发点 时,一共走的路程是( )
A、 B、 C、 D、7. 如图,小莉从 点出发,沿直线前进10米后左转 ,再沿直线前进10米,又向左转 , ,照这样走下去,她第一次回到出发点 时,一共走的路程是( )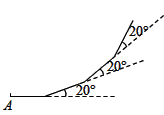 A、150米 B、160米 C、180米 D、200米8. 如图,在扇形 中, 为弦, , , ,则 的长为( )
A、150米 B、160米 C、180米 D、200米8. 如图,在扇形 中, 为弦, , , ,则 的长为( )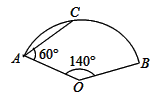 A、 B、 C、 D、9. 根据图中给出的信息,可得正确的方程是( )
A、 B、 C、 D、9. 根据图中给出的信息,可得正确的方程是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 如图所示ΔABC中,AB=AC=14cm,AB的垂直平分线MN交AC于D,ΔDBC的周长是24cm,则BC=cm.
 11. 点 是非圆上一点,若点 到 上的点的最小距离是 ,最大距离是 ,则 的半径是 .12. 如图,在 中, , , 分别是边 , , 的中点,若 的周长为10,则 的周长为 .
11. 点 是非圆上一点,若点 到 上的点的最小距离是 ,最大距离是 ,则 的半径是 .12. 如图,在 中, , , 分别是边 , , 的中点,若 的周长为10,则 的周长为 .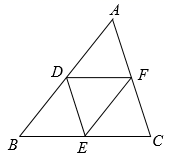 13. 如图,在 中,对角线 , ,垂足为 ,且 , ,则 与 之间的距离为 .
13. 如图,在 中,对角线 , ,垂足为 ,且 , ,则 与 之间的距离为 .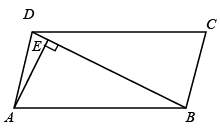 14. 已知⊙O的直径为10cm,AB,CD是⊙O的两条弦, , , ,则 与 之间的距离为cm.15. 如图,在矩形 中,对角线 , 相交于点O,已知 , ,则 的长为cm.
14. 已知⊙O的直径为10cm,AB,CD是⊙O的两条弦, , , ,则 与 之间的距离为cm.15. 如图,在矩形 中,对角线 , 相交于点O,已知 , ,则 的长为cm.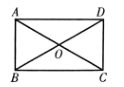 16. 已知a,b,c为 的三边长.b,c满足 ,且a为方程 的解,则 的形状为三角形.17. 在 中, , , ,则 的内切圆的半径为.18. 如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据: 米, 米, , ,则 的长为米.(结果保留根号)
16. 已知a,b,c为 的三边长.b,c满足 ,且a为方程 的解,则 的形状为三角形.17. 在 中, , , ,则 的内切圆的半径为.18. 如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据: 米, 米, , ,则 的长为米.(结果保留根号)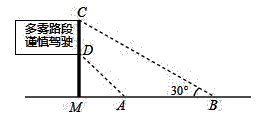 19. 如图在正方形 中,点 是以 为直径的半圆与对角线 的交点,若圆的半径等于1,则图中阴影部分的面积为.
19. 如图在正方形 中,点 是以 为直径的半圆与对角线 的交点,若圆的半径等于1,则图中阴影部分的面积为.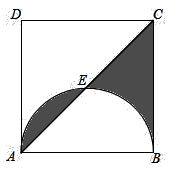
三、解答题
-
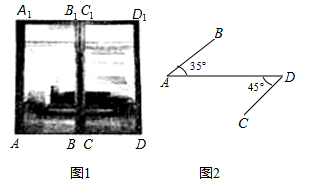
20. 如图1是某中学教学楼的推拉门,已知门的宽度 米,且两扇门的大小相同(即 ),将左边的门 绕门轴 向里面旋转 ,将右边的门 绕门轴 向外面旋转 ,其示意图如图2,求此时 与 之间的距离(结果保留一位小数).(参考数据 , , ).
四、作图题
-
21. 如图,在 中, .
 (1)、尺规作图:作 的外接圆 ;作 的角平分线交 于点D,连接AD.(不写作法,保留作图痕迹)(2)、若AC =6,BC =8,求AD的长.
(1)、尺规作图:作 的外接圆 ;作 的角平分线交 于点D,连接AD.(不写作法,保留作图痕迹)(2)、若AC =6,BC =8,求AD的长.五、综合题
-
22. 如图, 是 的对角线.
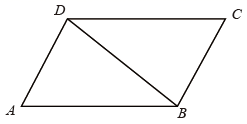 (1)、尺规作图(请用2B铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).(2)、试判断四边形 的形状并说明理由.23. 如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过点 作 于点 ,交 的延长线于点 ,过点 作 于点 .
(1)、尺规作图(请用2B铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).(2)、试判断四边形 的形状并说明理由.23. 如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过点 作 于点 ,交 的延长线于点 ,过点 作 于点 .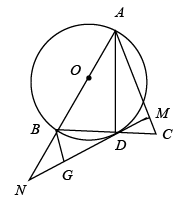 (1)、求证: ;(2)、求证:直线 是 的切线.24. 如图,已知AB是 的直径,直线BC与 相切于点B,过点A作AD//OC交 于点D,连接CD.
(1)、求证: ;(2)、求证:直线 是 的切线.24. 如图,已知AB是 的直径,直线BC与 相切于点B,过点A作AD//OC交 于点D,连接CD.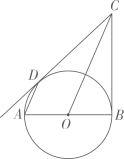 (1)、求证:CD是 的切线.(2)、若 ,直径 ,求线段BC的长.25. 如图,在 中, , 是 的中点, 是 的中点,过点 作 交 的延长线于点 ,连接 .
(1)、求证:CD是 的切线.(2)、若 ,直径 ,求线段BC的长.25. 如图,在 中, , 是 的中点, 是 的中点,过点 作 交 的延长线于点 ,连接 .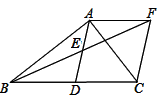 (1)、求证: ;(2)、证明四边形 是菱形.26. 如图,在 中,点 、 分别是半径 、弦 的中点,过点 作 于点 .
(1)、求证: ;(2)、证明四边形 是菱形.26. 如图,在 中,点 、 分别是半径 、弦 的中点,过点 作 于点 .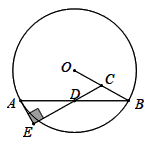 (1)、求证: 是 的切线;(2)、若 , ,求 的半径.27. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①
(1)、求证: 是 的切线;(2)、若 , ,求 的半径.27. 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”,三斜即指三角形的三条边长,可以用该方法求三角形面积.若改用现代数学语言表示,其形式为:设 , , 为三角形三边, 为面积,则 ①这是中国古代数学的瑰宝之一.
而在文明古国古希腊,也有一个数学家海伦给出了求三角形面积的另一个公式,若设 (周长的一半),则 ②
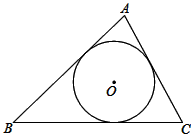 (1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .28. 在 中, , 交BA的延长线于点G.
(1)、尝试验证.这两个公式在表面上形式很不一致,请你用以5,7,8为三边构成的三角形,分别验证它们的面积值;(2)、问题探究.经过验证,你发现公式①和②等价吗?若等价,请给出一个一般性推导过程(可以从① ②或者② ① ;(3)、问题引申.三角形的面积是数学中非常重要的一个几何度量值,很多数学家给出了不同形式的计算公式.请你证明如下这个公式:如图, 的内切圆半径为 ,三角形三边长为 , , ,仍记 , 为三角形面积,则 .28. 在 中, , 交BA的延长线于点G.特例感知:
(1)、将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC重合,另一条直角边恰好经过点B.通过观察、测量BF与CG的长度,得到 .请给予证明.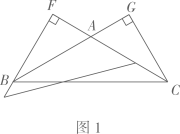 (2)、当三角尺沿AC方向移动到图2所示的位置时,一条直角边仍与AC边重合,另一条直角边交BC于点D,过点D作 垂足为E.此时请你通过观察、测量DE,DF与CG的长度,猜想并写出DE、DF与CG之间存在的数量关系,并证明你的猜想.
(2)、当三角尺沿AC方向移动到图2所示的位置时,一条直角边仍与AC边重合,另一条直角边交BC于点D,过点D作 垂足为E.此时请你通过观察、测量DE,DF与CG的长度,猜想并写出DE、DF与CG之间存在的数量关系,并证明你的猜想.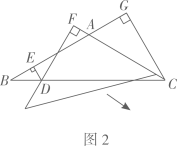 (3)、当三角尺在图2的基础上沿AC方向继续移动到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
(3)、当三角尺在图2的基础上沿AC方向继续移动到图3所示的位置(点F在线段AC上,且点F与点C不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)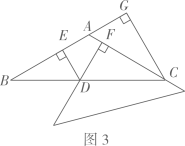
-
-